
- •ВВЕДЕНИЕ
- •1.2. Операции над матрицами
- •1.3. Определители и их вычисление
- •1.5. Обратная матрица
- •1.6. Ранг матрицы и способы его вычисления
- •2. ЛИНЕЙНЫЕ ПРОСТРАНСТВА
- •3.1. Основные определения
- •3.2. Матричный способ решения СЛАУ
- •3.3. Решение СЛАУ по формулам Крамера
- •3.4. Основные теоремы об общем решении СЛАУ
- •3.5. Метод Жордана – Гаусса решения стандартной СЛАУ
- •4. ВЕКТОРНАЯ АЛГЕБРА
- •4.1. Линейные операции над векторами
- •4.2. Скалярное произведение векторов
- •4.3. Векторное произведение векторов
- •4.4. Смешанное произведение векторов
- •5. ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
- •5.1. Метод координат
- •5.2. Прямая на плоскости
- •5.3. Плоскость
- •5.4. Прямая в пространстве
- •6. КОМПЛЕКСНЫЕ ЧИСЛА
- •7. АЛГЕБРА МНОГОЧЛЕНОВ
- •ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
- •СПИСОК ЛИТЕРАТУРЫ
4.ВЕКТОРНАЯ АЛГЕБРА
4.1.Линейные операции над векторами
Свободным вектором называется направленный отрезок, который можно перемещать в пространстве без изменения его длины и направления. В данной главе свободные векторы будем называть просто векторами. Векторы обозначаются либо малыми латинскими буквами, выделенными жирным шрифтом, либо упорядоченной парой точек его начала и конца, запи-
санной под общей чертой. На рис. 1 изображен вектор
|
a |
В |
|
|
|
|
|
|
|
a AB, |
конец вектора указан стрелкой. Длина вектора а на- |
||||||||
А |
|||||||||
|
|
||||||||
|
|
|
|
|
|
|
|
||
|
Рис. 1 |
|
зывается его модулем и обозначается |
a |
. Нулевым называет- |
||||
|
|
|
|
|
|
|
|
||
ся вектор, начало и конец которого совпадают. Нулевой вектор обозначается символом 0 , модуль нулевого вектора равен нулю.
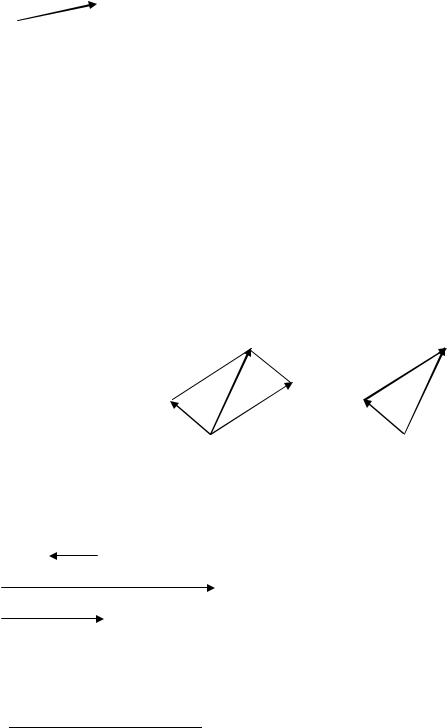
В множестве векторов вводятся линейные операции сложения и умножения на число. Сумму двух векторов можно определить двумя равносильными способами: по правилу параллелограмма и по правилу треугольника.
Правило параллелограмма (рис. 2): векторы-слагаемые откладывают от общего начала, их суммой называется вектор, начало которого совпадает с общим началом векторов-слагаемых, а конец с противоположной вершиной параллелограмма, построенного на этих векторах, как на ребрах.
Правило треугольника (рис. 3): отложим векторы-слагаемые так, чтобы начало второго совпадало с концом первого; тогда их суммой называется вектор, начало которого совпадает с началом первого, а конец – с концом второго вектора.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
a b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a b |
|
b |
a |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Рис. 2 |
|
|
|
|
|
|
|
|
|
Рис. 3 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
Векторы, параллельные одной прямой, называются коллинеарными. |
||||||||||||||||||
Нулевой вектор 0 по определению коллинеарен любому вектору. |
|
|||||||||||||||||
|
Произведением вектора a на число (рис. 4) |
|||||||||||||||||
0,5a |
называется новый вектор b a , который удов- |
|||||||||||||||||
2a |
летворяет следующим трем условиям: |
|
||||||||||||||||
1) |
|
b |
|
|
|
a |
|
|
|
|
|
|
|
a |
|
;7) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
a |
2) b a коллинеарен вектору а; |
|
||||||||||||||||
Рис. 4 |
3) b a |
|
сонаправлен а, если 0 |
и a 0 ; |
||||||||||||||
|
направлен противоположно a, если 0 |
и a 0 . |
||||||||||||||||
7) Отсюда следует, что если a 0 и/или 0 , то b a 0 .
44
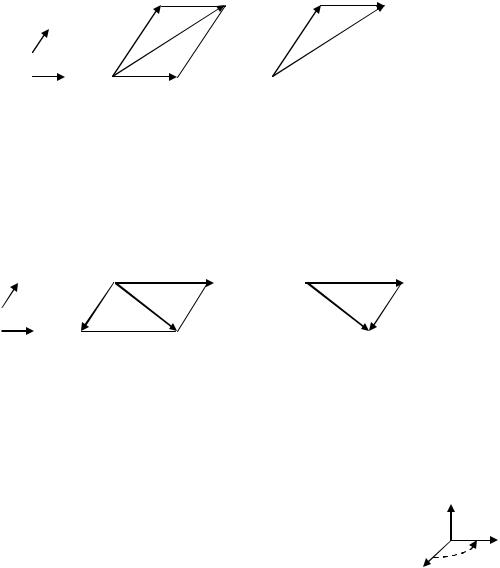
Пример 1. Графически даны два вектора а и b (рис. 5, 6), графически построить векторы 2a 3b и 3a 2b по правилу параллелограмма и по правилу треугольника.
Решение. 1) Строим вектор 2а, увеличивая длину а в два раза и сохраняя направление вектора а. Строим вектор 3b, увеличивая длину b в три раза и сохраняя направление вектора b. Откладываем векторы 2а и 3b от одного начала и строим параллелограмм на векторах 2а и 3b как на ребрах. Проводим вектор 2a 3b из общего начала векторов 2а и 3b в противоположную вершину параллелограмма (рис. 5).
2) Строим векторы 2а и вектор 3b. Параллельным переносом совмещаем конец вектора 3b и начало вектора 2а. Проводим вектор 2a 3b из начала вектора 3b в конец вектора 2а (рис. 5). Заметим, что 2a 3b 3b 2a .
|
|
2a |
|
b |
3b |
3b |
|
2a 3b |
2a 3b |
||
|
|||
a |
2a |
|
|
|
Рис. 5 |
|
3) Строим вектор 3а, увеличивая длину а в три раза и сохраняя направление вектора а. Строим вектор –2b, увеличивая длину b в два раза и изменяя направление вектора b на противоположное. Откладываем векторы 3а и –2b от одного начала и строим параллелограмм на векторах 3а и –2b, как на ребрах. Проводим вектор 3а – 2b из общего начала векторов 3а и –2b в противоположную вершину параллелограмма (рис. 6).
|
|
|
3a |
3a |
b |
2b |
|
3a 2b |
2b |
|
3a 2b |
|||
|
|
|||
|
|
|
|
|
|
a |
|
|
|
|
|
|
Рис. 6 |
|
4) Строим векторы 3а и –2b. Параллельным переносом совмещаем конец вектора 3а и начало вектора –2b. Проводим вектор 3а – 2b из начала вектора 2а в конец вектора 3b (рис. 6).
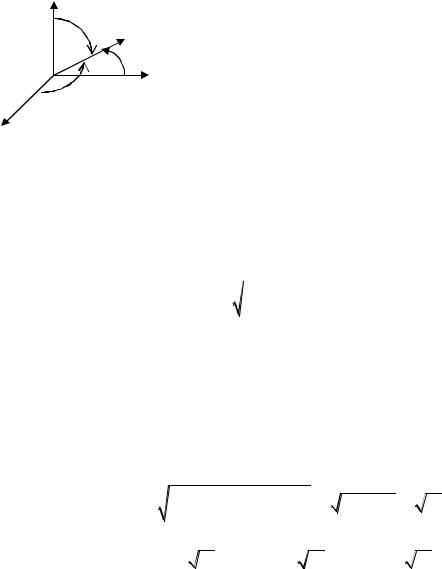
Ортом называется вектор, модуль которого равен единице. Упорядоченная тройка векторов i, j, k , отложенных от
общего начала, называется правой, если кратчайший пово- |
|
|
рот от первого вектора ко второму, наблюдаемый из конца |
j |
|
третьего вектора, виден как совершающийся против часовой |
||
|
||
стрелки (рис. 7). |
i |
Известно [1], что множество векторов является линейным пространством размерности три. Обозначим через i, j, k
правую тройку трех взаимно перпендикулярных ортов (рис. 7). Векторы i, j, k образуют базис линейного пространства векторов, любой вектор а можно
45
разложить по базису i, j, k, т. е. представить в виде a axi ay j az k , где ax , ay , az – числовые коэффициенты, называемые координатами вектора a
в базисе i, j, k.
Любой вектор однозначно определяется тройкой своих координат, поэтому в дальнейшем будем использовать запись a ax , ay , az , отождеств-
ляя вектор с упорядоченной тройкой его координат. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
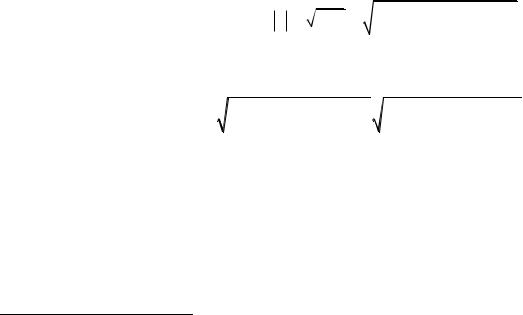
Углы , |
|
|
, |
(рис. 8) между данным векто- |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ром a и ортами базиса i, j, k называются направ- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ляющими углами вектора a, а косинусы этих углов |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
a |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
cos , cos , cos |
– |
направляющими косинусами |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
j |
вектора a. Направляющие косинусы определяют |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
направление вектора, а длину вектора задает его |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
i |
|
|
|
|
модуль. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Зная модуль вектора и его направляющие ко- |
|||||||||||||||||||||||||||||||||||||||||
Рис. 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
синусы, можно найти его координаты |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
ax |
|
a |
|
|
cos , |
ay |
|
a |
|
cos , |
az |
|
|
a |
|
|
cos . |
(1) |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
В свою очередь, зная координаты ax , |
|
ay , |
az |
вектора a, можно найти его |
|||||||||||||||||||||||||||||||||||||||||||||||||||
модуль и направляющие косинусы по формулам |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
ax 2 ay 2 |
az 2 , |
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
cos |
|
a |
x |
|
|
, |
cos |
ay |
|
, |
|
cos |
a |
z |
|
|
. |
|
|
|
|
(3) |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
a |
|
|
|
|
a |
|
|
|
a |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Пример 2. Дано разложение вектора |
a 2i 3 j k |
по базису i, j, k. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
Найти модуль и направляющие косинусы вектора a. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Решение. Координаты вектора а равны ax 2 , |
ay 3 , |
az 1 (это коэф- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
фициенты при ортах i, j, k в разложении вектора а). По формулам (2, 3) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
ax 2 ay 2 az 2 |
|
|
|
|
|
; |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
a |
4 9 1 |
14 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
cos |
2 |
|
|
|
, |
|
|
|
cos |
|
|
|
3 |
|
|
, |
|
|
cos |
|
1 |
|
. |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|||||||||||||||||||
|
a |
|
5 и его направляющие косинусы |
||||||||||||||||||||||||||||||||||||||||||||||||||||
Пример 3. Даны модуль вектора |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
3 |
, |
cos |
4 |
|
, cos 0 , найти его координаты и разложение по базису |
||||||||||||||
|
|
|
|
|||||||||||||||||
|
5 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
i, j, k. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. По формуле (1) |
|
|
5 2 2 , a |
|
|
|
|
|||||||||||||
|
|
|
a |
x |
|
|
a |
|
cos 5 |
3 |
|
3 , a |
y |
z |
5 |
0 |
0 ; |
|||
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
5 |
|
|
5 |
5 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
a axi ay j az k 3i 2 j 0k 3i 2 j.
46
4.2. Скалярное произведение векторов
Скалярным произведением векторов a ax , ay , az и b bx ,by ,bz называется число, обозначаемое ab и определяемое формулой
ab axbx ayby azbz . |
|
(4) |
Пример 4. Найти скалярное произведение векторов |
a 2, |
3, 1 и |
b 0, 1, 3 . |
|
|
Решение. По формуле (4) |
|
|
ab axbx ayby azbz 2 0 3 1 1 3 6 .
Если хотя бы один из векторов a, b равен 0, то скалярное произведение ab равно нулю. Если оба вектора не равны 0, то
|
|
|
|
|
|
|
|
|
ab |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
b |
|
cos a,b |
. |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 и угол между |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Пример 5. Даны модули двух векторов |
|
a |
|
и |
|
b |
|
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||
ними |
|
, найти скалярное произведение ab. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. По формуле (5) |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
ab |
a |
|
|
|
b |
|
cos a, b 1 2 cos |
|
2 |
|
1. |
||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Применение скалярного произведения
1)Модуль вектора a равен: a 
 a a
a a 
 ax 2 ay 2 az 2 .
ax 2 ay 2 az 2 .
2)Косинус угла между векторами a, b равен
|
|
|
|
|
ab |
|
|
|
|
|
axbx ayby azbz |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
cos a, b |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
a |
|
b |
|
|
ax |
2 |
ay |
2 |
az |
2 |
bx |
2 |
by |
2 |
bz |
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
3)Признак перпендикулярности векторов: векторы a, b перпенди-
кулярны8) тогда и только тогда, когда ab 0 .
4)Признак параллельности векторов: векторы a, b параллельны то-
гда и только тогда, когда
a |
x |
|
ay |
|
a |
z |
9) |
(5) |
|
|
|
|
. |
||||||
bx |
by |
bz |
|||||||
|
|
|
|
||||||
8)По определению полагают, что нулевой вектор перпендикулярен любому вектору.
9)Равенство (5) означает пропорциональность координат двух векторов, поэтому, если знаменатель какой-либо дроби равен нулю, то для выполнения (5) и числитель этой дроби также должен быть равен нулю.
47
5) Проекция вектора a на направление вектора b равна
|
Пр |
a |
ab |
|
|
axbx |
ayby |
azbz |
|
|
|
. |
|
(6) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
b |
|
|
b |
|
|
bx |
2 |
by |
2 |
bz |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
a 2, |
0, 1 и |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Пример 6. Найти косинус |
угла |
|
между векторами |
|||||||||||||||
b 0, 1, |
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ab |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
axbx ayby azbz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Решение. cos a, b = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
b |
|
|
|
|
ax |
2 |
ay |
2 |
|
az |
2 |
|
bx |
2 |
by |
2 |
bz |
2 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 . |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0 0 |
|
|
1 |
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2 0 2 1 2 |
0 2 1 2 2 2 |
|
|
|
|
|
5 5 5 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пример 7. Какие из следующих векторов параллельны, а какие перпен- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
дикулярны друг другу a 2, 0, 1 , |
|
b 0, 1, 2 , с 1, 7, 2 , d 4, 0, 2 ? |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Решение. Вычисляем скалярные произведения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ab 2, 0, 1 0, 1, 2 2 0 , |
|
|
|
|
|
aс 2, 0, 1 1, 7, 2 0 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ad 2, 0, 1 4, 0, 2 10 0 , |
|
|
|
|
|
bс 0, 1, 2 1, 7, 2 3 0 , |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
bd 0, 1, 2 4, 0, 2 4 0 , |
|
|
|
|
|
cd 1, 7, 2 4, 0, 2 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
По признаку перпендикулярности a с , с d . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Проверяем выполнение соотношения (5): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
для a,b |
|
|
2 |
|
|
0 |
|
|
|
|
1 , |
|
|
|
|
|
|
|
для |
|
a,с |
2 |
|
0 |
|
|
|
1 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
7 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
для a, d |
|
2 |
|
|
|
|
0 |
|
|
1 |
, |
|
|
|
|
|
|
|
для |
|
b,с |
0 |
|
|
1 |
2 |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
7 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
для b, d |
|
0 |
|
|
|
|
1 |
|
2 |
, |
|
|
|
|
|
|
|
для |
|
с, d |
|
1 |
|
|
|
|
7 |
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
По признаку параллельности векторов a || d . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пример 8. Найти проекцию вектора a 2, 1, 1 |
на направление векто- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ра b 1, 1, |
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Решение. По формуле (6) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
Пр |
a |
|
ab |
|
|
|
|
|
|
|
axbx ayby azbz |
|
|
|
|
|
|
2 1 1 1 1 2 |
|
|
|
|
1 |
|
. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
b |
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
bx |
|
2 |
by |
2 |
bz |
|
2 |
|
|
|
|
|
|
|
1 |
2 |
1 |
2 |
|
2 |
2 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Пример 9. Найти |
|
p |
, если p |
2a 3b , |
|
|
a |
|
|
1, |
|
|
b |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
и cos a,b |
3 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2a 3b 2a 3b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Решение. |
p |
|
|
|
p p |
|
|
|
4a a 12a b 9b b |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
9 32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
4 |
a |
12 |
a |
|
b |
cos a,b 9 |
b |
|
|
|
|
4 1 12 1 3 |
97 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
48
