Добавил:

CanyonE СПбГУТ * ИКСС * Программная инженерия Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный университет телекоммуникаций им. проф. М.А. Бонч-Бруевича

Предмет:

Линейная алгебра

Файл:

Ведина О. И., Рабкин Е. Л. Линейная алгебра для экономистов. Практикум.pdf

Скачиваний:

Добавлен:

17.06.2020

Размер:

1.88 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1510 11 12 13 14 15 > Следующая >>>

Расстояние от точки до прямой на плоскости

Расстояние от точки M0 x0 , y0 до прямой Ax By C 0 равно

d	Ax0 By0		C	.
	Ax0 By0		C


		A2 B2
		A2 B2
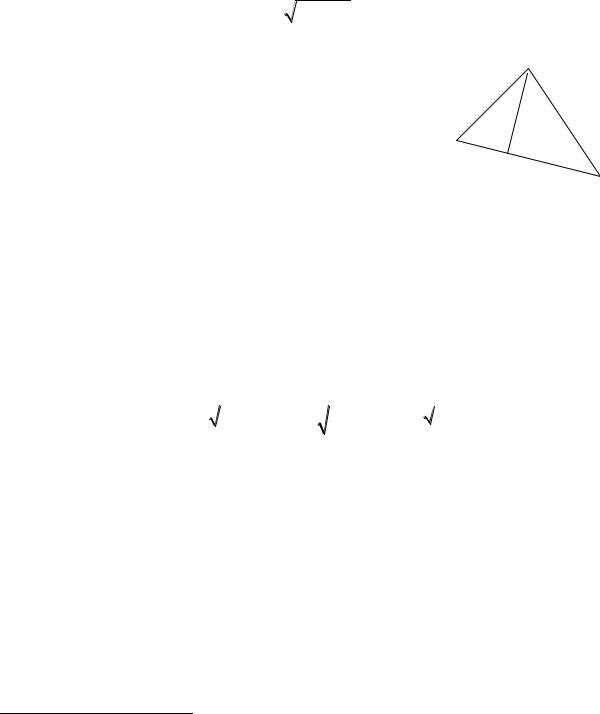
Пример 13. Даны уравнение x 2y 1 0 ос-					B
нования треугольника ABC (рис. 9) и координаты					B
нования треугольника ABC (рис. 9) и координаты
вершины B(1, –4). Составить уравнение высоты
треугольника и найти ее длину.
Решение. Из уравнения x 2y 1 0			прямой		A
AC определяем ее нормаль N(1, –2). Вектор N(1, –2)					A
AC определяем ее нормаль N(1, –2). Вектор N(1, –2)					D
параллелен высоте BD и потому является направ-					D
параллелен высоте BD и потому является направ-					C
ляющим вектором для BD: pBD N 1, 2 . Зная					Рис. 9

точку B(1, –4) на высоте BD и направляющий вектор pBD 1, 2 этой высоты, составляем каноническое уравнение высоты

	x x0			y y0			x 1	y 4			.
											.
		m		n		1			2
Длину высоты можно определить как расстояние от точки B(1, –4)
до прямой AC с уравнением x 2y 1 0
d		Ax0 By0 C			1 2 4 1					10		.



			A2 B2			12 2 2				5
			A2 B2			12 2 2				5

5.3. Плоскость

Нормалью плоскости называется любой ненулевой вектор N A, B,C , ортогональный этой плоскости.

Основные виды уравнения плоскости

1) Общее уравнение плоскости

Ax By Cz D 0 ,

(14)

Здесь вектор N A, B,C – нормаль плоскости13).

13) Если в общем уравнении плоскости: 1) D = 0, то плоскость проходит через начало координат; 2) A = 0, то плоскость параллельна координатной оси Ox; 3) B = 0, то плоскость параллельна координатной оси Oy; 4) C = 0, то плоскость параллельна координатной оси

Oz; 5) A B 0 , то плоскость параллельна координатной плоскости Oxy; 6) A C 0 , то плоскость параллельна координатной плоскости Oxz; 7) C B 0 , то плоскость парал-

лельна координатной плоскости Oyz.

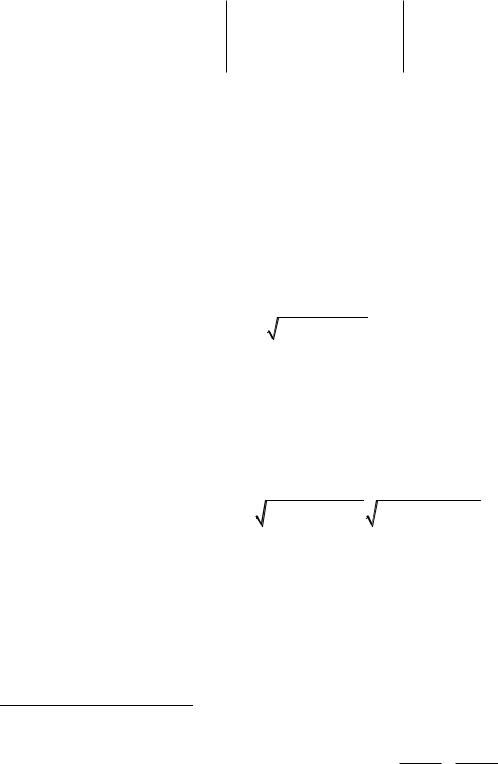
2) Уравнение плоскости, проходящей через точку M0 x0 , y0 , z0 , с нормалью N A, B,C

A x x0 B y y0 С z z0 0 .	(15)
3) Уравнение плоскости, проходящей через точки	M0 x0 , y0 , z0 ,
M1 x1, y1, z1 , M 2 x2 , y2 , z2

x x0 x1 x0 x2 x0

y y0 y1 y0 y2 y0

z z0

z1 z0 0 . (16) z2 z0

4) Уравнение плоскости в отрезках, т. е. плоскости, пересекающей оси

координат соответственно в точках x a ,			y b ,		z c
	x	y	z	1.	(17)
	a	b	c

Расстояние от точки до плоскости

Расстояние от точки

M0 x0 , y0 , z0

до плоскости

Ax By Cx D 0

равно

Ax0 By0 Cz0 D

A2 B2 C2

Взаимное расположение двух плоскостей

Пусть N

A , B ,C ,

A , B ,C – нормали двух плоскостей14), а –

угол между ними, тогда:

1) косинус угла между двумя плоскостями равен

cos

N1 N2

A1 A2 B1B2 C1C2

; .

A 2

B 2 C 2

A 2

B 2 C 2

2) две плоскости параллельны друг другу, если

;

3) две плоскости взаимно перпендикулярны, если

A1 A2 B1B2 C1C2 0 .

14) Если задано общее уравнение плоскости Ax By Cx D 0 , то вектор N(A, B, C) есть нормаль этой плоскости. Если же заданы три точки M 0 x0 , y0 , z0 , M1 x1 , y1 ,z1 , M2 x2 , y2 ,z2 на плоскости, то векторное произведение M0M1 M0M 2 также является нормалью плоскости.

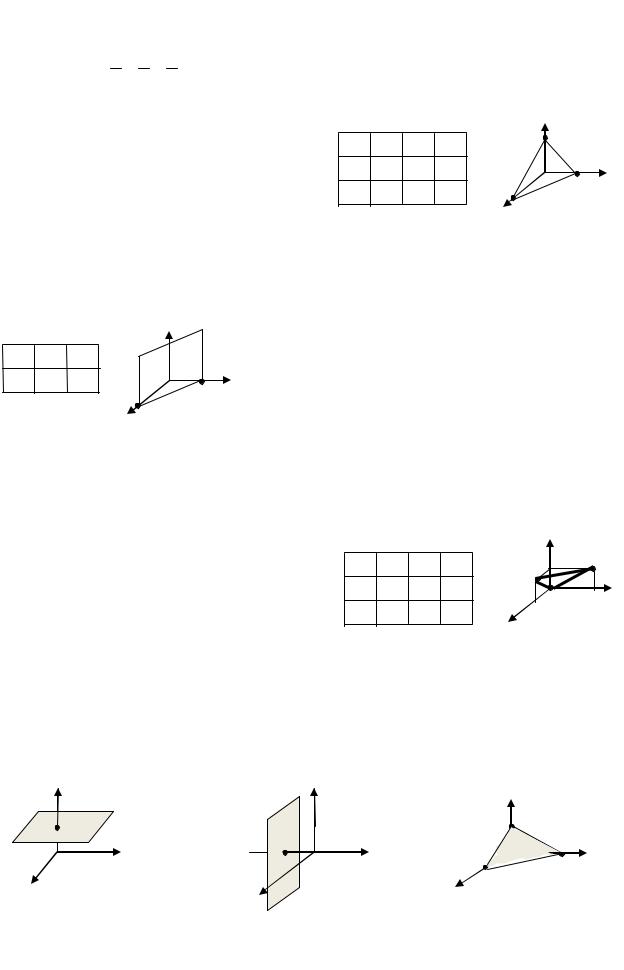
Пример 14. Построить плоскости, заданные своими уравнениями:

а) 2x 3y 2z 6 0 ;

б) 2x 3y 6 0 ;

в) 2x y 2z 0 ;

г) z 2 ;

д) y 1; е) x

Решение. а) Находим точки M0 0,0,3 ,

Таблица 2

M1 0, 2, 0 , M 2 3,0,0

пересечения плос-

кости 2x 3y 2z 6 0 с осями коорди-

нат,

предварительно

составив

таблицу

(табл. 2). Затем

отмечаем

найденные

точки и проводим через них плоскость

Рис. 10

(рис. 10).

б) В уравнении 2x 3y 6 0 коэффициент C при неизвестной z равен

нулю,

поэтому плоскость параллельна оси Oz.

Находим точки

M1 0, 2,0 ,

Таблица 3

M 2 3, 0, 0

пересечения

плоскости

2x 3y 6 0 с осями координат Ox

и Oy,

предварительно

составив

табл.

Затем

отмечаем найденные точки на осях коор-

динат и проводим через них плоскость па-

Рис. 11

раллельно оси Oz (рис. 11).

в) В уравнении 2x + y – 2z = 0 свобод-

ный член D равен нулю, поэтому плоскость проходит через начало коор-

динат. Находим точки M1(1, 0, 1), M2(0, 2, 1) в плоскости 2x y 2z 0 , ле-

жащие в координатных плоскостях Oxz и

Таблица 4

Oyz, предварительно составив табл. 4. За-

тем отмечаем найденные точки и прово-

дим через них и начало координат плос-

кость (рис. 12).

z 2

г) В уравнении

коэффициен-

Рис. 12

ты A, B при неизвестных x, y равны ну-

лю,

поэтому плоскость z 2 параллельна координатной плоскости Oxy,

пересекает координатную ось Oz в точке z 2 (рис. 13).

д) Аналогично пункту г строим плоскость y 1 (рис. 14).

-1

Рис. 13

Рис. 14

Рис. 15

е) Уравнение плоскости 2x 3y 2z 1 задано в отрезках, числа a 2 ,

b 3, c 2 в знаменателях дробей равны координатам точек пересечения плоскости с осями Ox, Oy, Oz. Отмечаем на осях координат эти точки и проводим через них плоскость (рис. 15).

Пример 15. Написать уравнения плоскости, проходящей через точку M0 x0 0, y0 2, z0 0 и перпендикулярную вектору N A 1, B 2,C 3 .

Решение. В данном случае удобно записать уравнение плоскости в виде (15)

A x x0 B y y0 С z z0 0 1 x 0 2 y 2 3 z 0 0

1 x 0 2 y 2 3 z 0 0 x 2y - 3z - 4 0 .

Пример 16. Написать уравнение плоскости, проходящей через три точки

M0 x0 1, y0 2, z0 0 , M1 x1 1, y1 0, z1 1 , M2 x2 0, y2 1, z2 3 .

Решение. В

ввиде (16)

xx0 x1 x0 x2 x0

x 1	y 2	z
x 1	y 2	z
0	2	1
1	1	3

данном случае удобно записать уравнение плоскости

y y0	z z0				x 1	y 2	z 0
y y0	z z0				x 1	y 2	z 0
y1 y0	z1 z0			0	1 1	0 2	1 0	0
y2 y0	z2 z0				0 1 1 2		3 0
раскладываем
по первой
строке		x	1 5 y 2 z 2				0 5x y 2z 7 0.
0		x	1 5 y 2 z 2				0 5x y 2z 7 0.

Проверка. Подставляя координаты точек M0, M1, M2

найденное

уравнение плоскости 5x y 2z 7 0 ,

получаем верные равенства, сле-

довательно, решение верно.

точки A 1, 4,0

Пример 17. Найти расстояние

от

до

плоскости

x 2 y 3z 1 0 .

Решение. d

Ax0 By0 Cz0 D

1 2 4 3 0 1

A2 B2 C2

12 2 2 3 2

Пример 18. Определить угол между плоскостями x 2 y 3z 1 0 и

x y z 0 .

Решение. Нормали данных плоскостей N1 1, 2, 3 , N2 1, 1,

1 опреде-

ляем из их уравнений, после чего находим косинус угла между плоскостями

cos	A1 A2 B1B2 C1C2						1 1 2 1 3 1		4
											.

	A12 B12 C12		2 B2	2 C2	2	12 2 2 3 2				42
		A2						12 12 12

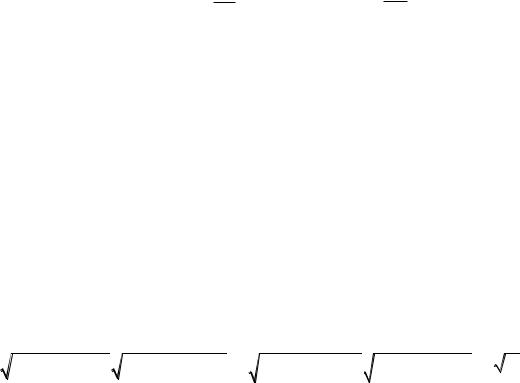
Пример 19. Даны координаты вершин тетраэдра ABCD (рис. 19) A 1,0,1 , B 1, 1,1 , C 0,2,1 , D 1,0,2 . Найти угол между его гранями

ABC и BCD .

Решение. Известны три точки A 1,0,1 , B 1, 1,1 , C 0,2,1 на плоскости ABC, найдем координаты векторов AB B A 0, 1,0 , AC C A 1, 2,0 и определим нормаль плоскости как векторное произведение

	i	j	k
				k 0,	0, 1 .
N ABC AB AC	0	1	0	k 0,	0, 1 .
	1	2	0

Аналогичным образом находим нормаль плоскости BCD

			C B 1,3,0 ,								D B 0,1,1 ;
		BC	C B 1,3,0 ,						BD		D B 0,1,1 ;
						i	j	k
						i	j	k
										3i j k 3, 1, 1 . .
	N BCD BC BD					1	3	0		3i j k 3, 1, 1 . .
						0	1	1
Зная нормали плоскостей ABC, BCD, определим косинус угла между ними
	A1 A2 B1B2 C1C2										0 3 0 1 1		1	1
cos	A1 A2 B1B2 C1C2													1		.

	A12 B12 C12 A2			2 B2	2 C2		2			02 02 1 2		32 12 1 2			11

Пример 20. Определить какие из заданных плоскостей 4x 2 y 1 0 ,2x 2 y 2z 1 0 , x 2 y 3z 1 0 и x y z 0 параллельны друг другу и какие перпендикулярны.

Решение. Нормали данных плоскостей N1(4, 2, 0), N2(–2, –2, –2), N3(1, –2, –3), N4(1, 1, 1) определяем из их уравнений и поверяем их на параллельность и перпендикулярность, используя соответствующие признаки.

а)

N1 4, 2, 0 ,

N2 2, 2, 2 не перпендикулярны, так как

N1 N2 4 2 2 2 12 0 ;

4, 2, 0 и

2, 2, 2 не параллельны, так как

;

б)

N1 4, 2, 0 N3 1, 2, 3 , так как N1 N3 4 1 2 2 0 ;

в)

N1 4, 2, 0

и N4 1, 1, 1 не перпендикулярны, так как

N1 N4 4 1 2 1 6 0 ;

4, 2,0 и

1, 1, 1 не параллельны, так как

;

г)

N2 2, 2, 2 , N3 1, 2, 3 не перпендикулярны, так как

N2 N3 2 1 2 2 2 3 8 0 ;

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1510 11 12 13 14 15 > Следующая >>>

Соседние файлы в предмете Линейная алгебра