7. АЛГЕБРА МНОГОЧЛЕНОВ

Определение 1. Многочленом (или, что то же самое, полиномом) п-й

называется функция вида

многочлен степени два, P0 z 4 - многочлен степени ноль.

Пример 1. Найти сумму, разность и произведение следующих двух

ведения многочленов равна пяти.

Определение 2. Отношение двух многочленов называется рациональной функцией (степень знаменателя не равна " " ) или рациональной дро-

Определение 3. Рациональная дробь называется правильной, если степень числителя строго меньше степени знаменателя. Например, рациональ-

ветственно, причем m n , n . Делением с остатком многочлена Pm z

на многочлен Qn z называется процесс отыскания таких двух новых многочленов q z и r z называемых соответственно «неполным частным» и «остатком», что выполняется равенство

77

причем степень остатка r z обязательно должна быть строго меньше степени делителя Q z , а степень неполного частного равна m n . Если в (2) r z 0 , то Pm z делится на Qn z без остатка. Легко доказать, что деление с остатком всегда осуществимо, а деление без остатка не всегда.

остаток равен нулю и деление выполнено без остатка;

в) для деления с остатком следующей рациональной дроби

2z2 z 1

2z2 5

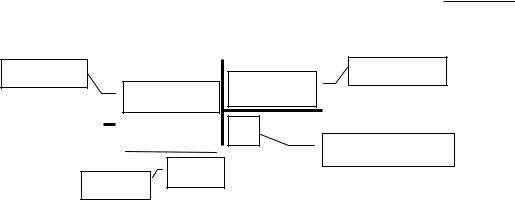
применим аналог деления «уголком» целых чисел (рис. 1).

Рис. 1

Слева от уголка запишем числитель дроби 2z2 z 1, в верхней правой части уголка знаменатель 2z2 5 , дальнейшие действия разбиваются на отдельные шаги, число которых меньше либо равно разности степеней числителя и знаменателя дроби плюс единица (в данном примере разность равна нулю, значит, число шагов равно единице).

Шаг 1. Делим старшую степень 2z2 числителя с соответствующим коэффициентом на старшую степень знаменателя 2z2 также с коэффициентом и записываем результат "1" в нижнюю правую часть уголка. Затем отнимаем знаменатель 2z2 5 , умноженный на полученную "1" от числителя 2z2 z 1, разность z 6 записываем под чертой. Выполненный шаг является последним, так как после него степень остатка z 6 строго меньше степени знаменателя 2z2 5 .

Ответ. Записываем результат деления с остатком в виде (2)

78

зультат 2z в нижнюю правую часть уголка. Затем отнимаем умноженный на 2z знаменатель z2 5 от числителя 2z3 2z2 , разность 2z3 10z записываем под чертой. Выполненный шаг не является последним, так как степень остатка 2z2 10z после первого шага равна степени знаменателя z2 5.

Шаг 2. Делим старшую степень 2z2 остатка 2z2 10z на старшую степень z2 знаменателя z2 5 и прибавляем полученное частное 2 в нижнюю правую часть уголка (к неполному частному). Затем отнимаем умноженный на 2 знаменатель z2 5 от остатка 2z2 10z после первого шага, полученную разность 10z 10 записываем под чертой. Выполненный шаг является последним, так как степень остатка 10z 10 после второго шага строго меньше степени знаменателя z2 5.

Ответ. Записываем результат деления с остатком в виде (2)

Определение 5. Корнем многочлена P(z) называется любое число z0

такое, что P(z0) = 0.

По теореме Безу многочлен P(z) делился на двучлен z z0 без остатка

тогда и только тогда, когда число z0 является корнем этого многочлена. Определение 6. Натуральное число k называется кратностью корня z0, ес-

Известно, что во-первых любой многочлен n-й степени имеет ровно n корней, среди которых могут быть вещественные и комплексные, во-вторых если комплексное число является корнем многочлена, то и сопряженное ему число также является корнем той же самой кратности, в-третьих если многочлен имеет k различных вещественных корней x1, x2, …, xk, кратности m1, m2, …, mk соответственно и s различных пар комплексно сопряженных корней, кратности которых равны r1, r2, …, rk, то этот многочлен можно записать в каноническом виде:

79

Известно, что произведение всех корней многочлена Pn z с0 zn c1zn 1

cn 1z cn равно cn , а сумма всех его корней равна c1 . Этот факт, может

быть полезен при нахождении корней многочлена.

P3 z . Поскольку P3 1 4 0 , P3 2 20 0 , P3 3 60 0 , то числа –1, 2, 3 не являются корнями P3 z . Так как многочлен третей степени P3 z име-

ет ровно три корня, то числа 1, 2, 3 и только они являются корнями P3 z , причем кратность каждого корня равна единице. Тогда по формуле (3) имеем

P3 z z 1 z 2 z 3 .

Так как дискриминант квадратного трехчлена z2 + 1 меньше нуля, то вещественных корней у него нет и потому его нельзя разложить на произведение линейных сомножителей.

Окончательно получаем каноническое представление исходного многочлена

z4 2z3 2z2 2z 3 z 1 z3 3z2 2z 6 z 1 z 3 z2 1 .

80

8. МОДЕЛЬ МЕЖОТРАСЛЕВОГО БАЛАНСА ЛЕОНТЬЕВА

Определение 1. Экономическая отрасль называется чистой, если она выпускает однородную продукцию, например энергетическая отрасль производит электроэнергию.

Определение 2. Система экономических отраслей называется замкнутой, если в процессе производства используются лишь продукты, производимые внутри системы.

Определение 3. Валовой выпуск j-й чистой отрасли за плановый период называется интенсивностью этой отрасли.

Определение 4. Если экономическая система состоит из n чистых от-

тором выпуска или просто выпуском системы.

Определение 5. Продукт, выпускаемый j -отраслью будем называть j - продуктом. Обозначим через ai, j количество i -продукта, потребляемого j -

составленная из этих коэффициентов, называется матрицей прямых затрат. Известно [1, 2], что вектор AX равен производственным затратам

на выпуск Х.

Определение 6. Разность C X AX валового выпуска X и производственных затрат AX на такой же валовой выпуск X в следующем производственном цикле называется конечным продуктом.

Определение 7. Система уравнений

вместе с экономической интерпретацией входящих в нее величин называет-

ся экономико-математической моделью Леонтьева межотраслевого ба-

ланса производства и распределения продукции или системой уравнений межотраслевого баланса. В матричной форме система (1) принимает вид

С системой (1) связаны два типа задач.

81

1)Найти значения конечного продукта C, когда известна матрица прямых затрат A и вектор выпуска X. Решение этой задачи, как следует из (2), тривиально.

2)Найти выпуск (валовой продукт) X, обеспечивающий заданный конечный продукт C, когда известна матрица прямых затрат A. Решение этой задачи дает формула

d1, j

трицей полных затрат. Столбец матрицы полных затрат равен вало-

dn, j

вому выпуску X, обеспечивающему производство одной единицы конечного продукта j -вида.

Пример 1. Замкнутая экономическая система состоит из трех чистых отраслей A, B,C . Межотраслевые поставки и валовые выпуски отраслей системы приведены в табл. 1.

1) Вычислить матрицу прямых затрат A.

2) Найти вектор производственных затрат на заданный выпуск.

3) Найти вектор конечного продукта при заданном выпуске.

4) Найти матрицу полных затрат.

5) Найти выпуск, необходимый для производства конечного продукта

ставок (здесь xi, j – объем продукта i, потребляемый отраслью j)

82

иначе, отнимая от валового выпуска каждой отрасли все межотраслевые поставки ее продукции:

Разница между найденными значениями объясняется тем, что коэффициенты прямых затрат были найдены приближенно с точностью до четвертого знака после запятой.

3) По формуле (2) найдем вектор конечного продукта C при заданном

600

выпуске X 400 с учетом того, что Y AX

400

83

Вычисляем определитель либо по правилу Сарюса, либо раскладывая его по любому ряду.

5) Найдем выпуск, необходимый для производства конечного продукта

18) Вычисление обратной матрицы смотри в главе 1, п. 1.5.

84