1.8. Приближенные формулы в схеме бернулли

Если число испытаний n велико, то применение формулы Бернулли приводит к громоздким вычислениям. В таких случаях пользуются приближенными формулами Пуассона или Муавра-Лапласа.

Если число испытаний n достаточно велико, а вероятность p достаточно мала ( <10), то вероятность можно приближенно вычислить по формуле:

, где a = np.

Обобщенная формула Пуассона имеет вид:

или

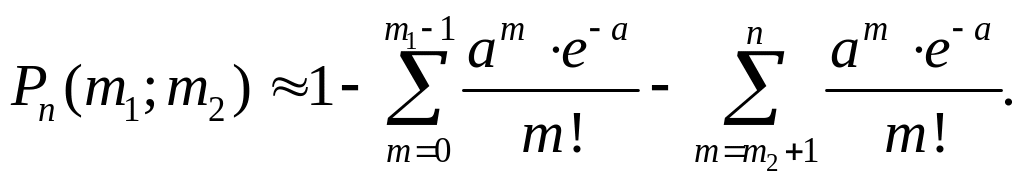
На практике обычно применяется та из двух приведенных формул, в которой меньше слагаемых. Если , то в последней формуле отсутствует первая сумма; если , то – вторая.

Пример решения задачи.

Задача №8. Садоводческий кооператив застраховал на один год свои дачные дома от пожара. Каждый из шестисот домовладельцев внес по 150 рублей. Вероятность пожара в одном доме в течение года равна 0,005, а страховая сумма, выплачиваемая пострадавшему, составляет 12000 рублей. Какова вероятность того, что страховая компания понесет убыток?

Решение. По условию задачи данный кооператив внес в страховую компанию

150 600 = 90 000 рублей. Т.к. выплата одному пострадавшему составляет 12 000 рублей, то полученных средств компании будет достаточно на 90 000 : 12 000 = 7,5 страховых случаев.

Значит, компания понесет убыток в случае не менее восьми пожаров.

Испытание: страхование дачного домика от пожара.

Событие А – возгорание дачного домика.

Имеем независимые испытания, n=600. В каждом испытании всего два возможных элементарных исхода или . В каждом испытании вероятности остаются неизменными.

Значит, схема Бернулли реализуется.

Требуется вычислить Т.к. число n велико, вычислим npq:

npq = 600 0,005 0,995 = 2,985. Т.к. npq < 10, и число слагаемых велико, воспользуемся второй формулой Пуассона.

где a = np = 600 0,005 = 3.

Произведем вычисления:

1- 0,04979 ( 1 + 3 + 4,5 + 3,375 + 2,025 + 1,0125 + 0,4339 ) 1 – 0,9882 = 0,0118.

Ответ: 0,012.

Если число испытаний n достаточно велико, и вероятности p и q не очень близки к нулю (npq 10), то вероятность можно приближенно вычислить по локальной формуле Муавра-Лапласа: