1.2. Элементы комбинаторики

Комбинаторика – это раздел математики, исследующий приемы нахождения числа возможных выборок при тех или иных условиях из строго определенного конечного множества.

Основные правила комбинаторики

Правило суммы. Если некоторый объект а можно выбрать из множества А m способами и после каждого такого выбора объект b из множества B можно выбрать n способами, то выбрать объект а или b можно m + n способами.

Правило произведения. Если некоторый объект а можно выбрать из множества А m способами и после каждого такого выбора объект b из множества B можно выбрать n способами, то пару объектов (а;b) можно выбрать m·n способами.

Размещения из n элементов по m – это такие выборки, которые имея по m элементов, выбранных из числа данных n элементов, отличаются одна от другой либо составом элементов, либо порядком их расположения.

Число размещений из m элементов по n:

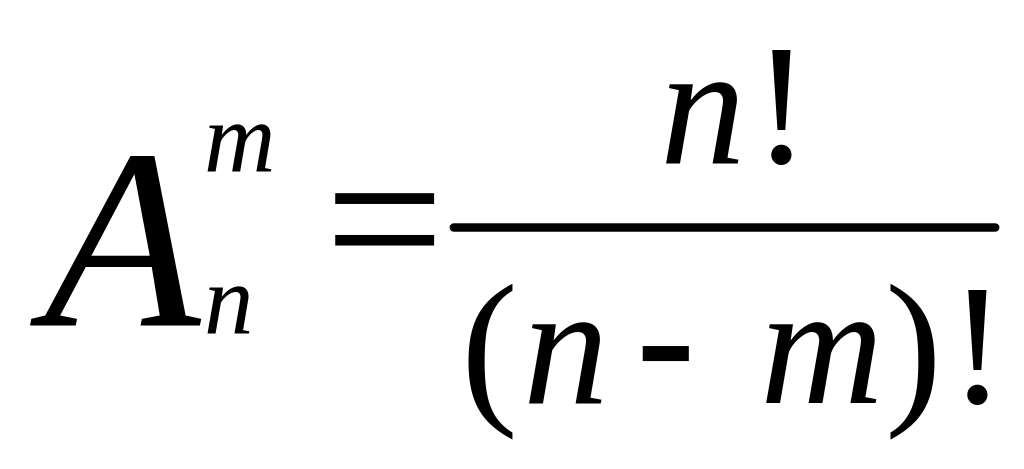
Перестановки из n элементов – это выборки, имеющие n элементов и отличающиеся одна от другой только порядком расположения элементов.

Число перестановок из n элементов: = n !

Сочетания из n элементов по m – это выборки, которые имея по m элементов, выбранных из числа данных n элементов, отличаются одна от другой хотя бы одним элементом.

Число сочетаний из n элементов по m: =

Выборки с повторениями – это выборки, содержащие одинаковые элементы.

Число размещений с повторениями: =

Число перестановок с повторениями:

( …, ) = ,

где - число одинаковых элементов i-го рода, причем

Число сочетаний с повторениями .

1.3. Алгоритм решения задачи на определение вероятности

1) Внимательно прочитать ( и возможно не один раз ) условие задачи, определить и записать, в чем заключается испытание.

2) Записать формулировку события, вероятность которого требуется вычислить.

3) Определить число m исходов, благоприятствующих в данном испытании рассматриваемому событию, используя при необходимости сведения из комбинаторики.

4) Определить общее число n равновозможных исходов данного испытания.

5) Вычислить вероятность по формуле

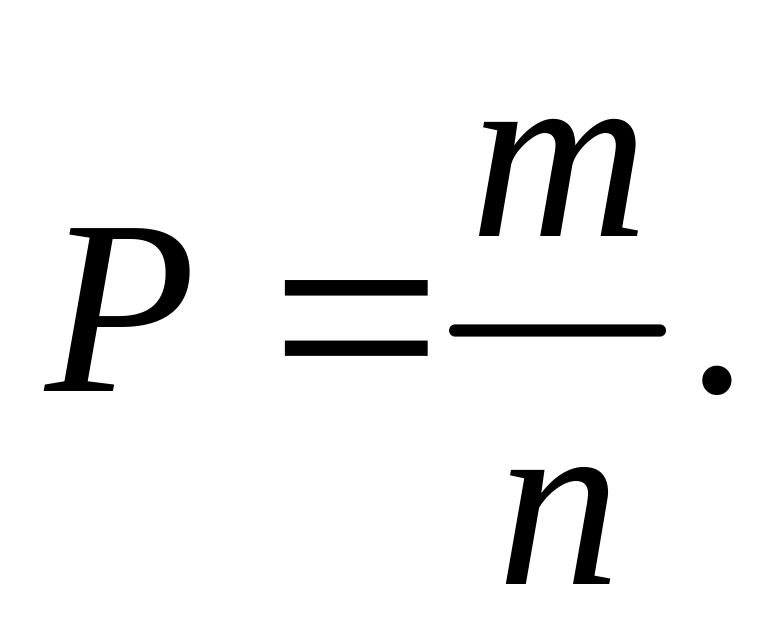
6) Записать ответ.

Примеры решения задач.

Задача №1. Жюри конкурса определило десять претендентов, одинаково достойных первой премии. Среди них оказалось пять научных сотрудников, два студента и трое рабочих. Найти вероятность того, что в результате жеребьевки премия будет выдана ученому или рабочему.

Решение. Испытание: выбор по жребию одного претендента из десяти

возможных.

Событие А – из десяти претендентов выбран ученый или рабочий.

Т.к. по условию задачи число научных сотрудников равно пяти и число рабочих равно трем, то по правилу суммы число благоприятствующих событию А исходов равно: m=5+3=8. Общее число всех возможных элементарных исходов по условию равно десяти: n=10. Согласно классическому определению вероятности:

Ответ: 0,8.

Задача №2. Группа туристов из 15 юношей и 5 девушек выбирает по жребию хозяйственную команду в составе четырех человек. Какова вероятность того, что в числе выбранных окажутся двое юношей и две девушки?

Решение. Испытание: выбор по жребию четырех человек из двадцати.

Событие А – в числе выбранных двое юношей и две девушки.

Составим схему выбора:

Всего юношей девушек

20 = 15 + 5

4 = 2 + 2

Имеем выборки без повторений, которые отличаются одна от другой только составом и не являются упорядоченными. Это сочетания. Значит, двух юношей из пятнадцати возможно выбрать способами, и двух девушек из пяти - способами. Тогда по правилу произведения событию А благоприятствует исходов испытания.

Аналогично подсчитаем общее число равновозможных исходов в данном испытании:

Вероятность события А вычислим по определению:

т.е.

Выразим каждое число сочетаний:

Подставим в выражение Р(А) и произведем вычисления:

Ответ: 0,22.