Федеральное агентство по образованию
Сочинский Государственный Университет Туризма и Курортного дела
Факультет информационных технологий и математики
Кафедра прикладной математики
Л.М.Вербина
Теория вероятностей и математическая статистика
Методические указания и контрольные задания по математике
для студентов специальности 270105
«Городское строительство и хозяйство»
Сочи, 2008 г.
Рекомендовано к печати кафедрой прикладной математики
факультета информационных технологий и математики
Сочинского государственного университета туризма и курортного дела
Рецензент: Е.Н. Пересыпкин, д.т.н., профессор
Л.М. Вербина. Теория вероятностей и математическая статистика: Методические указания и контрольные задания по математике для студентов специальности 270105 "Городское строительство и хозяйство"/ Авт.-сост. Вербина Л.М. – Сочи: СГУТиКД, 2008. – 80 с.
Указания содержат контрольную работу по теории вероятностей и математической статистике для студентов заочной формы обучения инженерных специальностей, справочный материал к заданиям, рекомендации к выполнению заданий, алгоритмы и детально разобранные примеры решения типовых задач, список рекомендуемой литературы и таблицы, необходимые для расчетов. Указания предназначены для организации самостоятельной работы студентов-заочников в четвертом семестре.
Содержание
Предисловие…………………………………………………………………………5
Раздел 1. Элементы теории вероятностей
Глава 1. Случайные события
1.1. Испытание, события, вероятность …….…………………………….………...6
1.2. Элементы комбинаторики….……………………………………...…………...7
1.3. Алгоритм решения задачи на определение вероятности ……………………8
1.4 Алгебра событий…….………………………………………………..………...11
1.5. Алгоритм решения задачи на алгебру событий…...…………………..……..11
1.6. Формула полной вероятности. Формула Байеса…..………………………...14
1.7. Схема испытаний Бернулли..…………………………………………………16
1.8. Приближенные формулы в схеме Бернулли………..………………………..19
1.9. Алгоритм решения задачи на схему Бернулли..……………………………..21
Глава 2. Случайные величины
2.1. Основные понятия……………………………………………………………..22
2.2. Числовые характеристики случайной величины…………………………….24
2.3. Нормальное распределение непрерывной случайной величины…………...29
Раздел 2. Элементы математической статистики
Глава 3. Выборочный метод и статистическое оценивание
3.1. Предмет и основные задачи математической статистики…………….…….31
3.2. Статистический ряд……………………………………………………………31
3.3. Статистические оценки параметров распределения………………………...34
3.4. Статистическая проверка статистических гипотез………………………….37
3.5. Алгоритм проверки гипотезы о нормальном распределении генеральной совокупности………………………………………………………………………..38
Глава 4. Элементы корреляционного и регрессионного анализа
4.1. Линейная корреляционная зависимость……………………………………...41
4.3. Проверка гипотезы о значимости выборочного коэффициента
корреляции …………………………………………………………………………44
Контрольная работа № 4………..…………………………………………………48
Учебно-методическое обеспечение дисциплины………………………………...74
Приложение 1 Таблица
значений функции Гаусса
……………...75
Приложение 2 Таблица
значений функции Лапласа
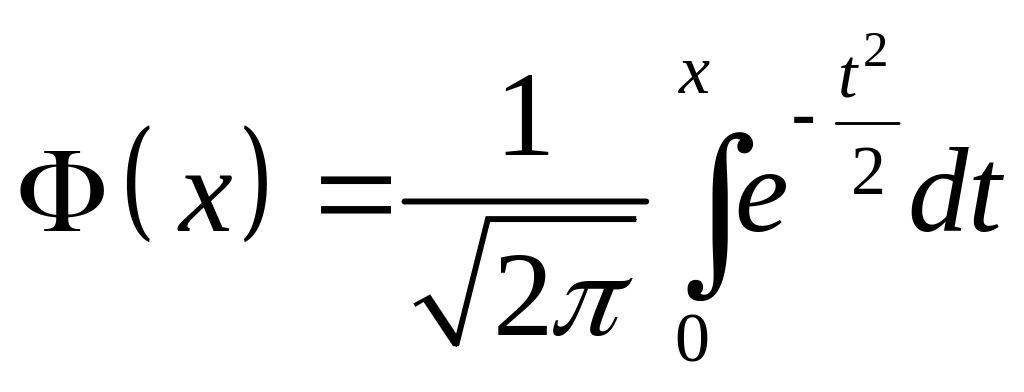………...76
Приложение 3 Таблица
значений коэффициентов Стьюдента
……..78
Приложение 4
Критические точки распределения
……………………..79
Приложение 5 Критические точки распределения Стьюдента………………….80