3.9.2. Несобственный интеграл от разрывной функции (2 рода)

Определение. Пусть функция f(x) определена и непрерывна на полуинтервале [а, b) , а при x=b либо не определена, либо имеет разрыв. Тогда предел 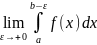называется несобственным интегралом от разрывной функции или несобственным интегралом 2 рода, то есть

Если этот предел существует и конечен, несобственный интеграл называется сходящимся, если же предел бесконечен или не существует - расходящимся.

Аналогично определяются несобственные интегралы с разрывом подынтегральной функции при

и во внутренней точке .

Этот интеграл сходится, если существуют и конечны оба предела.

Приведем примеры исследования несобственных интегралов на аходимооть при помощи определения.

Пример 18. Вычислить несобственный интеграл или доказать его расходимость.

Решение. Подынтегральная функция имеет разрыв при X = 5, поэтому по определению , то есть интеграл сходится и равен .

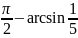Пример 18. Вычислить несобственный интеграл 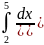или доказать его расходимость.

Решение. Подынтегральная функция не определена при х=3, поэтому то есть интеграл расходится.

Сформулируем признаки сходимости несобственных интегралов от разрывной функции.

Теорема 7. Пусть на полуинтервале выполняются неравенства 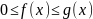, а в точке x=b функции f(x) и g(x) либо имеют разрыв, либо не определены. Тогда:

1. Если интеграл сходится, то интеграл также сходится.

2. Если интеграл расходится, то интеграл также расходится.

Теорема 8. Пусть на полуинтервале выполнены следующие условия: 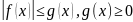, а функции f(x) и g(x) либо имеют разрыв, либо не определены при x=b. Тогда из сходимости интеграла следует сходимость интеграла .

Определение. Пусть функция f(х) определена на , а в точке b либо не определена, либо имеет разрыв. Тогда интеграл называется абсолютно сходящимся, если 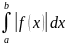сходится, и условно сходящимся, если расходится, а сходится.

Теорема 9. Пусть на полуинтервале выполняются следующие условия: функции f(x) и g(x) неотрицательны, и .

Тогда:

1. Если и интеграл сходится, то интеграл также сходится.

2. Если и интеграл расходится, то интеграл также расходится.

В частности, есл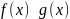и при 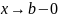(то есть ), то интегралы и сходятся или расходятся одновременно.

Замечание. В качестве интеграла сравнения часто берут интеграл 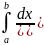, который сходится при и расходится при .

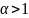Аналогичные теоремы можно сформулировать, когда функция имеет разрыв или не определена в точке х=а.

Пример 20. Исследовать на сходимость интеграл .

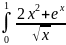Решение. Подынтегральная функция имеет разрыв при х=0. Выберем в качестве функции сравнения функцию . Имеем , но интеграл сходится (см. замечание к теореме 9), поэтому исходный интеграл также сходится.

В заключение заметим, что если исследуемый интеграл содержит одновременно особенности I и П рода, то для исследования его на сходимость он представляется в виде суммы интегралов, каждый из которых имеет особенность только одного рода, например:

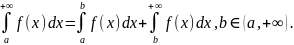
(предполагается, что подынтегральная функция непрерывна на интервале и имеет разрыв или не определена при x=a .Походный интеграл будет сходящимся, воли сходятся оба интеграла в правой части равенства и расходящимся, если расходитоя хотя бы один из них.