Билеті №1 Сандардың арасындағы арақашықтық

а) сандардың арасындағы арақашықтық. X=R-барлық нақты сандар жиыны делік. 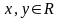арасындағы арақашықтықты осы сандардың айырымының модулымен анықтайды, яғни

(1.1)

Геометриялық тұрғыда бұл арақашықтық х және у нүктелерін қосатын сандық түзу кесіндісінің ұзындығына тең болады.

Векторлар арасындағы арақашықтық

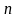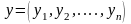
векторлар арасындағы арақашықтық. -барлық -өлшемді сандық векторлар жиыны делік. , -екі вектор болсын. Олардың арасындағы арақашықтық әртүрлі әдіспен анықталады:

1. ; (1.2a)

2. ; (1.2б)

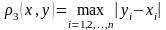3. . (1.2в)

Мысалы: векторлар және 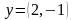берілсін. , және арақашықтықтарды табалық.

;

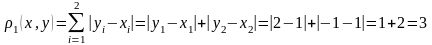Векторлардың сәйкес координаталарының арасындағы арақашықтық векторлардың арасындағы арақашықтықтан аспайтынына оңай көз жеткізуге болады, яғни

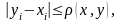
Билеті №2 Функциялардың арасындағы арақашықтық

функциялардың арасындағы арақашықтық. және g - және D_g сәйкес анықталу облысында анықталған нақты айнымалылардың нақты функциялары делік . және g мәндері нақты сан болады. Сондықтан мәндерінің арасындағы арақашықтық келесі формуламен анықтауға болады:

(1.4)

Енді және g бір айнымалының функциялары болсын делік. Егер және g кесіндісінде анықталған және үзіліссіз болса, онда пен g арасындағы арақашықтық

(1.5)

формуласымен анықтауға болады. Кейде арақашықтықты

(1.6)

формуласымен де анықтайды.

Мысал: 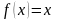және 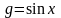функцияларының бірі-бірінен аралықта қандай арақашықтықта болатынын белгіміз келді делік. (1.5) формула бойынша

.

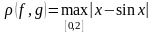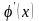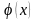
кесіндісіне функциясын ендірелік. Сонда  кесіндісінде 0. Ең үлкен мәнін функция нүктелерінде қабылдайды.

.

Абсолютті қателік

Жуықталған санының шекті абсолют қателігі деп осы санының абсолют қателігінен аз болмайтын санды айтады, яғни

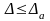(2.3)

Ол сан бірмәнді (не однозначно) анықталмайды: оны өсіруге болады.

Сонда (2.3)-ден алатынымыз:

(2.4)

Демек

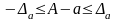
, (2.5)

Яғни 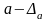кемімен алған А санының жуықталған мәні, ал 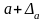– А санының артығымен алынған жуық мәні. (2.5) формуланы қысқаша былай жазуға болады:

(2.6)

Практикада шаманың дәлдігін түсіну кезінде шекті абсолют қателігін пайдаланады. Мысалы, егер екі пунктің S=900 м тен арақашықтық 0,5 м дәлдікпен алынса, онда S шаманың дәл мәні

899,5 м < S < 900,5 м

шекаралықты алынатын болады.

Әдетте абсолют қателік (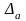 ) екі-үш маңызды (значащие) таңбалы санмен жазады, ал маңызды таңбаларды санау кезінде сол жақтағы нольдер саналмайтынын естен шығармау керек. Мысалы: 0,004060 санында 4 маңызды таңба бар.

Мысалы: ! қандайда бір есептеу машинасына тек 3 маңызды таңбалы сандарды ғана енгізу мүмкін болсын. 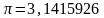онда 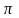санын қандай дәлдікпен енгізуге болады. Шешімі: деп алуға болады.