
1- 5_Финансовый менеджмент (Вариант 5, автор методички Ф.А.Красина)
.rtf
Федеральное агенство по образованию
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра экономики
Контрольная работа
по дисциплине «Финансовый менеджмент»
2008
вариант 5
Задача 1. Банк выдал ссуду на 35 дней в размере 80 тыс. руб. под простую процентную ставку 30% годовых. Рассчитать доход банка, если при начислении простых процентов считается, что в году: а) 360 дней; б) 365 дней.
Решение:
Пускай
P
= 80000 руб. – сумма, полученная заемщиком,
r
= 0.30 – простая процентная ставка, t
= 35 – продолжительность операции в днях,
T
– количество дней в году а) 360 дней; б)
365 дней. Определим доход банка
D=F–P,
по следующей формуле
 :
:
а)
 руб.
руб.
б)
 руб.
руб.
Ответ: Доход банка а) 2333 рубля, б) 2301 рубль.
Задача 2. Векселедержатель 20 февраля предъявил для учета вексель со сроком погашения 31 марта того же года. Банк учел вексель по простой учетной ставке 30 % годовых и выплатил клиенту 19 тыс. руб. Какой величины комиссионные удержаны банком в свою пользу, если год високосный?
Решение:
По
данной формуле
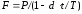 определим
сумму векселя, где P
= 19000 рублей, d
= 0.30, t
= 40 дней (с 20 февраля по 31 марта), год
високосный, следовательно, Т = 366.
определим
сумму векселя, где P
= 19000 рублей, d
= 0.30, t
= 40 дней (с 20 февраля по 31 марта), год
високосный, следовательно, Т = 366.
 рублей.
рублей.
Найдем комиссионные банка: F – P = 19640 – 19000 = 640 рублей.
Ответ: банком удержаны комиссионные в размере 640 рублей.
Задача 3. За какой срок исходная сумма в 15 тыс. руб. возрастет до 50 тыс. руб., если сложные проценты по процентной ставке 28 % годовых начисляются: а) ежегодно; б) ежеквартально; в) ежемесячно?
Решение: Пусть F = 50000 руб., P = 15000 руб., r = 0.28, а) m = 1, б) m = 4, в) m = 12.
Срок, за который первоначальная сумма возрастет до требуемой, определим по формуле:
а)
 - при начислении процентов ежегодно;
- при начислении процентов ежегодно;
б)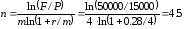 - при начислении процентов ежеквартально;
- при начислении процентов ежеквартально;
в) - при начислении процентов ежемесячно.
- при начислении процентов ежемесячно.
Ответ: исходная сумма в 15 тыс. руб. возрастет до 50 тыс. руб. при начислении процентов ежегодно за 4,9 года, при начислении процентов ежеквартально 4,5 года, при начислении процентов ежемесячно за 4,4 года.
Задача 4. Какую сумму необходимо поместить в банк под сложную процентную ставку 30 % годовых, чтобы накопить 400 тыс. руб.: а) за 6 лет при ежегодном начислении процентов; б) за 4 года при ежемесячном начислении процентов?
Решение:
Пусть
F
= 400000 руб.; r
= 0.30; а) количество начислений в год m
= 1, продолжительность периода в годах
n
= 6; б) m
= 12, n
= 4; P
– неизвестна. Для того чтобы найти
первоначальную сумму воспользуемся
следующей формулой
 .
.
а)
 рублей;
рублей;
б)
 рублей.
рублей.
Ответ: чтобы накопить 400 тыс. руб. необходимо поместить в банк а) на 6 лет при ежегодном начислении процентов 82,87 тыс. руб.; б) на 4 года при ежемесячном начислении процентов 122,3 тыс. руб.
Задача 5. Вы имеете вексель на сумму 150 тыс. руб. и хотели бы при учете по сложной учетной ставке за 2 года до срока погашения получить 3/5 этой суммы. Какая должна быть годовая учетная ставка при дисконтировании поквартально?
Решение:
годовую
учетную ставку при дисконтировании
поквартально найдем по формуле
 ,
при P
= 3/5F=3/5∙150000=90000
руб., n
= 2, m
= 4. В итоге получим
,
при P
= 3/5F=3/5∙150000=90000
руб., n
= 2, m
= 4. В итоге получим

Ответ: годовая учетная ставка = 24.7%.
Задача 6. Рассчитайте эффективную годовую процентную ставку, если номинальная ставка равна 10 % годовых и проценты начисляются: а) ежегодно; б) ежеквартально; в) ежемесячно.
Решение:
Эффективную
годовую процентную ставку рассчитаем
по следующей формуле:
 ,
где re
–
эффективная ставка, r
= 0,10 – простая процентная ставка, а) m
= 1 – количество начислений в году, б) m
= 4, в) m
= 12.
,
где re
–
эффективная ставка, r
= 0,10 – простая процентная ставка, а) m
= 1 – количество начислений в году, б) m
= 4, в) m
= 12.
а)
При ежегодном начислении процентов -
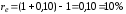
б)
При ежеквартальном начислении процентов
-

в)
При ежегодном начислении процентов -

Ответ: Эффективная годовая процентная ставка равна при начислении процентов а) ежегодно – 10 %; б) ежеквартально – 10,38 %; в) ежемесячно – 10,47%.
Задача 7. На вклад в течение 18 месяцев начисляются проценты: а) по схеме сложных процентов; б) по смешанной схеме. Какова должна быть годовая процентная ставка, при которой происходит реальное наращение капитала, если каждый квартал цены увеличиваются на 12 %.
Решение:
Определим
индекс инфляции I.
Так как каждый квартал происходит
увеличение цен на 12 %, то индекс инфляции
будет равен (1+0,12) 1,12. Квартал составляет
0,25 года, в нашей задаче 6 кварталов или
1,5 года, следовательно, индекс инфляции
за 18 месяцев составит
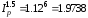
Далее
найдем годовую процентную ставку при
начислении сложных процентов по формуле:
(1+r)1,5
=
1,9738, где через r
обозначена искомая годовая процентная
ставка.
 .
Следовательно, ставка должна превышать
57,35 % годовых.
.
Следовательно, ставка должна превышать
57,35 % годовых.
При
начислении процентов по смешанной схеме
приравняем индекс инфляции за 18 месяцев
к множителю наращения и получим квадратное
уравнение относительно искомой годовой
процентной ставки – r
 ,
откуда r
= -3,562 и r
= 0,562. Таким образом, при использовании
смешанной схемы ставка должна превышать
56,20 % годовых, первый корень отпадает.
,
откуда r
= -3,562 и r
= 0,562. Таким образом, при использовании
смешанной схемы ставка должна превышать
56,20 % годовых, первый корень отпадает.
Начисление процентов по смешанной схеме более эффективно, чем в первом случае.
Ответ: а) r > 57.35%, б) r > 56.20 %.
Задача 8. Клиент в конце каждого года вкладывает 30 тыс. рублей в банк, начисляющий сложные проценты по ставке 10 % годовых. Определите сумму, которая будет на счете клиента через: а) 3 года; б) 8 лет; в) 15 лет. Как изменятся найденные величины, если деньги вкладываются в начале года?
Решение:
Для
определения суммы, которая будет на
счете клиента, воспользуемся формулой
 ,
,
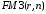 вычислим непосредственно по формуле
вычислим непосредственно по формуле
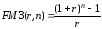 .
Пусть А = 30, r
= 10% = 0,10, в зависимости от варианта
количество периодов равно а) n
= 3; б) n
= 8; в) n
=15.
.
Пусть А = 30, r
= 10% = 0,10, в зависимости от варианта
количество периодов равно а) n
= 3; б) n
= 8; в) n
=15.
а)
 ;
;
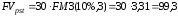 тыс.
руб.
тыс.
руб.
б)
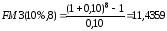
 тыс.
руб.
тыс.
руб.
в)

 тыс.
руб.
тыс.
руб.
Если платежи будут поступать в начале года суммы изменяться следующим образом:
а)
 ;
;
 тыс.
руб.
тыс.
руб.
б)

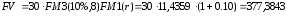 тыс.
руб.
тыс.
руб.
в)

 тыс.
руб.
тыс.
руб.
Ответ: если вклад вносить в начале года сумма увеличивается.
Задача 9. Клиент хочет накопить 800 тыс. руб., осуществляя в конце каждого года равные вклады в банк под сложную процентную ставку 16 % годовых. Какой величины должен быть вклад, чтобы накопить требуемую сумму: а) за 5 лет; б) 10 лет.
Решение:
Для
того чтобы определить
величину
вклада воспользуемся формулой
 .
Из этой формулы найдем А:
.
Из этой формулы найдем А:
 .
.
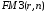 вычислим непосредственно по формуле
вычислим непосредственно по формуле
 .
.
1)
FV
= 800, r
= 16 % = 0,16, n
= 5.
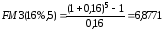 ,
,
 тыс.
руб.
тыс.
руб.
2)
FV
= 800, r
= 16 % = 0,16, n
= 10.
 ,
,
 тыс.
руб.
тыс.
руб.
Ответ: чтобы накопить требуемую сумму клиент должен вкладывать в конце каждого года а) за 5 лет 116,328 тыс. руб., б) за 10 – 37,521 тыс. руб.
Задача 10. Какую сумму необходимо поместить в банк под процентную ставку 20 % годовых, чтобы в течение 9 лет иметь возможность ежегодно получать по 120 тыс. руб., снимая деньги равными долями каждые 2 месяца и в конце девятого года исчерпать счет полностью, если банком начисляются сложные проценты: а) ежегодно; б) ежеквартально; в) ежемесячно?
Решение: Определим приведенную стоимость аннуитета постнумерандо при
А = 20 тыс. руб., так как деньги снимаются равными долями каждые 2 месяца, т.е. 6 раз в год 12 / 2 = 6; А = 120 / 6 = 20 тыс. руб.; n = 9∙6 = 54; r = 20 % / 6 = 0,0333; m = 1.
Воспользуемся следующей формулой:
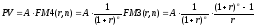 .
.
 тыс.руб.
тыс.руб.
б) А = 120 / 6 = 20 тыс. руб.; n = 9∙6 = 54; r = 20 % / 6 = 0,0333; m = 4; p = 1.
В
данном случае воспользуемся формулой

 ;
;
 ;
;


 тыс.руб.
тыс.руб.
в) А = 120 / 6 = 20 тыс. руб.; n = 9∙6 = 54; r = 20 % / 6 = 0,0333; m = 12; p = 1.
Как
и в предыдущем случае воспользуемся
формулой
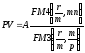 .
.
 ;
;
 ;
;


 тыс.руб.
тыс.руб.
Ответ: необходимо поместить в банк под процентную ставку, если сложные проценты начисляются: а) ежегодно – 497,87 тыс. руб.; б) ежеквартально – 493,906 тыс. руб.; в) ежемесячно – 492,977 тыс. руб.
Задача 11. Фирма намеревается выпускать некоторую продукцию в течение 4 лет, получая ежегодно выручку в размере 50 млн. руб. Предполагается, что продукция в течение года будет продаваться равномерно. Оцените ожидаемый доход фирмы, если применяется непрерывная ставка 22 % за год.
Решение:
Для
определения дохода фирмы воспользуемся
следующими формулами:

 ,
поскольку продажа продукции будет
происходить равномерно и денежные
поступления происходят непрерывно.
Пусть
,
поскольку продажа продукции будет
происходить равномерно и денежные
поступления происходят непрерывно.
Пусть
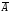 =50
млн. руб., n
= 4,
σ = 0,22, следовательно:
=50
млн. руб., n
= 4,
σ = 0,22, следовательно:
 млн.
руб. – будущая стоимость данного
денежного потока – непрерывного
аннуитета.
млн.
руб. – будущая стоимость данного
денежного потока – непрерывного
аннуитета.
 млн.
руб. – приведенная стоимость данного
денежного потока - непрерывного аннуитета.
млн.
руб. – приведенная стоимость данного
денежного потока - непрерывного аннуитета.
Ответ: будущая стоимость непрерывного аннуитета составляет 320,659 млн. руб., приведенная стоимость – 133,004 млн.руб.
Задача 12. За 5 лет необходимо накопить 400 тыс. руб. Какой величины должен быть первый вклад, если предполагается каждый год увеличивать величину денежного поступления на 15 % и процентная ставка равна 24 % годовых. Денежные поступления и начисление процентов осуществляются в конце года.
Решение:
Платежи
увеличиваются на 15 % либо в 1,15 раза. Для
определения первого платежа воспользуемся
следующей формулой:
 ,
где очевидно, что FV
= 400 тыс. руб., q
= 1,15, r
= 0,24, n
= 5.
,
где очевидно, что FV
= 400 тыс. руб., q
= 1,15, r
= 0,24, n
= 5.
Из
формулы
 выразим А:
выразим А:
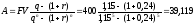 тыс.
руб.
тыс.
руб.
Ответ: первый вклад будет равен 39,119 тыс. руб.
Задача 13. Условно-постоянные расходы компании равны 12 млн. руб., отпускная цена единицы продукции – 16 тыс. руб., переменные расходы на единицу продукции -10. Рассчитайте:
-
критический объем продаж в натуральных единицах;
-
объем продаж, необходимый для достижения прибыли в 3 млн. руб.
Как изменятся значения этих показателей, если:
-
условно-постоянные расходы увеличатся на 15 %;
-
отпускная цена взрастет на 2 тыс. руб.;
-
переменные расходы возрастут на 10 %;
-
изменятся в заданной пропорции все три фактора?
Решение: Для решения данной задачи и проведения аналитического расчета введем обозначения:
Q – объем продаж в натуральных единицах,
P – цена реализации единицы продукции,
V – переменные расходы на единицу продукции,
FC – условно- постоянные расходы,
GI – прибыль до вычета процентов и налогов,
Qc – точка безубыточности.
В нашем примере FC = 12 млн. руб., P = 16 тыс. руб., V = 10 тыс. руб., GI = 3 млн. руб.
Расчет
будем производить, используя, следующую
базовую формулу:
 .
.
Критический
объем продаж в натуральных единицах
определим по формуле
 ,
так как данный объем продаж соответствует
безубыточности
,
так как данный объем продаж соответствует
безубыточности
 .
Итак, критический объем продаж
.
Итак, критический объем продаж
 ед.
Экономический смысл критического объема
продаж
заключается
в том, что при данном объеме прибыль
предприятия равна 0. Далее
определим объем
продаж необходимый для достижения
прибыли в 3 млн. руб. Воспользуемся
формулой
ед.
Экономический смысл критического объема
продаж
заключается
в том, что при данном объеме прибыль
предприятия равна 0. Далее
определим объем
продаж необходимый для достижения
прибыли в 3 млн. руб. Воспользуемся
формулой
 ед.
ед.
Далее проследим изменения значений полученных показателей:
-
условно-постоянные расходы увеличатся на 15 %;
FC = 13,8 млн. руб., P = 16 тыс. руб., V = 10 тыс. руб., GI = 3 млн. руб.
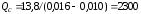 ед.
ед.
 ед.
ед.
Вывод: при увеличении на 15 % условно-постоянных расходов объем продаж увеличивается также на 15 %, а для достижения прибыли в 3 млн. руб. – на 12% .
-
отпускная цена возрастет на 2 тыс. руб.;
FC = 12 млн. руб., P = 18 тыс. руб., V = 10 тыс. руб., GI = 3 млн. руб.
 ед.
ед.
 ед.
ед.
Вывод: при увеличении на 2 тыс. руб. отпускной цены объем продаж в первом и во втором случае уменьшается 25%.
-
переменные расходы возрастут на 10 %;
FC = 12 млн. руб., P = 16 тыс. руб., V = 11 тыс. руб., GI = 3 млн. руб.
 ед.
ед.
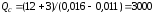 ед.
ед.
Вывод: при увеличении на 10 % переменных расходов увеличивается объем продаж на 20%.
-
изменятся в заданной пропорции все три фактора:
FC = 13,8 млн. руб., P = 18 тыс. руб., V = 11 тыс. руб., GI = 3 млн. руб.
 ед.
ед.
 ед.
ед.
Вывод: при изменении в заданной пропорции всех трех факторов объем продаж уменьшился на 1,43%, а для достижения прибыли в 3 млн. руб. – на 4% .
Ответ: критический объем продаж – 2000 ед., объем продаж для получения прибыли в 3 млн. руб. – 2500 ед.
Задача 14. Компания Х имела на 1 июня остаток денежных средств на расчетном счете в сумме 10000 руб. Компания производит продукцию со следующими удельными показателями:
- затраты сырья – 20 руб.;
- оплата труда – 10 руб.;
- прямые накладные расходы – 10 руб.
Известно, что объемы производства и продаж в натуральных единицах составили:
|
|
Июнь |
Июль |
Август |
Сентябрь |
Октябрь |
Ноябрь |
Декабрь |
|
Производство |
100 |
150 |
200 |
250 |
300 |
350 |
400 |
|
Продажа |
75 |
100 |
150 |
200 |
300 |
350 |
400 |
Требуется: составить прогноз движения денежных средств до конца 2001г., если имеется следующая информация:
-
цена реализации – 80 руб.;
-
все прямые расходы оплачиваются в том же месяце, когда они имели место;
-
продажа продукции осуществляется в кредит, период кредита – 1 месяц;
-
в июле компания приобрела новый станок за 20000 руб., оплата за станок – в октябре;
-
постоянные накладные расходы оплачиваются ежемесячно в сумме 1900 руб.
Решение:
|
Показатели |
Июнь |
Июль |
Август |
Сентябрь |
Октябрь |
Ноябрь |
Декабрь |
|
Денежные средства на 01.06.2001 |
10000 |
4100 |
2200 |
300 |
400 |
-17500 |
-9400 |
|
Поступления денежных средств |
|
|
|
|
|
|
|
|
Реализация продукции в кредит |
|
6000 |
8000 |
12000 |
16000 |
24000 |
28000 |
|
Итого поступлений |
0 |
6000 |
8000 |
12000 |
16000 |
24000 |
28000 |
|
Выбытие денежных средств |
|
|
|
|
|
|
|
|
Затраты на производство продукции |
4000 |
6000 |
8000 |
10000 |
12000 |
14000 |
16000 |
|
Постоянные накладные расходы |
1900 |
1900 |
1900 |
1900 |
1900 |
1900 |
1900 |
|
Приобретение оборудования |
|
|
|
|
20000 |
|
|
|
Итого выбытия |
5900 |
7900 |
9900 |
11900 |
33900 |
15900 |
17900 |
|
Денежные средства на конец месяца |
4100 |
2200 |
300 |
400 |
-17500 |
-9400 |
700 |
Ответ: На конец года остаток денежных средств предприятия составляет 700 рублей.
Задача 15. Эксперты компании Х составили сводные данные о стоимости источников в случае финансирования новых проектов (%):
|
Диапазон величины источника, тыс. руб. |
Заемный капитал |
Привилегированные акции |
Обыкновенные акции |
|
0-250 |
7 |
15 |
20 |
|
250-500 |
7 |
15 |
22 |
|
500-750 |
8 |
17 |
23 |
|
750-1000 |
9 |
18 |
24 |
|
Свыше 1000 |
12 |
18 |
26 |
Целевая структура капитала компании составляет:
- привилегированные акции – 15 %;
- обыкновенный акционерный капитал – 50 %
- заемный капитал – 35 %.
Требуется: рассчитать значение WACC для каждого интервала источника финансирования.
Решение:
|
Диапазон величины источника, тыс. руб. |
Заемный капитал |
Привилегированные акции |
Обыкновенные акции |
WACC |
|
0-250 |
7 |
15 |
20 |
14,7% |
|
250-500 |
7 |
15 |
22 |
15,7% |
|
500-750 |
8 |
17 |
23 |
16,85% |
|
750-1000 |
9 |
18 |
24 |
17,85% |
|
Свыше 1000 |
12 |
18 |
26 |
19,9% |
|
Удельный вес источника средств в общей их сумме, % |
35% |
15% |
50% |
|
WACC – это средняя взвешенная стоимость капитала, которая рассчитывается по формуле WACC = ∑ Ki ∙ Di, где Ki – стоимость источника средств, Di – удельный вес источника средств в общей их сумме.
WACC = 0,35 ∙ 7 + 0,15 ∙ 15 + 0,5 ∙ 20 = 14,7%
WACC = 0,35 ∙ 7 + 0,15 ∙ 15 + 0,5 ∙ 22 = 15,7%
WACC = 0,35 ∙ 8 + 0,15 ∙ 17 + 0,5 ∙ 23 = 16,85%
WACC = 0,35 ∙ 9 + 0,15 ∙ 18 + 0,5 ∙ 24 = 17,85%
WACC = 0,35 ∙12 + 0,15 ∙ 18 + 0,5 ∙ 26 = 19,9%
Ответ: значения WACC для каждого интервала источника финансирования указаны в таблице.
