Лекция 14.05.2020 г. (2 курс)

Строение одноэлектронных атомов

§1. Основное состояние

В этой лекции мы исследуем строение атома или иона с одним электроном, иначе говоря, изучим движение электрона в кулоновском поле ядра (рис.10). Потенциальная энергия зависит только от r:

, (47)

где .

Волновая же функция в общем случае зависит от трех пространственных координат, и для решения задачи нужно использовать трехмерное уравнение Шредингера. Однако, в состоянии с наименьшей энергией (в основном состоянии), как мы покажем ниже, -функция является сферически-симметричной, т.е. зависит только от r. В этом случае оператор Лапласа , и уравнение (24) принимает вид:

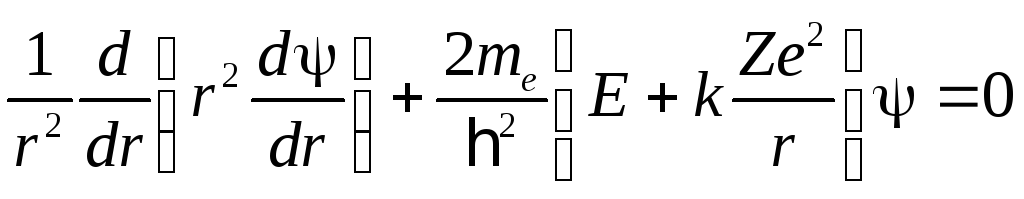(48)

а граничным условием будет:

. (49)

Решение уравнения (48) будем искать в виде:

(50)

Подставляя выражение (50) в уравнение (48) и произведя необходимые операции, приходим к системе двух уравнени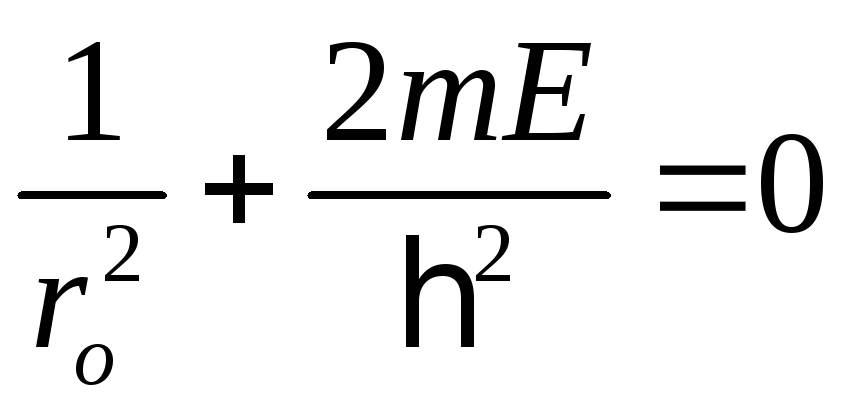й

и 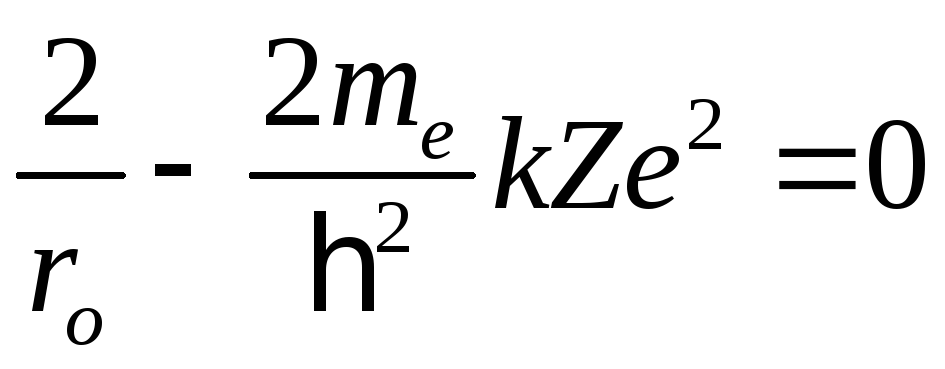, (51)

позволяющих определить r_o и собственное значение энергии Е:

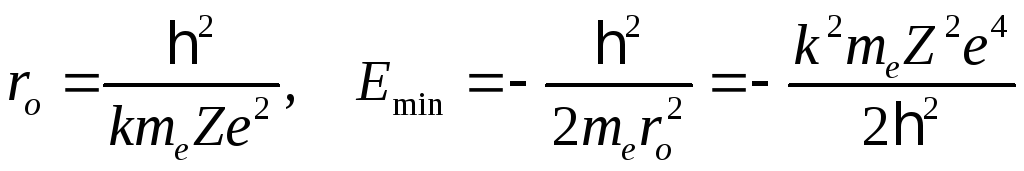(52)

По этому поводу следует сделать несколько замечаний. Во-первых, уравнения (51) вытекают из требования обращения в нуль коэффициентов при одинаковых степенях переменной r, ибо подстановка решения должна обращать его в тождество. Во-вторых, под m_e подразумевается не просто масса электрона m_eo, а так называемая приведенная масса электрона, равная m_eom_я/(m_eo + m_z), т.к. на самом деле электрон и ядро движутся около общего центра масс. (Правда отличие m_e от m_eo незначительно). В-третьих, E_min получается отрицательной (как и все остальные собственные значения), т.к. мы вычисляем фактически не полную энергию электрона с учетом энергии покоя, а только энергию связи электрона с ядром, которая не бесконечности обращается в нуль.

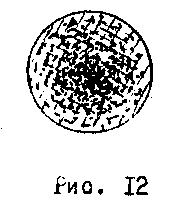
Для водорода (Z = 1) r_o = 0,53 , Е_min = – 13,5 эВ. На рис.11 показано распределение ||² и d/dr по радиусу. Как следует из формулы (50),

(53)

а

вероятность обнаружить электрон в элементе объема dV, находящемся на расстоянии r от ядра

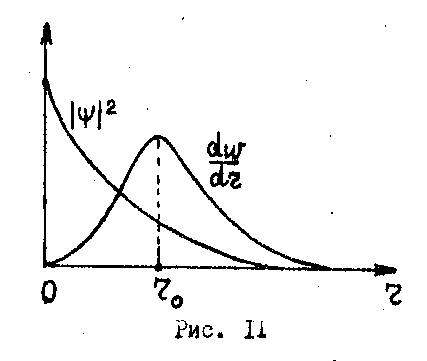
(54)

Нас не интересует направление, а только расстояние – поэтому объем dV равен объему шарового слоя толщиной dr, т.е. действительно, 4r²dr.

Из формулы (54) следует, что вероятность обнаружить электрон на расстоянии r от заряда, определяется функцией

(55)

Эта функция, как легко убедиться, имеет максимум при r = r_o.

Распределение же самой плотности вероятности ||² или, что безразлично, e||² называется электронным облаком и изображается обычно не в виде графика (как на рис.11), а в виде контурных диаграмм или рисунков, напоминающих обычные плоские фотографии объемного тела. В основном состоянии электронное облако имеет вид шарика, плотность которого резко убывает к краям (рис.12). Постоянная А определяется из условия нормировки

§2. Возбужденные состояния. Система трех квантовых чисел

Как уже упоминалось, в общем случае -функция зависит от трех координат (например, сферических).

Вследствие линейности уравнения Шредингера ее можно представить в виде произведения трех функций, каждая из которых зависит только от одной («своей») координаты. Каждая из этих функций характеризуется своим квантовым числом, поэтому полная -функция зависит уже не от одного квантового числа (как в одномерном случае), а сразу от трех квантовых чисел:

.

Эти три квантовых числа не только определяют собственные функции, но имеют другой, не менее важный, физический смысл. Познакомимся с ним поближе.

Главное квантовое число n определяет радиальную часть -функции и энергию стационарного состояния атома:

(56)

где Е₁ тождественно с Е_min из §10, а n принимает значения

n = 1, 2, 3,  (57)

Азимутальное квантовое число l определяет азимутальную часть -функции и среднее значение орбитального момента импульса электрона (или механического момента)

(58)

где l принимает значения

l =0, 1, 2,  , n – 1 (59)

Магнитное квантовое число m определяет полярную часть -функции и проекцию орбитального момента импульса на физически-выделенное направление z:

, (60)

где

m =  l,  (l – 1), , 1, 0, (61)

т.е. всего m принимает 2l + 1 различных значений. Под физически-выделенным направлением подразумевается направление любого физического поля (обычно магнитного, откуда и название «магнитное» квантовое число).

Из формул квантования (58) – (60) следует, что L_z < L (как и должно быть), но две другие проекции не определены. Поэтому вектор в квантовой физике – это не обычный вектор, заданный модулем и направлением (или тремя проекциями), а нечто более сложное: это вектор, «прецессирующий вокруг направления поля». На рис.13 показаны «конусы прецессии» вектора в состоянии с l =2.

Факт квантования проекции орбитального момента импульса был подтвержден экспериментально (см.§14).

Электронные облака в возбужденных состояниях имеют подчас самую причудливую форму, зависящую от значений всех трех квантовых чисел (тороиды, многолепестковые фигуры и т.п.)