Лекция 30.04.2020 г.

Примеры решения уравнения Шредингера

1. Туннельный эффект

Туннельным эффектом называется прохождение микрочастицы через потенциальный барьер в том случае, когда полная энергия Е частицы меньше высоты барьера (рис.5.1, а).

Рис.5.1

В классической теории это невозможно. Если классическая частица с энергией , скользя без трения, повстречает горку высоты (рис.5.1, б), то, поднявшись до точки поворота П, в которой вся ее кинетическая энергия перейдет в потенциальную, частица повернет обратно. Кинетическая энергия не может быть отрицательной, и потенциальный барьер не будет преодолен.

Тем не менее, на практике квантовый туннельный эффект встречается так часто, что о его природе обычно не задумываются.

Пример: металл, находясь в воздухе, всегда покрывается окисной пленкой, которая является хорошим диэлектриком. Такая пленка образует потенциальный барьер для электронов, создающих электрический ток. Большая часть этих электронов имеет энергию, недостаточную для преодоления этого барьера. Поэтому по классическим законам протекание тока через окисленную поверхность металла (вилку, включенную в розетку) сильно затруднено. Тем не менее ток возникает благодаря туннельному переходу электронов сквозь окисную пленку.

Рис.5.2

Покажем, что уравнение Шредингера допускает туннельный эффект. Пусть частица с массой m и энергией Е движется вдоль оси х и налетает на потенциальную ступеньку (область, в которой потенциальная энергия частицы постоянна и ).

Это происходит, например, при движении свободного электрона с энергией Е в металле (рис.5.2). Существование двойного электрического слоя на границе металла приводит к тому, что потенциальная энергия электрона вне металла возрастает на величину , где – работа выхода электрона из металла. Классический электрон оказаться вне металла в области не может (рис.5.2) и вылетает из металла только за счет фотоэффекта, поглощая фотон с энергией .

Рис.5.3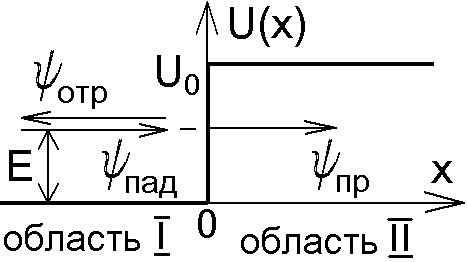

К потенциальной энергии можно добавить или вычесть любую постоянную величину. Поэтому совместим начало координат со ступенькой и будем считать, что в области I потенциальная энергия падающей на ступеньку частицы равна нулю (рис.5.3).

Уравнение Шредингера (4.35) для частицы запишется в виде:

(5.1)

если ввести положительные константы и .

Решения уравнений (5.1) известны:

(5.2)

где A, B, C, F – постоянные интегрирования.

Физический смысл полученных решений (5.2) очевиден, если подставить выражение кинетической энергии . Тогда в классически разрешенной области I имеем . Сравнивая с формулой (4.16), видим, что волновая функция описывает свободную частицу, летящую вдоль оси х, т.е. падающую на ступеньку. Волновая функция соответствует частице, летящей против оси х, т.е. отраженной от ступеньки.

Волновая функция опишет состояние частицы, прошедшей в классически запрещенную область II (классическая частица в этой области существовать не может, так как ее импульс будет мнимым). Постоянную интегрирования F приравниваем нулю из граничного условия (вероятность обнаружения частицы в области не может быть бесконечной).

Рис.5.4

Коэффициентом прохождения или вероятностью преодоления потенциального барьера называется отношение потока прошедших частиц к потоку падающих

. (5.8)

Для прямоугольного барьера на рис.5.4

. (5.9)

Рис.5.5

Если потенциальный барьер имеет произвольную форму, то разобьем его на n очень узких прямоугольных барьеров шириной и высотой каждый (рис.5.5). Поток частиц, прошедших через узкий прямоугольный барьер, будет потоком частиц, падающих на следующий узкий барьер. Поэтому коэффициент прохождения через все барьеры согласно формуле (5.8) окажется произведением коэффициентов прохождения через каждый из барьеров:

.

Показатели экспонент в сомножителях (5.9) при этом складываются и при дают интеграл:

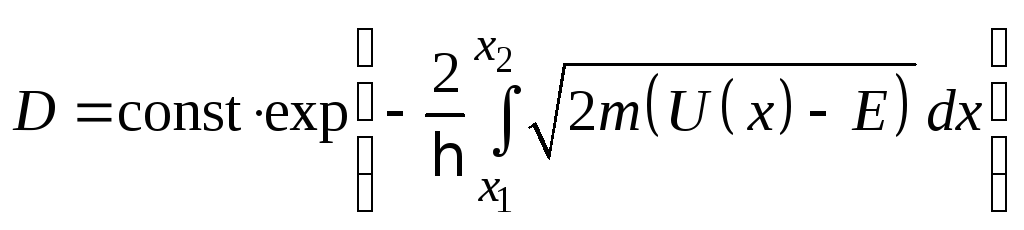– (5.10)

– это вероятность туннельного преодоления падающей микрочастицей с массой m и энергией Е потенциального барьера произвольной формы.

Формула (5.10) является приближенной, так как получена с точностью до постоянного множителя, зависящего от формы барьера. Но главным результатом будет экспоненциальная за- висимость коэффициента D от толщины и высоты барьера и от массы частицы.