Лекция 28.05.2020 г. (2 курс)

Полупроводники и ферромагнетики

§1. Собственная проводимость полупроводников

Полупроводниками называются вещества, проводимость которых в 10⁶ раз хуже, чем у металлов и растет с ростом температуры (а у металлов, как известно, падает). К чистым (истинным) полупроводникам с собственной проводимостью относятся элементы четвертой группы периодической системы, а именно: германий, кремний и серое олово. Энергетический спектр соответствующих кристаллов такой же, как у алмаза. На рис.30 показаны спектры алмаза и германия при Т = 0. Видно, что вся разница – в ширине запрещенной зоны, отделяющей валентную зону от пустой.

У германия вследствие малости ширины запрещенной зоны часть электронов из валентной зоны под действием термического возбуждения может перескакивать в пустую зону (то же у Si и Sn).

В результате этого в пустой зоне концентрация свободных электронов достигает значений n ~ 10¹⁵10¹⁶ м^–3 (при нормальной температуре), и пустая зона становится зоной проводимости. Очевидно, что с ростом Т концентрация свободных носителей, а, значит, и проводимость кристалла возрастают.

На месте ушедшего из валентной зоны электрона остается вакантный энергетический уровень, на который могут переходить другие электроны валентной зоны. Т.о. электроны валентной зоны получают возможность перемещаться под действием внешнего электрического поля, т.е. участвовать в электропроводности. Но их поведение существенно отличается от поведения свободных электронов, т.к. на их движении заметно сказывается поле ионной кристаллической решетки. В результате совместного действия двух полей (внешнего и поля решетки) электроны, находящиеся вблизи крыши валентной зоны, ускоряются в направлении, противоположном действующей внешней электрической силе, т.е. при наложении внешнего поля их импульс уменьшается. Поэтому, если рассматривать их как свободные частицы, то нужно приписать им отрицательную эффективную массу.

Вообще говоря, понятие эффективной массы очень удобно, т.к. позволяет свести движение связанных частиц к движению свободных. Если речь идет о классических частицах, то введение эффективной массы означает переход от уравнения

(102)

к уравнению

(103)

где m^* и есть эффективная масса. Она может принимать любое положительное и отрицательное значения. Аналогично можно поступить и в случае квантовых частиц.

Как уже говорилось, все электроны кристалла испытывают в той или иной мере воздействие со стороны поля ионной решетки, поэтому во всех формулах для проводимости твердых тел под m_e следует подразумевать не обычную массу электрона, а его эффективную массу. Другое дело, что для электронов металла m^* почти не отличается от m_e; для электронов зоны проводимости полупроводника m^* > 0, а для электронов валентной зоны m^* < 0.

Однако, вернемся к этим электронам.

Удобно ввести в теорию квазичастицу с эффективной массой m_p = – m^* и зарядом q_p = + e. Такую квазичастицу называют дыркой.

Можно показать, что если в валентной зоне имеется одна вакансия, то ток всех электронов валентной зоны равен току одной дырки. Поэтому говорят, что при переходе одного электрона из валентной зоны в зону проводимости на его месте возникает одна дырка. Т.о. число электронов в зоне проводимости истинного полупроводника равно числу дырок в валентной зоне, т.е. n_p = n_e.

Т.к. электронный и дырочный газы в полупроводнике невырожденные, то, например, для электронов распределение по энергиям можно записать в виде

(104)

г

де за нулевой уровень энергии принято дно зоны проводимости (рис.31).

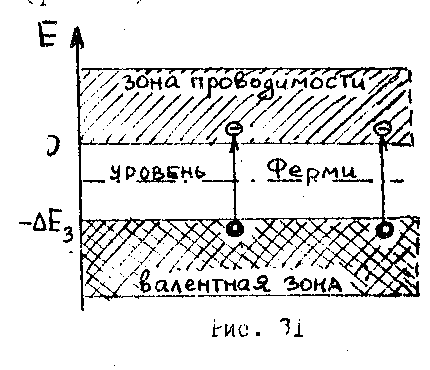
Аналогично запишется распределение дырок в валентной зоне. Вычисляя

(105)

и n_p и приравниваем их, находим:

(106)

Следовательно уровень Ферми в чистых полупроводниках лежит посередине запрещенной зоны. Т.о. изформул (105) и (106) вытекает, что

(107)

Т.к. проводимость чистого полупроводника (собственная проводимость) состоит из суммы проводимостей электронов и дырок, а каждая из них пропорциональна n_e, то окончательно получаем

(108)

Значит, собственная проводимость полупроводника экспоненциально растет с ростом температуры.