2_1matmod

Верификация – это проверка того, что включенные в модель формальные соотношения правильно отражают выбранную концепцию, что они не имеют внутренних противоречий и несоответствий в размерности, что предусмотренные математические преобразования не содержат ошибок и программа составлена правильно.

Прежде чем переходить к работе с моделью, необходимо убедиться в ее корректности и правильном функционировании всех алгоритмов и программ модели. Для этого нужно выполнить отладку программы и провести независимое тестирование. Проверяется возможность появления абсурдных результатов (например, отрицательной концентрации или численности популяции) при достижении предельных значений парfметров.

Верификация тест на внутреннюю логику модели. Типичный вопрос на этапе верификации: Ведет ли себя модель так, как ожидалось? Этот вопрос предполагает, что мы знаем некоторые реакции реальной системы на воздействия и на этом этапе проверяем, воспроизводит ли их модель.

10 шаг- анализ чувствительности

На этом этапе проверяют чувствительность представляющих наибольший интерес переменных состояния модели к изменениям начальных условий, параметров, структуры модели, внешних переменных и управляющих функций.

•Анализ чувствительности помогает определить ключевые моменты функционирования системы в контексте изучаемой проблемы и установить исследовательские приоритеты.

•Анализ чувствительности показывает пути совершенствования модели, путем уточнения параметров и изменения ее структуры.

•Результаты анализа чувствительности полезны при верификации, калибровке и проверке модели.

Известно много различных методов анализа чувствительности, которые классифицируют как

математические и графические.

Математические методы основаны на вычислении выхода (интересующей переменной состояния) для разных значений входа.

Графические методы характеризуют чувствительность выхода к изменениям входа в форме графиков. Как правило, они используются в качестве дополнения к математическим методам.

Если модель имеет модульную структуру, то анализ чувствительности может проводиться для разных модулей отдельно, но с учетом взаимодействия модулей.

Нельзя сказать какой из методов анализа чувствительности является лучшим. У каждого есть свои достоинства и ограничения. Выбор метода зависит от типа модели и задач исследования. Рекомендуется использовать два или большее число разных методов.

11 шаг- калибровка (подбор значений параметров).

Калибровка - это попытка найти лучшее соответствие между расчетными и наблюдаемыми данными путем варьирования значений некоторых параметров.

Для некоторого набора значений параметров вычисляются значения переменных состояния, которые сравниваются с их экспериментальными оценками. Выбирают тот набор значений параметров, который дает наименьшие расхождения с экспериментальными значениями.

Необходимость в калибровке вызвана следующими причинами:

1.Данные, получаемые в результате экспериментальных исследований или натурных наблюдений, включают различные ошибки измерений. Модель, основанная на них, может давать результаты, отличные от реальных, именно за счет ошибок в определении исходных данных.

2.Для многих параметров не известны их точные значения, а задаются лишь интервалы значений, поэтому имеет место неопределенность при выборе конкретного значения параметра модели.

3.Все модели являются упрощением реальности и не учитывают все детали. Влияние неучтенных отношений может быть принято в расчет в результате калибровки. Калибровка позволяет свести к минимуму расхождения модельного выхода и результатов наблюдений. А имеющиеся различия, может быть, объясняются пропущенными в модели деталями.

12 шаг- проверка адекватности модели

Под адекватностью математической модели понимается степень соответствия результатов моделирования экспериментальным данным, характеризующим изучаемую систему.

На этом этапе проверяется способность модели решать поставленные при ее создании задачи.

Положительный результат проверки не является доказательством того что модель заключает в себе абсолютную истину, а лишь демонстрирует ее пригодность для использования.

Не существует универсального критерия проверки адекватности моделей сложных систем. Поэтому следует проверять модель по комплексу критериев. Для проверки моделей используются качественные, графические, статистические методы.

Предложено множество различных количественных показателей адекватности модели, например:

•максимальная относительная ошибка

•коэффициент несовпадения Тейла

•средняя относительная ошибка

Заключительный синтез

Принцип итеративности. На каждом из этапов могут возникать трудности, для преодоления которых необходимо перестраивать модель, например, расширять список переменных состояния, уточнять форму используемых соотношений для описания взаимодействий между переменными и др. По существу создание модели включает путь последовательных приближений, в процессе которых получается новая информация об объекте моделирования, усовершенствуется система наблюдений и экспериментов, проверяются гипотезы о механизмах изучаемых процессов.

На заключительном этапе нужно:

•обозначить область применения модели;

•представить содержательные результаты;

•показать в каком направлении модель следует развивать в дальнейшем.

11.Источники неопределенностей в почвенных и экологических моделях. Природная вариабельность объекта исследования. Ошибки, возникающие при определении структуры модели, выборе сценария и оценке параметров.

Так как модель всегда является упрощенным представлением реальности, любое предсказание имеет неопределенность. Неопределенности обусловлены, как природной вариабельностью моделируемых явлений, так и ошибками, сделанными в процессе определения качественной и аналитической структуры модели, при оценке параметров и выборе ситуаций, для которых модель будет реализована. Ошибки, возникающие на разных этапах построения и реализации модели не являются независимыми, а могут взаимодействовать самым неожиданным образом,

увеличивая неопределенность предсказаний. Выделяют следующие источники неопределенностей в соответствующих моделях: обусловленные неполнотой моделей, неадекватностью моделей и неопределенностью исходных параметров.

Ошибки, возникающие при определении структуры модели

При определении структуры модели возникает проблема выбора числа компонентов модели. Оно зависит от цели моделирования и выбранного масштаба. Нужно помнить, что ошибки динамических моделей заметно возрастают уже при агрегировании переменных, различающихся по скоростям оборота более чем в три раза (Gardner et al., 1982).

Выбор уровня сложности модели, который минимизирует ошибки предсказаний, является непростой задачей, так как при увеличении детальности описания особенно за счет включения процессов, параметры которых трудно измерить, возрастает неопределенность модельных предсказаний. Лучшим подходом в этих обстоятельствах является построение серий последовательно усложняющихся моделей. Этот способ реализует два методологических принципа системного анализа: принцип итеративности, состоящий в последовательном совершенствовании модели, и принцип соответствия сложности и точности. В результате построения серии получают модель минимальной сложности для заданной точности экспериментальных данных.

Ошибки, возникающие при выборе сценария

Неопределенность модельных предсказаний значительно возрастает, когда модели применяются к областям большим, чем их внутренний масштаб.

Например, когда локальные (точечные) модели, при построении которых исходили из предположения о гомогенности климатических и почвенных условий в пределах единичной площади, применяются в региональном масштабе. В этом случае важно оценить как отказ от предположения о пространственной однородности внешних условий сказывается на ошибках моделирования.

Как известно, для нелинейных функций значение функции, определенное по среднему значению аргумента не равно среднему значению функций, определенных раздельно для каждого из значений аргументов. Следовательно, ошибки моделирования при переходе от локального к региональному масштабу будут возрастать в тех случаях, когда модель содержит нелинейные функции от изменяющихся в пространстве входных переменных. Ошибки агрегирования зависят не только от степени нелинейности, используемых в модели функций, но и от пространственного масштаба агрегирования.

Ошибки, связанные с оценкой параметров

Для исследования зависимости предсказаний от точности значений параметров широко применяется анализ чувствительности.

Показатели чувствительности представляют собой производную интересующего модельного предсказания (переменной отклика) по параметру.

Анализ чувствительности позволяет выявить параметры, к которым переменная отклика наиболее чувствительна. Для уменьшения ошибок моделирования эти параметры следует определять наиболее точно. Анализ чувствительности показывает также путь усложнения модели в тех случаях, когда ее адекватность недостаточна. Усложнять модель целесообразно путем уточнения описания тех процессов, к параметрам которых модель наиболее чувствительна.

Исследование неопределенности предсказаний позволяет определить пути совершенствования моделей.

12.Статические биогеохимические модели. Их достоинства и недостатки. Энвирон-анализ.

Статические модели не рассматривают изменения системы во времени. Статические биогеохимические модели относятся к классу компартментальных (В компартментальной модели каждому компартменту соответствует переменная состояния ( концентрация, масса, давление жидкости или газа), концептуально-

балансовых моделей, отражающих законы сохранения вещества. (Основы методологии построения таких моделей заложены в работах Г. Одума(1961), Дж. Форрестера (1961), А.А. Ляпунова и Яблонского (1963), А.А. Ляпунова и А.А. Титляновой (1971), Н.И.Базилевич (1978). Статические модели характеризуют усредненные по времени ситуации.)

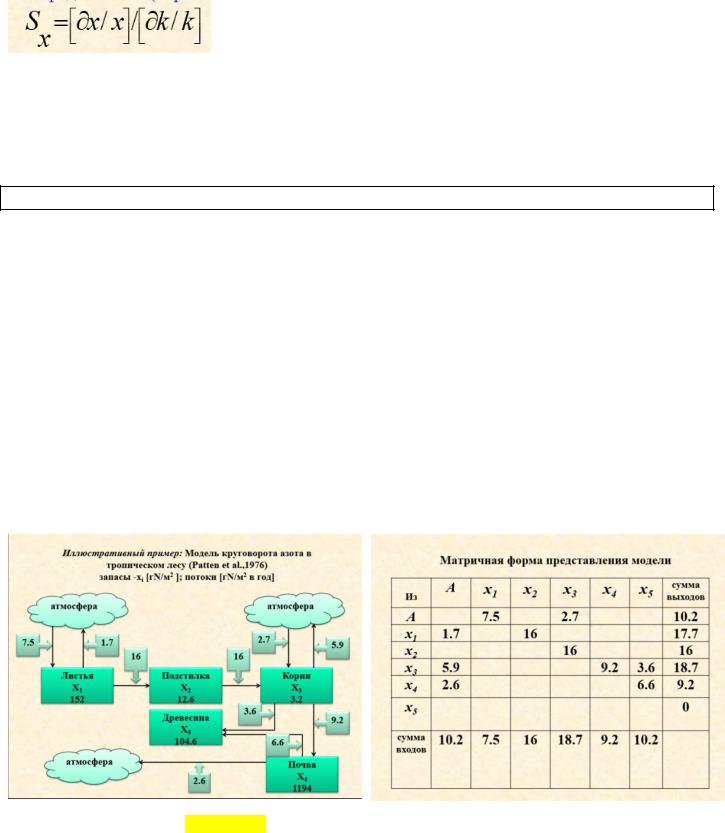
При построении таких моделей система разбивается на блоки (компартменты), содержащие определенные запасы вещества и обменивающиеся им между собой и окружающей средой. На основе экспериментальных данных определяются запасы вещества в выделенных блоках, скорости обмена между ними, а также скорости входных и выходных потоков. Модель представляют в виде численной потоковой диаграммы с указанием запасов и скоростей потоков.

Достоинства статических биогеохимических моделей

При их построении, как правило выявляют недостаточно изученные звенья круговорота вещества в экосистемах, что позволяет использовать их как эффективный инструмент планирования исследований. Такие модели, несмотря на их схематичность и известную условность, могут быть полезны для описания квазистационарных состояний или для описания усредненной по времени ситуации. Они могут служить эталоном - точкой отсчета для мониторинга окружающей среды.

Недостатки статических биогеохимических моделей

Статический характер, они отражают только среднюю картину круговорота вещества в экосистемах за определенный временной интервал.

ЭНВИРОН-АНАЛИЗ. В конце 70-х - начале 80-х годов прошлого века был предложен метод анализа компартментальных моделей, получивший название энвирон-анализа (Patten, 1982; Patten, 1985).

ЭНВИРОН - совокупность тех блоков и потоков между ними, с которыми рассматриваемый блок связан либо непосредственно, либо через другие блоки.

ВХОДНОЙ ЭНВИРОН - совокупность блоков, выходы из которых рано или поздно поступят на вход рассматриваемого блока вместе с соответствующими потоками

ВЫХОДНОЙ ЭНВИРОН - совокупность блоков, в которые рано или поздно поступит частица вещества, прошедшая через рассматриваемый блок вместе с соответствующими потоками.

Используя матричные соотношения этого метода, можно вычислить, какая доля выходящего из i-го компартмента потока попадает в j-й, оценить среднее время, проводимое веществом в компартменте, сделать количественные выводы о роли того или иного процесса в функционировании экосистемы.

Энвирон-анализ предлагает исследование только лишь стационарного состояния системы, поскольку одним из его исходных требований является постоянство потоков и запасов вещества.

13. Динамические модели. Используемый математический аппарат. Фазовое пространство. Фазовая траектория. Фазовый портрет. Стационарное состояние системы.

Динамическими системами называют любые системы (физические, химические, биологические, экономические, социальные и.др.), состояние которых изменяется во времени дискретно или непрерывно.

В математическом понимании динамической системой является любой объект, для которого однозначно определено понятие состояния, как совокупности некоторых величин в данный момент времени, и задан закон, который описывает изменение начального состояния с течением времени (Анищенко,2008).

Почва относится к динамическим системам. Функционирование почвы, как целостной системы, является результатом взаимодействия составляющих ее компонентов. Понять динамические свойства почвы можно на основе системного подхода, анализируя поведение каждого из ее компонентов, как результат его

взаимодействия с другими компонентами.

Одним из наиболее эффективных методов изучения изменений почв с течением времени является построение и анализ динамических моделей. Анализ динамических свойств моделей, характеризующих разные аспекты функционирования почв, позволяет лучше понять особенности ее динамики. Для описания динамических систем используются различный математический аппарат (дифференциальные уравнения, дискретные отображения, теория марковских цепей и др.).

В настоящем курсе мы рассмотрим динамические модели, представленные дифференциальными уравнениями. Математический язык дифференциальных уравнений для описания динамических систем был предложен Исааком Ньютоном (1642-1727). В настоящее время он широко используется при построении моделей в самых разных областях науки.

Приведем некоторые основные понятия теории обыкновенных дифференциальных уравнений и рассмотрим несколько примеров простейших моделей обсуждаемого типа. Для того чтобы определить динамическую

систему, модель которой мы хотим построить, нужно задать конечное число переменных, однозначно характеризующих ее состояние.

Предположим, что в соответствии с поставленной проблемой, для характеристики состояния почвы выбрано n различных компонентов. Каждый i компонент характеризуется переменной состояния xi. В качестве переменных состояния могут быть выбраны концентрации различных веществ, численность микроорганизмов, и др. Закон изменения динамической системы во времени можно в общем виде представить системой n дифференциальных уравнений:

Особый интерес представляет случай системы (1), когда правые части не зависят явно от переменной t:

такие системы называются автономными.

Динамические модели этого вида получили широкое распространение в почвоведении и экологии. Решение системы представляет собой совокупность функций, характеризующих зависимость переменных состояния от времени:

х 1(t), х 2(t),….. х i(t),….. х n(t)

Лишь для небольшого класса систем дифференциальных уравнений удается найти аналитическое решение, то есть представить зависимость переменных состояния от времени в виде явно заданных математических формул. В большинстве случаев получают только численное решение.

В процессе изменения состояния системы во времени переменные хi изменяются согласно системе уравнений (2). В момент времени t каждому состоянию

системы соответствует совокупность n значений переменных

хi(t).

Для удобства анализа поведения динамических систем во времени используют понятие n- мерного фазового пространства - абстрактного пространства с осями

координат х1, х2,... хi,… хn..

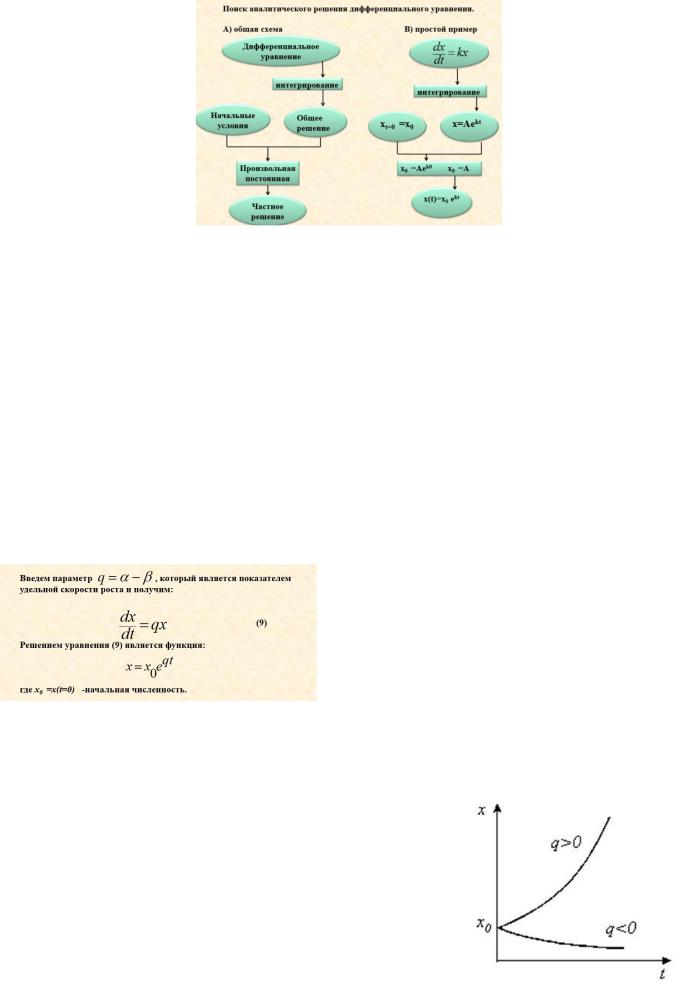
Эта простая линейная модель демонстрирует одно из важнейших свойств математических моделей — их универсальность, т. е. их применимость к объектам принципиально различной природы.

Пример: Модель Мальтуса (модель экспоненциального роста численности популяции).

Модель предложена Мальтусом (1766-1834) в 1798 г. в его классической работе «О законе роста народонаселения». Мальтус –известный английский демограф и экономист, обратил внимание на тот факт, что численность популяции растет по экспоненте ( в геометрической прогрессии), в то время как производство продуктов питания растет линейно ( в арифметической прогрессии), из чего сделал справедливый вывод, что рано или поздно экспонента обязательно обгонит линейную функцию и наступит голод.

В основу модели положено простое утверждение, что скорость изменения численности населения со временем t пропорциональна его текущей численности x(t), умноженной на сумму коэффициентов рождаемости и смертности:

Эта модель не учитывает зависимости сложнейшего процесса изменения численности населения от множества условий и подходит только для описания изменения численности изолированной популяции, которая развивается в условиях неограниченных ресурсов. Например, динамики популяции простейших организмов, выращиваемых в культиваторе в условиях избытка пищи.

Экспоненциальный рост. Зависимость численности популяции от времени

Модель экспоненциального роста используется для описания широкого круга явлений (радиоактивный распад, динамика популяций,

разложение растительных остатков, минерализация гумуса, рост зарплаты и др.).

На первый взгляд кажется, что между ними нет ничего общего. Однако описание всех этих разнородных явлений основано на одном общем предположении, что скорость изменения значения переменной состояния пропорциональна самому ее значению. Это предположение используется в различных областях знаний, а приведенный пример демонстрирует универсальность моделей, то есть их применимость для описания объектов различной природы.

Простейшая линейная динамическая модель открытой системы

В качестве еще одного примера динамической модели рассмотрим простейшую линейную модель открытой системы, в которой происходит обмен веществами «а» и «b» с окружающей средой и обратимая реакция первого порядка превращения a↔b.

Они не зависят от начальных условий, то есть от значений переменных a и b в момент времени t=0. Это означает, что при каком бы начальном состоянии система не находилась, в ней со временем установится стационарный режим.

Хотя начальные условия не влияют на стационарные значения, они определяют характер кривых, описывающих изменения переменных состояния при переходе от начального состояния при t=0 к стационарному при t→∞.

На примере этой модели А.Б Рубин (1998) показал, что даже такая, до предела упрощенная, модель отражает основные черты совокупности метаболических реакций клетки как открытой системы. Она может быть использована для описания обменных процессов и в других открытых системах, например, в почве, что

является еще одной демонстрацией универсальности математических моделей.

Если модели, описывающие различные объекты, основаны на одинаковых предположениях, то для их описания могут быть использованы одни и те же математические выражения. Как отмечал великий французский математик Анри Пуанкаре : "Математика - это искусство давать разным вещам одно

наименование".