6. Принципы использования гармонического анализа для обработки диагностических данных

Многочисленные процессы, обуславливающие жизнедеятельность организма, носят периодический характер (сердечные сокращения, дыхание, кровенаполнение сосудов и т.д.). Диагностические данные, позволяющие судить о работе ряда органов и функциональных систем организма, представляется в виде периодических кривых. Например, электрокардиограмма (ЭКГ) представляет собой зафиксированную на бумажной ленте или на экране монитора сложную периодическую зависимость от времени tбиопотенциалов, сопровождающих работу сердца ( см. рис.7). -

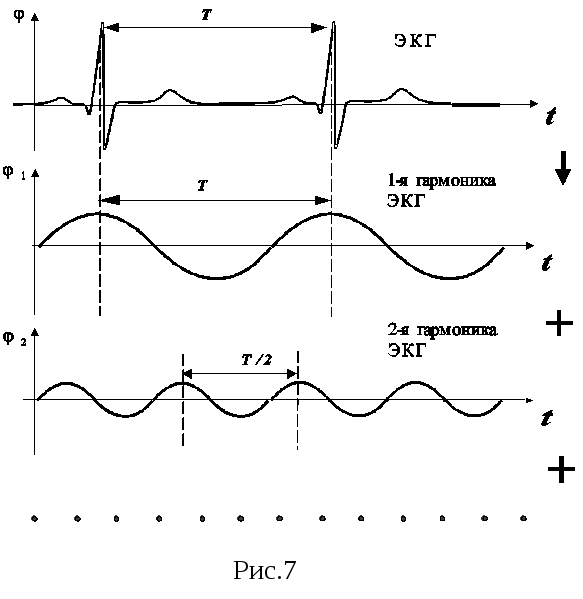
Механизмы генерации этих потенциалов и их распространения будут рассмотрены в других разделах курса. Здесь отметим только, что обработка данных ЭКГ может быть произведена с помощью гармонического анализа. С помощью специальных приборов - анализаторов получают гармонический спектр ЭКГ. Частота первой гармоники в этом спектре соответствует частоте сердечных сокращений у пациента. Она составляет около1 Гц (периодТ порядка1с). Из вида реально полученных спектров следует, что гармоники ЭКГ с частотами свыше150-400 Гц имеют пренебрежимо малую амплитуду и для анализа ЭКГ ряд Фурье (формула (22)) можно ограничить (с запасом) последней составляющей с частотой400 Гц. Это означает, что информация об электрической деятельности сердца заключена в частотном диапазоне от 0,5 Гц ( минимально возможная частота сердечных сокращений) до400 Гц (частота гармоники самого высокого порядка).

Полученный результат предъявляет необходимые требования к аппаратуре регистрации ЭКГ: она должна обеспечивать одинаковым образом съем, усиление и отображение электрических сигналов в указанном частотном диапазоне. Так, с одним и тем же коэффициентом усиления должны усиливаться составляющие ЭКГ-сигнала на всех частотах, представленных в его гармоническом спектре; регистрирующие устройства должны обладать одинаковой чувствительностью для этих составляющих. Только при этом условии зарегистрированная ЭКГ в точности повторяет реальную зависимость биопотенциалов, вызванных работой сердца, от времени.

Применение гармонического анализа для обработки данных о периодических физиологических процессах позволяет с помощью электронной и вычислительной техники автоматизировать диагностику заболеваний и существенно расширить ее возможности.

7. Механические волны

Механическая волна представляет собой процесс распространения механических колебаний в пространстве. Из-за наличия упругих связей между частицами среды перемещения одной из частиц при возникновении колебаний вызывает движение соседних частиц - этот процесс распространяется в пространстве с некоторой скоростью.

Волна называется продольной , если направление перемещения частиц среды совпадает с направлением распространения волны. Если эти направления взаимноперпендикулярны, то такая волна называетсяпоперечной. Продольные механические волны могут распространяться в любых средах (кроме вакуума), а поперечные - только в твердых телах.

7.1. Уравнение волны

Рассмотренные выше математические выражения, описывающие характер колебаний, определяют смещение как функцию одной переменной - времени. Смещение S в волне зависит уже от двух переменных - времениtи пространственной координатых- и обладает поэтому двойной периодичностью.

Для получения уравнения волны , то есть аналитического выражения функции двух переменныхS = f (t,x), представим что, в некоторой точке пространства возникают гармонические колебания с круговой частотой и начальной фазой, для упрощения равной нулю (см. рис.8). Смещение в точкеМ :S_м = A sin t, гдеА- амплитуда. Поскольку частицы среды, заполняющие пространство, связаны между собой, то колебания от точкиМраспространяются вдоль осих со скоростьюv. Через некоторое времяtони достигают точкиN. Если в среде отсутсвует затухание, то смещение в этой точке имеет вид:S_N = A sin  (t - t), т.е. 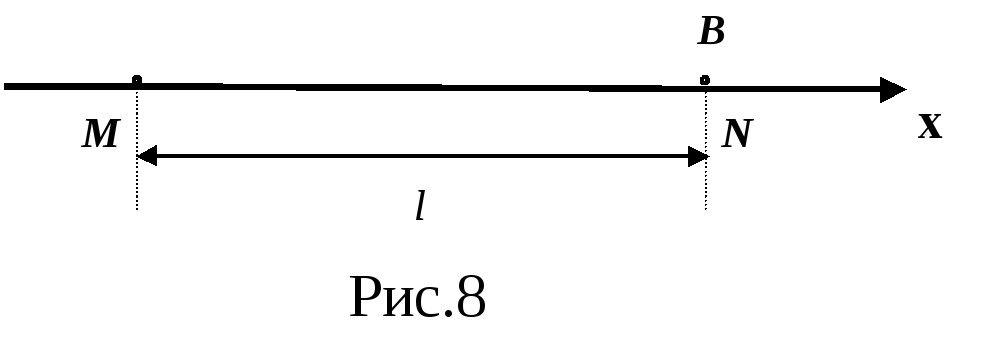колебания запаздывают на времяt относительно точкиM .Поскольку, то заменив произвольный отрезокMN координатойх , получимуравнение волныв виде:

(23)

Учитывая, что (гдеТ -период), а длина волны = v T, формулу (23) можно записать в виде:

(24)

Уравнение волны (23) или (24) позволяет определить в любой момент времени tсмещение любой точки, имеющей координатух.