Часть I механические колебания и волны

Колебаниями называют движения или изменения состояния, повторяющиеся через определенные промежутки времени.

1. Гармонические колебания

Простейшим видом колебательного движения являются гармонические колебания, когда колеблющаяся величина изменяется со временем по закону синуса или косинуса.

1.1. Дифференциальное уравнение гармонических колебаний и его решение

Покажем, что гармоническое колебание возникает под действием упругой силы.

Представим материальную точку массойm, закрепленную на пружине жесткостик и расположенную на абсолютно гладкой горизонтальной поверхности (см. рис. 1). Если растянуть пружину на расстояниех ,то со стороны пружины на эту точку действует упругая силаF_y , пропорциональная смещению хпо закону Гука:

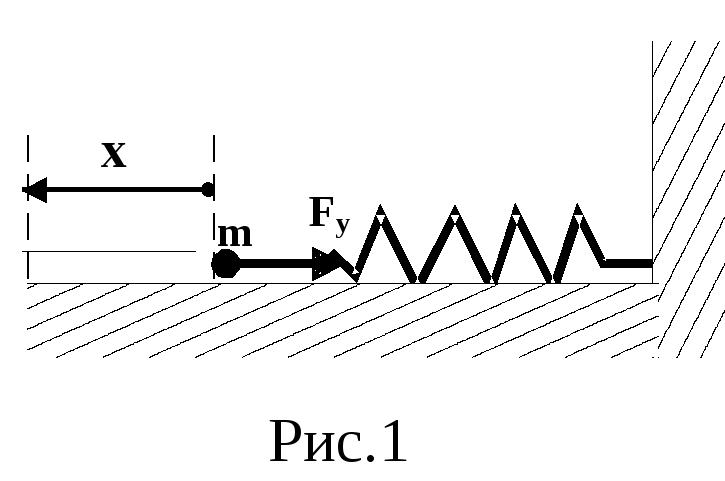
F_y = - кх.

Знак “минус” указывает на противоположность направлений смещения и действия силы упругости.

Чтобы установить характер движения, т.е. зависимость х = f(t),запишем для этого случая дифференциальное уравнение, считая что в рассматриваемой системе движение определяется только наличием силы упругости:

= -кх. (1)

Разделим левую и правую части уравнения (1) на m и обозначим отношение положительных величинк и m через₀² :

или .(2)

Решение дифференциального уравнения (2) имеет вид:

х = А₀ sin (₀ t + ₀ ) (3)

и показывает, что при наличии в системе лишь силы упругости движение совершается по гармоническому закону. Величина , представляет собой циклическую частоту колебаний,А₀ - амплитуду,₀ - начальную фазу, (₀ t +  ) - фазу колебаний. Период колебаний, а частота =1/ Т.

Зависимость скорости (v) движения материальной точки от времени при гармоническом колебаниинайдем, взяв производную по времени от формулы (3):

(4)

Из сравнения выражений (3) и (4) видно, что смещение и скорость гармонического колебания различаются по фазе на /2: скорость максимальна при прохождении точкой положения равновесия (смещение равно нулю), наоборот, при максимальном смещении (равном амплитуде) скорость равна нулю.

Выражение для ускорения получается дифференцированием формулы (4):

(5)

Из формулы (3) следует, что смещение и ускорение изменяются в противофазе.

1.2. Энергия гармонического колебания

Полная энергия гармонического колебания Еопределяется суммой кинетическойЕ_к и потенциальнойЕ_п энергии:

(6)

Подставляя в формулу (6) выражение для скорости из (4), а для смещения - из (3) и учитывая, что к = ₀² m, получим:

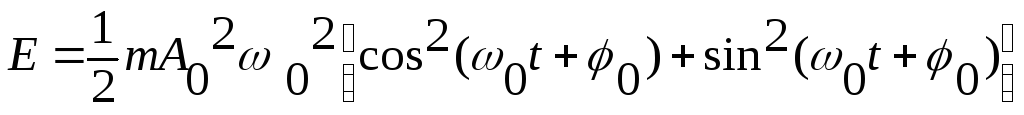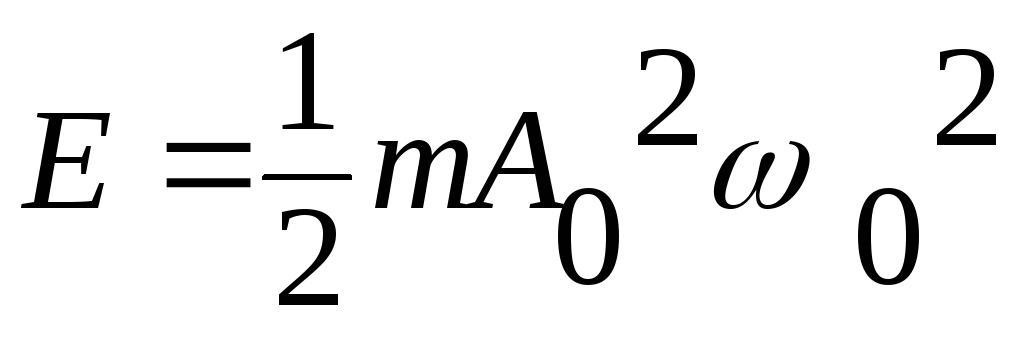или. (7)

Из формулы (7) следует, что энергия гармонического колебания прямо пропорциональна квадрату амплитуды. Этот вывод достаточно тривиален - чем больше “размах” колебаний, тем больше и их энергия. Кроме того, энергия сильно зависит и от круговой частоты колебаний - прямо пропорционально квадрату ее значения.

2. Затухающие колебания

2.1. Дифференциальное уравнение затухающих колебаний и его решение

В реальных системах всегда существуют некоторые силы сопротивления, препятствующие развитию колебательных процессов. Для установления характера колебательного движения в этом случае будем считать, что наряду с упругой или квазиупругой силой F_y в системе действует сила трения, пропорциональная скорости и направленная противоположно ей:F_тр=. Тогда учет влияния этих двух сил на характер движения приводит к следующему дифференциальному уравнению:

(8)

Разделив левую и правую части уравнения (8) на m ,обозначивr/m = 2 и сохранив обозначениек/m =₀² , приведем это уравнение к виду:

(9)

Решение этого уравнения имеет вид:

(10)

Формула (10) представляет собой смещение при затухающем колебании как функцию времени и параметров системы  и. Коэффициент = r/2m имеет смысл коэффициента затухания. Из формулы (10) видно, что в затухающих колебаниях амплитуда уменьшается со временем. Причем, колебания затухают тем быстрее, чем больше коэффициент затухания.По сравнению с гармоническими колебаниями уменьшается также и циклическая частота колебаний. Это уменьшение зависит от коэффициента затухания. Оказывается, что

(11)

Колебательный процесс может происходить лишь при условии: (₀² -  ²)>0,когда частота в формуле (11) является действительной величиной . Если же затухание в системе слишком велико(₀ <  ), то под корнем в формуле (11) оказывается отрицательная величина, - в этом случае движение не имеет периодического характера.

Графически затухающее колебания представлено на рис.2, где сплошной линией показана зависимость смещения от времени, а пунктирной - экспоненциальный закон убывания амплитуды.