2.2. Декремент затухания и логарифмический декремент затухания

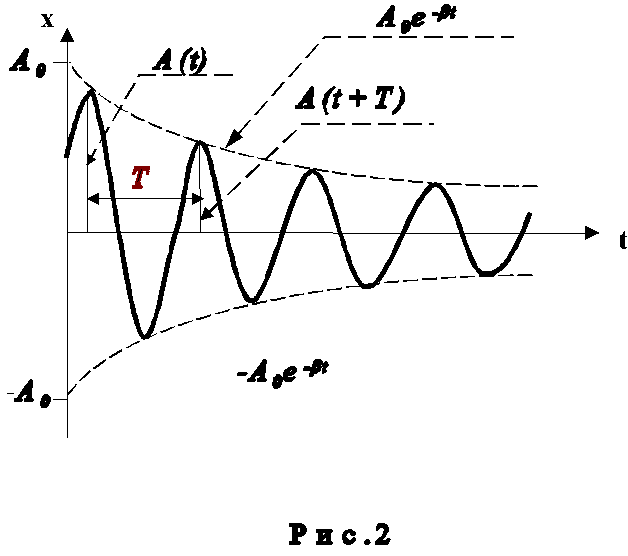
Уже указывалось, что быстрота убывания амплитуды затухающих колебаний характеризуется коэффициентом затухания  , который зависит от параметров системы. На практике затухание колебаний удобнее характеризоватьдекрементом затухания , представляющимсобой отношение двух последовательных амплитуд, разделенных периодом колебаний Т(см. рис.2) :

Натуральный логарифм этого отношения, называемый логарифмическим декрементомзатухания  , весьма просто связан с коэффициентом затухания и периодом:

или =  T . (12)

Удобство использования логарифмического декремента затухания  для характеристики затухающих колебаний заключается в простоте его экспериментального определения. Если затухающие колебания зарегистрированы в виде соответствующего графика (см.рис.2), то необходимо в любых единицах измерить две амплитуды колебаний, разделенные интервалом времени, равным периоду, и найти натуральный логарифм их отношения. Определив таким образом величину и зная периодТ, легко найти и коэффициент затухания.

3. Вынужденные колебания

3.1. Дифференциальное уравнение вынужденных колебаний и его решение

Рассмотрим теперь случай, когда в системе наряду с силами упругости и трения присутствует некоторая внешняя сила, препятствующая затуханию колебаний. Предположим, что эта вынуждающая сила F_в действует периодически с круговой частотой_в и зависит от времени по закону :F_в = F_оsin_в t , гдеF_о - амплитуда вынуждающей силы.

Для этого случая дифференциальное уравнение (второй закон Ньютона) имеет вид:

(13)

Сохраняя обозначения к / m= ₀² ,r / m = 2, и обозначивF₀ /m = f₀ приведем уравнение (13) к виду:

sin_в t (14)

Решение этого уравнения представляет некоторую функцию, которая графически представлена на рис. 3. Это решение состоит из двух частей. Одна из них соответствует неустановившемуся режиму колебаний, когда их амплитуда зависит от времени. Вторая часть описывает установившийся режим колебаний.

В установившемся режиме вынужденных колебаний смещение х подчиняется гармоническому закону и происходит с частотой, равной частоте действия вынуждающей силы:

х = Аsin( _в t + _o) . (15)

Установившаяся амплитуда А вынужденных колебаний, зависит от параметров системы (частоты собственных колебаний ₀и коэффициента затухания) и от характеристик вынуждающей силы (f₀ и_в):А = f (₀ , , f₀ , _в). Строгое рассмотрение приводит к следующим выражением для значенийА и₀, входящих в формулу (15):

(16)

(17)

Из рассматриваемой формулы (16) следует, что амплитуда достигает максимального значения А_mах при определенном соотношении между величинами₀ , _в и .

Минимум знаменателя в формуле (16) достигается при условии:

 _в=_рез (18)

То есть, амплитуда вынужденных колебаний максимальна, если частота действия вынуждающей силы определяется формулой (18). Явление резкого возрастания амплитуды вынужденных колебаний при частоте действия вынуждающей силы, определяемой формулой (16), называется резонансом.

Если бы затухание в системе отсутствовало ( = 0),то резонанс наступал бы при условии(₀ =  _в) и при этом амплитуда достигала бы бесконечно большого значения.