
- •1. Взаимодействие токов
- •2. Система Си: 1 а
- •3. Вектор магнитной индукции b
- •4. Линии магнитной индукции
- •5. Магнитное поле прямого тока
- •6. Магнитная индукция в центре кругового тока
- •7. Дипольный магнитный момент
- •Формулы для вычисления магнитного момента
- •8. Принцип суперпозиции
- •9. Поток магнитного поля
- •10. *Момент сил, действующих на контур с током в магнитном поле
- •11.*Энергия контура с током в магнитном поле
- •12.*Работа, совершаемая при перемещении тока в магнитном поле
- •13. Магнетики
- •Виды магнитных материалов
- •Области применения магнитных материалов
- •14. Магнитное поле в веществе
- •15. Намагниченность j
- •16.*Токи намагничивания
- •17.*Связь тока намагничивания и намагниченности j
- •18. Напряженность магнитного поля h
- •19. Связь между векторами JиH
- •20. Магнитная восприимчивость
- •21. Связь векторов BиH
- •22. Магнитная проницаемость среды
- •23.*Граничные условия для вектора h
- •24.* Граничные условия для вектора b
- •25. Парамагнетики
- •26. Диамагнетики
- •27. Ферромагнетики
- •28. Домены
- •29. Температура Кюри
- •30. Магнитный гистерезис
- •31. Остаточная индукция
- •32. Коэрцитивная сила
- •33. Явление электромагнитной индукции
- •34. Токи Фуко
- •35.*Правило Ленца
- •36. Явление самоиндукции
- •37. Индуктивность
- •38. Энергия магнитного поля проводника с током
- •39.*Плотность энергии магнитного поля
- •40.*Ток смещения
- •Основные законы
- •1. Закон Био-Савара-Лапласа
- •2. Сила Лоренца
- •3. Закон Ампера
- •4. Теорема Гаусса для магнитного поля в вакууме (инт. И дифф. Вид)
- •5. Теорема о циркуляции для магнитного поля в вакууме (инт. И дифф. Вид)
- •6. Теорема о циркуляции вектора h
- •7. Закон электромагнитной индукции
- •8. **Первая пара уравнений Максвелла (инт. И дифф. Вид)
- •9. **Вторая пара уравнений Максвелла (инт. И дифф. Вид)
- •10. Уравнения электростатики
- •11. Уравнения магнитостатики
- •12. Уравнения Максвелла для электромагнитных волн (инт. И дифф. Вид)
11.*Энергия контура с током в магнитном поле
ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ТОКА
Вокруг проводника с токомсуществует магнитноеполе, которое обладает энергией. Откуда она берется? Источник тока, включенный в эл.цепь, обладает запасом энергии. В момент замыкания эл.цепи источник тока расходует часть своей энергии на преодоление действия возникающей ЭДС самоиндукции. Эта часть энергии, называемая собственной энергией тока, и идет на образование магнитного поля.Энергиямагнитного поля равна собственной энергии тока. Собственнаяэнергиятока численно равна работе, которую должен совершить источник тока для преодоления ЭДС самоиндукции, чтобы создать ток в цепи.
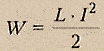
Энергиямагнитного поля, созданноготоком, прямо пропорциональна квадрату силы тока. Куда пропадаетэнергиямагнитного поля после прекращения тока? - выделяется ( при размыкании цепи с достаточно большой силой тока возможно возникновение искры или дуги)
12.*Работа, совершаемая при перемещении тока в магнитном поле
Рассмотрим контур с током, образованный
неподвижными проводами и скользящей
по ним подвижной перемычкой длиной l(рис.
2.17). Этот контур находится во внешнем
однородном магнитном поле![]() ,
перпендикулярном к плоскости контура.
При показанном на рисунке направлении
токаI, вектор
,
перпендикулярном к плоскости контура.
При показанном на рисунке направлении
токаI, вектор![]() сонаправлен
с
сонаправлен
с![]() .
.
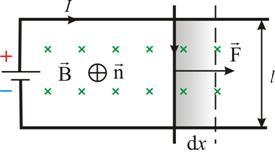
Рис. 2.17
На элемент тока I(подвижный провод) длинойlдействует сила Ампера, направленная вправо:
![]()
Пусть проводник lпереместится параллельно самому себе на расстояние dx. При этом совершится работа:
![]()
Итак,
|
|
|
(2.9.1) |
|
Работа, совершаемая проводником с током при перемещении, численно равна произведению тока на магнитный поток, пересечённый этим проводником.
Формула остаётся справедливой, если проводник любой формы движется под любым углом к линиям вектора магнитной индукции.
Выведем выражение для работы по перемещению замкнутого контура с током в магнитном поле.
Рассмотрим
прямоугольный контур с током 1-2-3-4-1 (рис.
2.18). Магнитное поле направлено от нас
перпендикулярно плоскости контура.
Магнитный поток ![]() ,
пронизывающий контур, направлен по
нормали
,
пронизывающий контур, направлен по
нормали![]() к
контуру, поэтому
к
контуру, поэтому![]() .
.
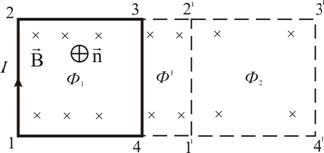
Рис. 2.18
Переместим этот
контур параллельно самому себе в новое
положение 1'-2'-3'-4'-1'. Магнитное поле в
общем случае может быть неоднородным
и новый контур будет пронизан
магнитным потоком ![]() .
.
Площадка 4-3-2'-1'-4,
расположенная между старым и новым
контуром, пронизывается потоком ![]() .
.
Полная работа по перемещению контура в магнитном поле равна алгебраической сумме работ, совершаемых при перемещении каждой из четырех сторон контура:
![]()
где ![]() ,
, ![]() равны
нулю, т.к. эти стороны не пересекают
магнитного потока, при своём перемещение
(очерчивают нулевую площадку).
равны
нулю, т.к. эти стороны не пересекают
магнитного потока, при своём перемещение
(очерчивают нулевую площадку).
![]() .
.
Провод 1–2 перерезает
поток ( ![]() ),
но движется против сил действия магнитного
поля.
),
но движется против сил действия магнитного
поля.
![]() .
.
Тогда общая работа по перемещению контура
![]() или
или
|
|
|
(2.9.2) |
|
здесь ![]() –
этоизменение магнитного потока,
сцепленного с контуром.
–
этоизменение магнитного потока,
сцепленного с контуром.
Работа, совершаемая при перемещении замкнутого контура с током в магнитном поле, равна произведению величины тока на изменение магнитного потока, сцепленного с этим контуром.
Элементарную работу по бесконечно малому перемещению контура в магнитном поле можно найти по формуле
|
|
|
(2.9.5) |
|
Выражения (2.9.1) и (2.9.5) внешне тождественны, но физический смыслвеличины dФразличен.
Соотношение (2.9.5),
выведенное нами для простейшего случая,
остаётся справедливым для контура любой
формы в произвольном магнитном поле.
Более того, если контур неподвижен, а
меняется ![]() ,
то при изменении магнитного потока в
контуре на величину dФ, магнитное поле
совершает ту же работу
,
то при изменении магнитного потока в
контуре на величину dФ, магнитное поле
совершает ту же работу![]()
