2. Сила Лоренца

Сила Лоренца—сила, с которой, в рамкахклассической физики,электромагнитное поледействует наточечнуюзаряженнуючастицу. Силой Лоренца называют иногда силу, действующую на движущийся со скоростьюзарядлишь со сторонымагнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще^[1]иначе говоря, со стороныэлектрическогоимагнитногополей в системеСИ:

Названа в честь голландского физикаХендрика Лоренца, который вывел выражение для этой силы в 1892 году. За три года до Лоренца правильное выражение было найденоХевисайдом^[2].

Частным случаем силы Лоренца является сила Ампера.

F_Л= q υ B sin α.

3. Закон Ампера

Зако́н Ампе́ра— закон взаимодействия постоянныхтоков. УстановленАндре Мари Амперомв1820. Из закона Ампера следует, что параллельныепроводникис постоянными токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются. Законом Ампера называется также закон, определяющий силу, с котороймагнитное поледействует на малый отрезок проводника с током. Сила, с которой магнитное поле действует на элемент объёмаdVпроводника с током плотности, находящегося в магнитном поле с индукцией:

.

Если ток течёт по тонкому проводнику, то , где— «элемент длины» проводника — вектор, по модулю равныйdlи совпадающий по направлению с током. Тогда предыдущее равенство можно переписать следующим образом:

Направление силы определяется по правилу вычислениявекторного произведения, которое удобно запомнить при помощиправила левой руки.

Модуль силы Ампера можно найти по формуле:

,

где α — угол между векторами магнитной индукции и тока.

Сила dFмаксимальна когда элемент проводника с током расположен перпендикулярно линиям магнитной индукции ():

.

dF = I*B*dlsina

4. Теорема Гаусса для магнитного поля в вакууме (инт. И дифф. Вид)

Теорема Гаусса— основная теоремаэлектродинамики, которая применяется для вычисления электрических полей, входит в системууравнений Максвелла. Она выражает связь между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченном этой поверхностью.

Общая формулировка:Поток векторанапряжённости электрического полячерез любую, произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхностиэлектрическому заряду.

где

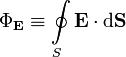• — поток вектора напряжённости электрического поля через замкнутую поверхностьS.

• Q— полный заряд, содержащийся в объёме, который ограничивает поверхностьS.

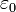• —электрическая постоянная.

Данное выражение представляет собой теорему Гаусса в интегральной форме.

В дифференциальной форме теорема Гаусса выражается следующим образом:

Здесь ρ — объёмная плотность заряда (в случае присутствия среды — суммарная плотность свободных и связанных зарядов), а —оператор набла.

Для теоремы Гаусса справедлив принцип суперпозиции, то есть поток вектора напряжённости через поверхность не зависит от распределения заряда внутри поверхности.

Физической основой теоремы Гаусса является закон Кулонаили, иначе, теорема Гаусса является интегральной формулировкойзакона Кулона.

5. Теорема о циркуляции для магнитного поля в вакууме (инт. И дифф. Вид)

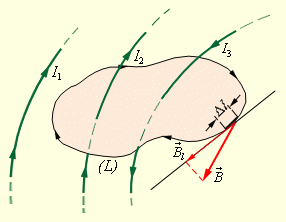
Поясним понятие циркуляциивектораПусть в пространстве, где создано магнитное поле, выбран некоторый условный замкнутый контур (не обязательно плоский) и указано положительное направление его обхода. На каждом отдельном малом участке Δlэтого контура можно определить касательную составляющуювекторав данном месте, то есть определить проекцию векторана направление касательной к данному участку контура (рис. 1.17.2).

Рисунок 1.17.2. Замкнутый контур (L) с заданным направлением обхода. Изображены токиI1,I2иI3, создающие магнитное поле

Циркуляцией вектора называют сумму произведенийΔl, взятую по всему контуруL:

Некоторые токи, создающие магнитное поле, могут пронизывать выбранный контур Lв то время, как другие токи могут находиться в стороне от контура.

Теоремаоциркуляцииутверждает, что циркуляция векторамагнитногополяпостоянных токов по любому контуруLвсегда равна произведению магнитной постоянной μ₀на сумму всех токов, пронизывающих контур:

В качестве примера на рис. 1.17.2 изображены несколько проводников с токами, создающими магнитное поле. Токи I₂иI₃пронизывают контурLв противоположных направлениях, им должны быть приписаны разные знаки – положительными считаются токи, которые связаны с выбранным направлением обхода контура правилом правого винта (буравчика). Следовательно,I₃> 0, аI₂< 0. ТокI₁не пронизывает контурL.

Теоремаоциркуляциив данном примере выражается соотношением:

Теоремаоциркуляциив общем виде следует из закона Био–Савара и принципа суперпозиции.

Простейшим примером применения теоремы о циркуляцииявляется вывод формулы для магнитной индукцииполяпрямолинейного проводника с током. Учитывая симметрию в данной задаче, контурLцелесообразно выбрать в виде окружности некоторого радиусаR, лежащей в перпендикулярной проводнику плоскости. Центр окружности находится в некоторой точке проводника. В силу симметрии векторнаправлен по касательной, а его модуль одинаков во всех точках окружности. Применение теоремы оциркуляцииприводит к соотношению:

откуда следует формула для модуля магнитной индукции поляпрямолинейного проводника с током, приведенная ранее.

Этот пример показывает, что теоремаоциркуляциивектора магнитной индукцииможет быть использована для расчета магнитных полей, создаваемых симметричным распределением токов, когда из соображений симметрии можно «угадать» общую структуруполя.

Имеется немало практически важных примеров расчета магнитных полей с помощью теоремы о циркуляции. Одним из таких примеров является задача вычисленияполятороидальной катушки