4. Линии магнитной индукции

Линии магнитной индукции- линии, касательные к которым направлены также как ивектормагнитной индукции в данной точке пМагнитные поля, так же как и электрические, можно изображать графически при помощи линий магнитной индукции. Через каждую точку магнитного поля можно провести линию индукции. Так как индукция поля в любой точке имеет определённое направление, то и направление линии индукции в каждой точке данного поля может быть только единственным, а значит, линии магнитного поля, так же как и электрического поля, линии индукции магнитного поля прочерчивают с такой густотой, чтобы число линий, пересекающих единицу поверхности, перпендикулярной к ним, было равно (или пропорционально) индукции магнитного поля в данном месте. Поэтому, изображая линии индукции, можно наглядно представить, как меняется в пространствеиндукция, а следовательно, инапряжённость магнитного поляпо модулю и направлению.

5. Магнитное поле прямого тока

Применим закон Био–Савара–Лапласа для расчета магнитных полей простейших токов.

      Рассмотрим магнитное поле прямого тока (рис. 1.6).

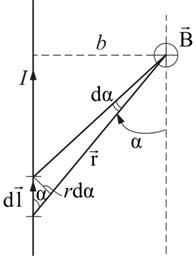
Рис. 1.6

      Все векторы от произвольных элементарных участковимеют одинаковое направление. Поэтому сложение векторов можно заменить сложением модулей.

      Пусть точка, в которой определяется магнитное поле, находится на расстоянии bот провода. Из рисунка 1.6 видно, что:

      Подставив найденные значения rи dlв закон Био–Савара–Лапласа, получим:

      Для конечного проводникаугол α изменяется от , до. Тогда

,

(1.5.1)

      Для бесконечно длинного проводникаа, тогда

      или, что удобнее для расчетов,

,

(1.5.2)

      Линии магнитной индукции прямого тока представляют собой систему концентрических окружностей, охватывающих ток (рис. 1.3).

6. Магнитная индукция в центре кругового тока

Рассмотрим поле, создаваемое током I, текущим по тонкому проводу, имеющему форму окружности радиусаR(рис. 1.7).

Рис. 1.7

      Определим магнитную индукцию на оси проводника с током на расстоянии хот плоскости кругового тока. Векторыперпендикулярны плоскостям, проходящим через соответствующиеи. Следовательно, они образуют симметричный конический веер. Из соображения симметрии видно, что результирующий векторнаправлен вдоль оси кругового тока. Каждый из вектороввносит вклад равный, авзаимно уничтожаются. Но,, а т.к. угол междуиα – прямой, тотогда получим

,

(1.6.1)

      Подставив в (1.6.1) и, проинтегрировав по всему контуру, получим выражение для нахождениямагнитной индукции круговоготока:

,

(1.6.2)

При , получиммагнитную индукцию в центре кругового тока:

,

(1.6.3)

      Заметим, что в числителе (1.6.2)   – магнитный момент контура. Тогда, на большом расстоянии от контура, при, магнитную индукцию можно рассчитать по формуле:

,

(1.6.4)

      Силовые линии магнитного поля кругового тока хорошо видны в опыте с железными опилками (рис. 1.8).

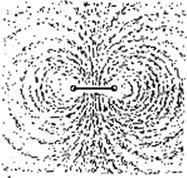
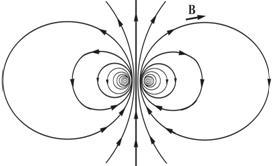
Рис. 1.8

7. Дипольный магнитный момент

Магни́тный моме́нт, магни́тный дипо́льный моме́нт — основная величина, характеризующая магнитные свойства вещества. Источником магнетизма, согласно классической теории электромагнитных явлений, являются электрические макро- и микротоки. Элементарным источником магнетизма считают замкнутый ток. Магнитным моментом обладают элементарные частицы, атомные ядра, электронные оболочки атомов имолекул. Магнитный момент элементарных частиц (электронов, протонов, нейтронов и других), как показала квантовая механика, обусловлен существованием у них собственного механического момента — спина.

Магнитный момент измеряется в А⋅м² или Дж/Тл (СИ).
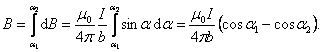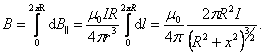