37. Индуктивность
Индукти́вность— коэффициент пропорциональности междумагнитным потоком(создаваемымтокомкакого-либо витка при отсутствиинамагничивающих сред, например, в воздухе) ивеличинойэтого тока[1][2][3].
Если в проводящем контуре течёт ток, то ток создаёт магнитное поле[3]. Величинамагнитного потока, пронизывающего одновитковый контур, связана с величиной тока следующим образом[3]:
где L— индуктивность витка. В случаекатушки, состоящей из N витков предыдущее выражение модифицируется к виду:
где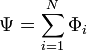 
—
сумма магнитных потоков через все витки,
аL— уже индуктивность
многовитковой катушки. Ψ называютпотокосцеплениемили
полным магнитным потоком[4].
Коэффициент пропорциональностиLиначе
называетсякоэффициентом
самоиндукцииконтура или просто
индуктивностью[3].
Если поток, пронизывающий каждый из витков одинаков, то Ψ = NΦ. Соответственно,LN=L1N2(суммарный магнитный поток увеличивается в N раз и потокосцепление еще в N раз). Но в реальных катушках магнитные поля в центре и на краях отличаются, поэтому используются более сложные формулы.
В системе единиц СИиндуктивность измеряется вгенри[5], сокращенно Гн, в системеСГС— в сантиметрах (1 Гн = 109см)[3]. Контур обладает индуктивностью в один генри, если при изменении тока на одинамперв секунду на выводах контура будет возникать напряжение в одинвольт. Реальный, не сверхпроводящий, контур обладает омическим сопротивлением R, поэтому на нём будет дополнительно возникать напряжение U=I*R, где I —сила тока, протекающего по контуру в данное мгновение времени.
Символ L, используемый для обозначения индуктивности, был взят в честьЛенца Эмилия Христиановича(Heinrich Friedrich Emil Lenz)[источник не указан 447 дней]. Единица измерения индуктивности названа в честьДжозефа Генри(Joseph Henry)[6]. Сам термин индуктивность был предложенОливером Хевисайдом(Oliver Heaviside) в феврале1886 года[источник не указан 447 дней].
Через индуктивность выражается ЭДС самоиндукциив контуре, возникающая при изменении в нём тока[3]:
.
При заданной силе тока индуктивность определяет энергиюмагнитного поля тока[3]:
.
Практически участки цепи со значительной индуктивностью выполняют в виде катушек индуктивности[3].
38. Энергия магнитного поля проводника с током
Магни́тное по́ле —
составляющая электромагнитного
поля,
появляющаяся при наличии изменяющегося
во времени электрического
поля.
Кроме того, магнитное поле может
создаваться током
заряженных частиц,
либо магнитными
моментами электронов в атомах (постоянные
магниты).
С точки зрения квантовой теории
поля электромагнитное
взаимодействие переносится
безмассовым бозон-фотоном (частицей,
которую можно представить как квантовое
возбуждение электромагнитного поля).
Основной характеристикой магнитного
поля является его сила, определяемая
вектором магнитной
индукции 
(вектор
индукции магнитного поля)[1].
В СИ магнитная индукция измеряется
в теслах (Тл),
в системе СГС в гауссах.
Магнитное поле — это особый вид материи, посредством которой осуществляется взаимодействие между движущимися заряженными частицами или телами, обладающими магнитным моментом.
Можно также рассматривать магнитное поле, как релятивистскую составляющую электрического поля. Точнее, магнитные поля являются необходимым следствием существования электрических полей испециальной теории относительности. Вместе, магнитное и электрическое поля образуют электромагнитное поле, проявлениями которого являются свет и прочие электромагнитные волны.
Энергия магнитного поля
Приращение плотности энергии магнитного поля равно:
где:
—напряжённость
магнитного поля,
—магнитная
индукция
В линейном тензорном приближении (Bi= μ0μijHj) плотность энергии равна:
где:
μij—тензормагнитной проницаемости,
μii— диагональные компоненты этого тензора,
μ0—магнитная постоянная
В изотропном линейном магнетике:
где:
μ — относительная магнитная проницаемость
В вакууме μ = 1 и:
Энергию магнитного поля в катушке индуктивности можно найти по формуле:
где:
Φ — магнитный поток,
I— ток,
L—индуктивностькатушки или витка с током.