Лекции по высшей математике / 16-19

16. Если в точке zD существует предел 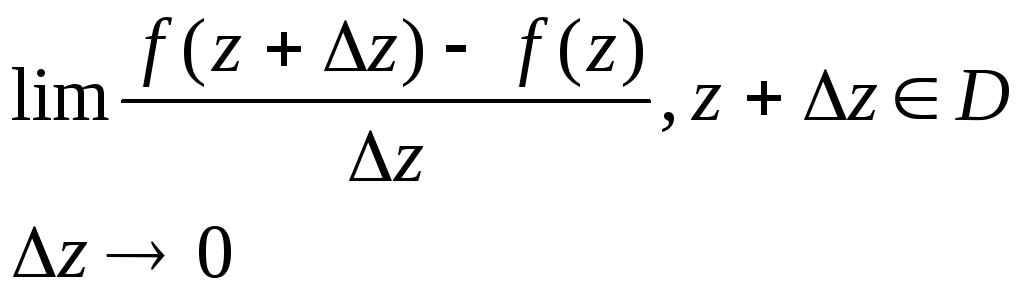, то он называется производной функции f(z) в точке z и обозначается через f^э(z) или . Если в точке zD функция f(z) имеет производную f^э(z), то говорим, что функция f(z) дифференцируема в т. z. Ф-ция f(z), дифференцируемая в каждой точке области D и имеющая в этой области непрерывную производную f^э(z), называется аналитической в области D. Будем также говорить, что f (z) аналитическая в точке z₀D, если f (z) является аналитической в некоторой окрестности точки z₀.

Для того чтобы функция f (z) = и (х,y)+iv (х, у) была аналити­ческой в области D, необходимо и достаточно существование в этой области непрерывных частных производных функций и (х, у) и v (х, у), удовлетворяющих условиям Коши — Римана или, в полярных координатах,

При. выполнений условий или производная f'(z) может быть записана соответственно:.Формулы дифференцирования функций комплексной переменной аналогичны соответствующим формулам дифференцирования функций действительной переменной.

Пример 1. Доказать, что функция f(z)—e^2z аналитична и найтиf'.(z). Имеем e^2z=e^2x(cos2y+isin2y), т.е.и(х,у) = е^2x cos 2y, v (х, у)=е^2x sin 2y.Поэтому

= 2е^2xсоs2y, = — 2e^2x sin 2y,

=2e^2xsin2у,=2e^2xcos2y.

Следовательно, условия (1) выполняются во всей плоскости, и по первой из формул (e^2z )’=2e^2x cos2y+i2e^2x sin2y=2e^2x(cos2y+isin2y)=2e^2z. Ряд свойств, характерных для диф. ф-ций действительной переменной сохраняется и для аналитических функций. Заданием действительной или мнимой части аналитическая в области D функция определяется с точностью до комплексной постоянной. Например если u(x,y) – действительная часть аналитической ф-ции f(z), то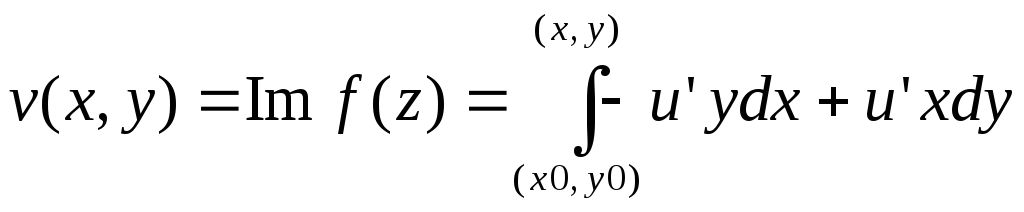 , где (x₀ ,y_o) – фиксированная точка в области D и путь интегрирования также лежит в области D.

17. Понятие ф-ции компл. переменной. Множество точек Е расширенной комплексной плоскости (z)= называется связным, если любые две его точки можно соединить непрерывной кривой, все точки которой принадлежат данному множеству. Связное открытое множество точек комплексной плоскости называется областью и обозначается через D,G и т.п. Область D наз-ется односвязной, если ее граница является связным множеством: в противном случае область D наз-тся многосвязной. Если каждому комплексному числу z. принадлежащему области D, поставлено в соответствие нек. комплекс. число w, то говорят, что в области D определена компл. ф-ция w=f(z). Пусть zx+iy и w=u+iv. Тогда w=f(z) может быть представлена с помощью двух действительных ф-ций u=u(x,y), v=v(x,y) действительных переменных x, y: w=f(z)=u+iv=u(x,y)+iv(x,y), u(x,y)=Ref(z), v(x,y)=Imf(z). Пример:Найти действ. и мнимую части функции f(z)=iz²-. Полагая z=x+iy, f(z)=u(x,y)+iv(x,y)=i(x+iy)²-(x-iy)=i(x²-y²+2ixy)-(x-iy)=-x(1+2y)+i(x²-y²+y). Ref(z)=u(x,y)=-x(1+2y), Imf(z)=v(x,y)=x²-y²+y.

Интеграл. Пусть l – дуга направленной кусочно гладкой кривой в плоскости (z), точки z_kl, k=0,1…n, разбивают дугу l на частичные дуги, на каждой из которых выбрано по одной точке ξ_к, к=1…n. По определению полагаем, при условии. что предел в правой части существует и не зависит ни от способа разбиения дуги l, ни от выбора точек ξ. Если ф-ция f(z) непрерывна на l, то интеграл существует. Пример: Вычислить , где l – радиус вектор точки 1+i. Разбиваем радиус вектор точки 1+i на n равных частей, т.е. полагаем z_k=k/n+ik/n, z_k=1/n(1+i), k=0,1…n, ξ_k=z_k. Тогда Следовательно

18. Ряды с комплексными членами

Рассмотрим последовательность комплексных чисел z₁, z₂… z_n, ..., где z_n=a_n+ib_n (n=1, 2, ...).

Определение 1. Комплексное число z₀ = а+ib называется пределом последовательности комплексных чисел z_n=a_n+ib_n, eсли

lim|z_n—z₀|=О.(1) Напишем условие (1) в развернутом виде:

z_n-z₀=(a_n-ib_n)-(a+ib)=(a_n-a)+i(b_n-b)

На основании равенства следует, что условие (1) будет выполняться только тогда, когда будут выполняться условия

lima_n=a, limb_n=b Составиm ряд из комплексных чисел w₁+w₂ …w_n где w_n=u_n+iv_n n=(1,2…). Рассмотрим сумму n членов ряда. которую обозначим через s_n:

s_n= w₁+w₂ …w_n. s_{n –} есть комплексное число. s_n=.

Определение 2. Если существует предел lims_n=s=A+iB

то ряд называется сходящимся рядом и s называется его суммой:

s==A+iB. На основании равенств из условия следуют равенства

A= lim B=

Если не существует lims_n то ряд называется расходящимся.

Для исследования сходимости ряда эффективной является следующая теорема. ' - . *

Теорема 1. Если сходится ряд, составленный из модулей членов ряда, , где w_n =

Доказательство. Из сходимости ряда и условий = w_n следуют равенства (на основании соответствующей теоремы об абсолютной сходимости рядов с действительными членами), а следовательно, равенство.

Доказанная теорема позволяет применять для исследования сходимости рядов с комплексными членами все достаточные при сходимости рядов с положительными членами.

Определение. Ряд называется абсолютно сходящимся, если сходится ряд, составленный из модулей его членов,

Приведем без доказательства следующую теорему.

Теорема 1 . Область сходимости степенного ряда с комплекс­ными членами есть круг на плоскости комплексной перемен­ной z с центром в начале координат. Его называют кругом схо­димости. В точках лежащих внутри круга сходимости, ряд сходится абсолютно.

Радиус круга сходимости R называют радиусом сходимости степенного ряда. Если R — радиус сходимости степенного ряда, то пишут, что ряд сходится в области.

Ряд Тэйлора: для ф-ции f(x) в окрестности точки х=а справедлива фор-ла Тэйлора f(x)=(x-a)/1*f’(a)+(x-a)²/2!*f’’(a)+…+(x-a)ⁿ/n!*f⁽ⁿ⁾(a)+R_n(x), R_n=(x-a)ⁿ⁺¹/(n+1)!*f⁽ⁿ⁺¹⁾*(a+H(x-a)), 0<H<1. При

f(x)=(x-a)/1*f’(a)+(x-a)²/2!*f’’(a)+…+(x-a)ⁿ/n!*f⁽ⁿ⁾(a) при limR_n(x)=0

Ряд Лорана:При этом ряд является главной частью, а ряд- правильной частью.

Теорема Лорана: Если ф-ция f(z) аналитична в кольце 0<=r<(z-z₀)<R, то в этом кольце она единственным образом представима в виде ряда Лорана.Для ф-ции f(z) в окрестности точки z=∞:сходящийся в кольце r<(z)<+∞

Пример. Разложить в ряд Лорана по степеням z f(z)=1/z(1-z).Область сходимости – кольцо 0<r<1. , для т=-2,-3. Применяя ф-лу Коши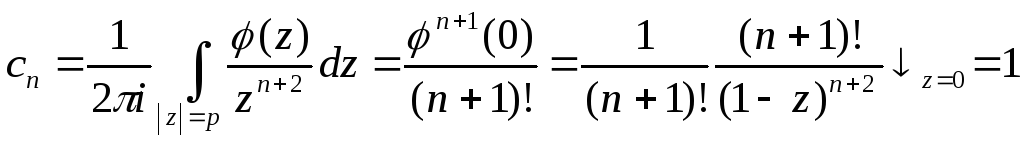Так для 0<z<1 f(z)=1/z(1-z)=1/z+1/(1-z)

19. Понятие ф-ции компл. переменной. Множество точек Е расширенной комплексной плоскости (z)= называется связным, если любые две его точки можно соединить непрерывной кривой, все точки которой принадлежат данному множеству. Связное открытое множество точек комплексной плоскости называется областью и обозначается через D,G и т.п. Область D наз-ется односвязной, если ее граница является связным множеством: в противном случае область D наз-тся многосвязной. Если каждому комплексному числу z. принадлежащему области D, поставлено в соответствие нек. комплекс. число w, то говорят, что в области D определена компл. ф-ция w=f(z). Пусть zx+iy и w=u+iv. Тогда w=f(z) может быть представлена с помощью двух действительных ф-ций u=u(x,y), v=v(x,y) действительных переменных x, y: w=f(z)=u+iv=u(x,y)+iv(x,y), u(x,y)=Ref(z), v(x,y)=Imf(z). Пример:Найти действ. и мнимую части функции f(z)=iz²-. Полагая z=x+iy, f(z)=u(x,y)+iv(x,y)=i(x+iy)²-(x-iy)=i(x²-y²+2ixy)-(x-iy)=-x(1+2y)+i(x²-y²+y). Ref(z)=u(x,y)=-x(1+2y), Imf(z)=v(x,y)=x²-y²+y.

Нули: ???