3.2. Динамика поступательного и вращательного движения План решения задач с помощью законов динамики

1. Поступательное движение тел.

1) Выделите систему взаимодействующих тел. Сделайте рисунок.

2) Укажите на рисунке силы, действующие на каждое тело. Учтите, что силу трения можно показать, если известно направление движения.

 3) Выберите систему координат. Удобно для каждого тела одну из координатных осей направить по направлению ускорения тела.

4) Запишите для каждого тела закон динамики движения – 2-й закон Ньютона, в следующем виде:

.

5) Запишите этот закон в проекциях на координатные оси и выразите определяемую величину.

6) По полученной расчетной формуле произведите вычисления.

2. Вращательное движение тел.

1) Запишите закон динамика вращательного движения тела относительно неподвижной оси вращения.

2) Покажите на рисунке плечо силы и расстояния масс от оси вращения, необходимые для расчета момента инерции тела. Запишите определительные формулы для момента силы M и момента инерции I; при этом обратите внимание на то, чтобы величины M и I , были записаны относительно одной и той же оси вращения тела.

3) Из закона динамики получите расчетную формулу определяемой величины и произведите вычисления.

Задача 4. Мяч массой упруго ударяется о стену под углом к нормали. Определите величину и направление импульса силы, который действовал на стенку во время удара. Скорость мяча .

Дано Решение

; При упругом ударе величина скорости не изменяется

; ( ) и угол, под которым отскакивает мяч, равен углу

. падения мяча (рис. 4). Мяч в условии задачи можно

принять за материальную точку, пренебрегая его размерами,

а стену рассматривать как абсолютно твердое тело.

При взаимодействии мяча со стеной на мяч действует Земля: силой тяжести, – и стена: силой упругости . Однако проекция силы тяжести на ось равна нулю; поэтому величину силы тяжести мяча можно исключить из дальнейшего рассмотрения. Под действием силы упругости изменяется направление скорости мяча.

Запишем второй закон Ньютона в виде: (1) где – средняя сила, с которой стена действует на мяч; – время взаимодействия мяча со стеной. Для того, чтобы уравнение (1) переписать в скалярном виде, нужно знать направление силы . Из уравнения (1) следует, что импульс силы удара мяча совпадает по направлению с вектором приращения импульса мяча , т. е.

По правилу вычитания векторов

найдем вектор приращения импульса

мяча , он направлен

перпендикулярно поверхности стены.

Следовательно, и импульс силы ,

действующий на мяч, направлен вдоль

нормали к поверхности стены.

Перепишем уравнение (1) в

проекции на ось x:

.

Так как , то

Рис. 4

(2)

Нас интересует импульс силы, действующий на стену во время удара. Используем третий закон Ньютона: сила 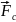, с которой мяч действует на стену, равна по величине и противоположно направлена силе , с которой стена действует на мяч (см. рис. 4):

Отсюда, с учетом формулы (2), получаем .

Вычислим импульс силы:

Задача 5. Маховик в виде диска радиусом и массой был раскручен до частоты вращения , а затем был предоставлен самому себе. Под действием сил трения маховик остановился через . Определите момент сил трения.

Дано Решение

; В соответствии с основным законом динамики

; вращательного движения момент сил трения равен

; скорости изменения момента импульса маховика:

; . (1)

. По условию задачи маховик представляет собой твердый сплошной диск, момент инерции которого

относительно его оси симметрии

(2)

С учетом формулы (2) из закона динамики (1) получаем момент сил трения

, (3)

где – угловое ускорение маховика.

Так как угловое ускорение и момент сил трения в данном случае сонаправлены, то векторное уравнение (3) можно заменить скалярным:

(4)

При равнозамедленном вращении (вектор (рис. 5)) величина углового ускорения определяется выражением

(5)

З десь конечная угловая скорость , а начальная . Подставив ускорение в закон динамики (4), получаем величину момента силы

(6)

Проверим расчетную формулу (6) по единицам измерения. Подстановка единиц измерения величин в правую часть этого равенства:

, –

дает единицу определяемой физической величины – момента сил.

Вычисляем момент силы трения по формуле (6):

.

Задача 6. Блок, имеющий форму диска массой , укреплен на краю горизонтального стола. Гири массой и соединены невесомой нитью, перекинутой через блок (рис. 6). Коэффициент трения гири о поверхность стола Определите ускорение , с которым движутся гири, и силы натяжения нити и по обе стороны блока. Трением при вращении блока можно пренебречь.