2

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ЛИПЕЦКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ

Лабораторная работа №1

по дисциплине

«Математический анализ»

на тему:

«Вычисление интеграла методом трех восьмых»

Студент

подпись, дата

фамилия, инициалы

Группа

Принял

Ермолаев Ю.Д.

ученая степень, звание

подпись, дата

фамилия, инициалы

Липецк 2010

1. Задание

Вычислить интеграл методом трех восьмых:

Вариант 21:

2. Краткие теоретические сведения

Правило трех восьмых

, где . (*)

Остаточный член имеет вид .

Заметим, что в правиле трех восьмых число узлов обязательно равно 3m + 1, то есть n = 3m.

Если функция y = f(x) задана таблично и ее производные найти затруднительно, то в предположении отсутствия быстроколеблющихся составляющих можно применять приближенные формулы для погрешностей, выраженные через конечные разности:

, где под подразумевается среднее арифметическое значение разностей соответствующего порядка.

3. Листинг программы

#include <stdio.h>

#include <conio.h>

#include <stdlib.h>

#include <locale.h>

#include <math.h>

double f(double x)

{

double y;

y=cos(x)/(x+1.0);

return y;

}

double method(int n)

{

double x,h,s=0,a,b,s1=0,s2=0,s3=0;

int m;

a=0;

b=(3.141592653589793238462643383/2.0);

m=n*3-1;

h=(b-a)/(3*n);

s1=f(a)+f(b);

for(int i=1;i<=m;i++)

{

x=a+h*i;

if(i%3==0)

s3=s3+f(x);

else

s2=s2+f(x);

}

s=3.0/8.0*(s1+3*s2+2*s3)*h;

return s;

}

void main()

{

double s=0,res;

int n,m;

setlocale(LC_ALL,"Rus");

for(m=3,n=1;m<13 || abs(method(m-1)-method(m))/15.0>0.0001;m*=2,n++)

printf("\n%d Количество отрезков:%d\nИнтеграл = %.15lf\nПогрешность: %e\n",n,3*m,method(m),abs(method(m-1)-method(m))/15.0);

res=method(m/4.0)+(pow(method(m/4.0)- method(m/2.0),2.0)/(method(m/4)-2*method(m/2.0)+method(m)));

printf("\nИнтеграл посчитан: %e",res);

getch();

}

Вычисляются минимум 3 прохода (9,18,36 отрезков). Затем, если требуется вычисление продолжается.

Далее итоговое значение интеграла рассчитывается в соответствие с процессом Эйткена:

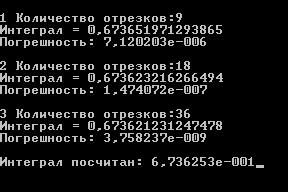
4. Контрольный пример

Проход	Количество отрезков	Значение интеграла	Погрешность
1	9	0,673651971293865	7,12 * 10^-6
2	18	0,673623216266494	1.47 * 10^-7
3	36	0,673621231247478	3.75 * 10^-9

Согласно процессу Эйткена

I=0,67362537

Ответ: 0,67362537± 0.00000001