
- •3. Методы анализа и синтеза управления.
- •3.1. Методы анализа управления (Лекция 10)
- •3.1.1. Управляемость, наблюдаемость.
- •3.1.1.1. Управляемость: определение (Пример 3.1)
- •3.1.1.2. Наблюдаемость: определение (Пример 3.2)
- •3.1.2. Корневой годограф
- •3.1.2.1. Определение корневого годографа
- •3.1.2.2. Свойства корневого годографа
- •3.1.2.3. Пример построения корневого годографа (Пример 3.3)
- •3.2. Управление и стабилизация (Лекция 11)
- •3.2.1. Цель управления, идеальное управление
- •3.2.1.1. Общая схема разомкнутого и замкнутого управления
- •3.2.1.2. Идеальное управление
- •3.2.1.3. Пример определения идеального управления (Пример 3.4)
- •3.2.1.4. Невозможность реализации идеального управления
- •3.2.1.5. Иллюстрация недостатков идеального управления (Пример 3.5)
- •3.3. Стабилизация с помощью обратной связи (Лекция 12)
- •3.3.1. Введение обратной связи
- •3.3.1.1. Определение обратной связи в скалярном случае
- •3.3.1.2. Иллюстрация определения стабилизирующей обратной связи (Пример 3.6)
- •3.3.2. Общий алгоритм стабилизации
- •3.3.2.1. Общий вид обратной связи
- •3.3.2.2. Замкнутое представление объекта и обратной связи
- •3.3.2.3. Алгоритм выбора стабилизирующей обратной связи в общем случае
- •3.3.3. Некоторые другие законы управления
- •3.3.3.1. Программное управление в комбинации с обратной связью по выходу
- •3.3.3.2. Управление по возмущению
- •3.3.3.3. Управление с обратной связью по ошибке
- •3.4. Удовлетворение некоторых требований к качеству управления (Лекция 13)
- •3.4.1. Некоторые характеристики качества управления
- •3.4.1.1. Переходный процесс детерминированной системы и его некоторые характеристики
- •3.4.1.2. Некоторые требования к переходному процессу и установившейся ошибке
- •3.4.2. Методика удовлетворения требований к качеству
- •3.4.2.1. Теорема о реакции на полиномиальное воздействие
- •3.4.2.2. Обеспечение требования ограниченности установившейся ошибки
- •3.4.2.3. Обеспечение ограниченности амплитуды ошибки при периодическом воздействии
- •3.4.2.4. Обеспечение ограниченности амплитуды ошибки при периодической помехе
3.4. Удовлетворение некоторых требований к качеству управления (Лекция 13)
3.4.1. Некоторые характеристики качества управления
3.4.1.1. Переходный процесс детерминированной системы и его некоторые характеристики
Подбор закона регулирования направлен на придание желательного вида переходным процессам в системе, его длительности, значению установившихся ошибок и другим характеристикам функционирования объекта при работе регулятора в замкнутом режиме.
По величине установившегося значения ошибки (уклонения текущего значения выходной величины от заданного, эталонного значения) системы делятся на статические и астатические. Система называется астатической, если установившееся значение ошибки равно нулю. Если же установившееся значение ошибки не равно нулю, то система называется статической.
Чтобы система являлась статической по отношению к воздействию необходимо, чтобы её передаточная функция по данному воздействию (каналу) при pобращалась в постоянную величину, а чтобы система была астатической необходимо, чтобы передаточная функция при р=0 имела нуль какого-либо порядка, этот порядок называется порядком астатизма системы.
Используются различные характеристики качества управления и функционирования системы. Некоторые из них показаны на рис. 3.5:
xm- максимальное отклонение регулируемой переменной;
m- значение максимума перерегулирования в %;
tр- время протекания переходного процесса;
tm- время наступления первого максимума;
(dx/dt)m- максимальная скорость отработки регулируемой переменной.
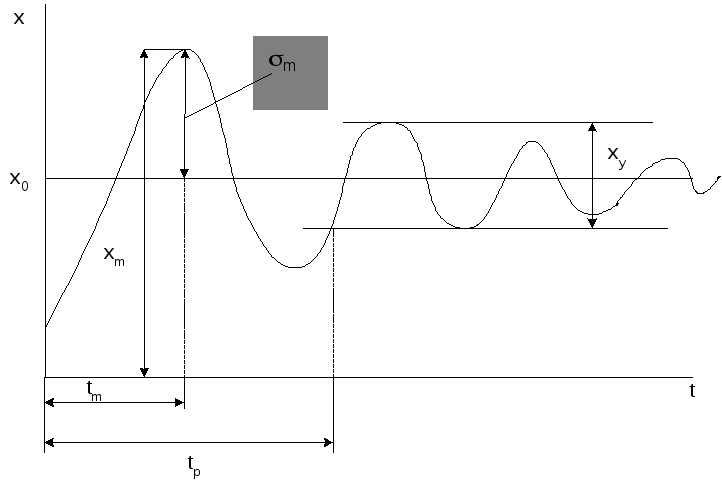
Рис. 3.5. Вид переходного процесса.
3.4.1.2. Некоторые требования к переходному процессу и установившейся ошибке
Часто характеристики и требования связываются с видом воздействия на систему. Используются типовые воздействия или сигналы. В настоящее время используется следующий подход .
1). Система должна быть устойчивой
2). Если сигнал имеет вид возрастающей функции, то установившаяся ошибка должна быть ограниченной и не больше заданной, т.е. если сигнал имеет вид
![]() ,
,
![]() ,
(3.50)
,
(3.50)
то установившаяся ошибка его отработки (t) должна быть
![]() (3.51)
(3.51)
где
![]() - заданные значения.
- заданные значения.
3). Если входное воздействие является периодическим с ограниченной амплитудой, то и ошибка должна быть ограниченной в рабочей полосе частот. Если воздействие имеет вид
![]() ,
,![]() (3.52)
(3.52)
при любых r, то ошибка должна быть
|(t)|r(3.53)
где ar ,r,r- соответственно заданные величины: предельная амплитуда входного сигнала, область рабочих частот, предельно допустимая ошибка.
4). Если помеха имеет вид
N (t) = aN cos t, aN aN (3.54)
при N, то установившаяся ошибка от неё должна быть
| |N, N (3.55)
Требование 1) устойчивости системы является непременным условием её работоспособности. Требования 2) - 4) определяют некоторые важные качественные характеристики.
3.4.2. Методика удовлетворения требований к качеству
3.4.2.1. Теорема о реакции на полиномиальное воздействие
Все требования к системе могут быть обеспечены только вариацией параметров регулятора, который чаще всего является звеном обратной связи. В конечном итоге все характеристики обеспечиваются подбором вида переходного процесса системы под влиянием ненулевых начальных условий, при воздействии на её вход возмущения и управления. Процессы эти зависят от передаточных характеристик, от расположения корней на комплексной плоскости. Требования, предъявляемые к системе противоречивы: например, для сокращения времени отработки управляющего воздействия и повышения точности отработки следует увеличивать коэффициент усиления системы, но это может привести к её низкой устойчивости.
Теперь покажем один из возможных способов удовлетворения этих требований, основанный на использовании типовых воздействий на систему.
Пусть воздействие на систему имеет вид
r(t) = a0 + a1t + ....+ aN tN, t 0 (3.56)
тогда имеет место следующая
Теорема. Установившаяся реакция устойчивого звена на полиномиальное воздействие вида (3.56) также является полиномом, представимым в виде
y (t) = c0 r(t) = c1Dr(t) + ... + cN DN r(t) (3.57)
где ck = 1 / k! [dk H(p) / dpk] p=0 , k = 0, 1, ..., N . (3.58)
Отсюда: а) если r(t) = a0, t0, то установившаяся реакция устойчивого звена также постоянная величина, равная:
y(t) =H(0)a0;
б) если r(t) = a0 + a1t , t0, то установившаяся реакция устойчивого звена равна
y (t) = H(p) |p=0 (a0 + a1t) + dH(p) / dp |p=0 a1.
