1. Деревья покрытия. Остовы

7. Пусть – связный граф. Деревом покрытия графа называется подграф, который является деревом, и множество вершин которого совпадает с множеством вершин графа .

Заметим, что связный граф может иметь много различных деревьев покрытия. (Пример)

3. Каждый связный граф содержит в себе дерево покрытия.

2. Пусть – связный граф. Если не содержит циклов, то доказывать ничего не надо, ибо – сам по себе – дерево покрытия.

Предположим, что содержит цикл. Удаление любого ребра из цикла дает граф, который еще остается связным. Если новый граф еще содержит цикл, то опять удалим ребро этого цикла. Продолжим процесс до тех пор, пока результирующий граф не будет содержать ни одного цикла. Мы не удалили ни одной вершины из , и связность графа не нарушилась при удалении ребер. итак, – связный и является деревом покрытия .

8. Пусть – несвязный граф. Остовом (или каркасом) графа называется объединение деревьев покрытия всех его компонент связности.

Очевидно, что в каждом графе существует остов: разрушая в каждой компоненте связности циклы, т.е. удаляя лишние ребра, придем к остову.

1. Число ребер произвольного графа , которые необходимо удалить для получения остова, не зависит от последовательности их удаления и равно .

3. Если – граф является одной из компонент связности графа , то для превращения его в остовное дерево нужно удалить 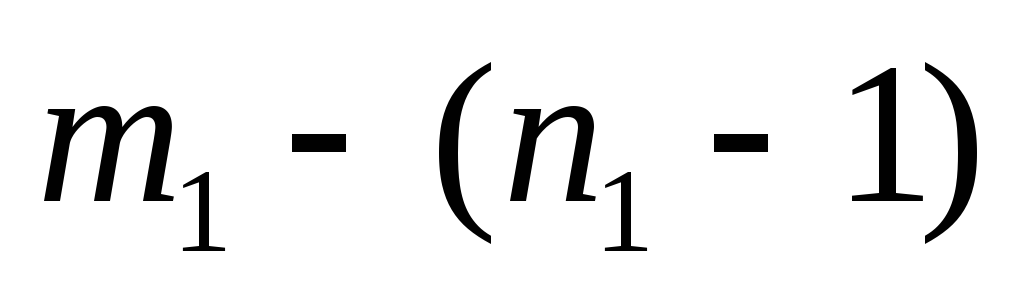подходящих ребер, т.к. в дереве число ребер . Суммируя по всем компонентам, получим требуемое.

9. Число называется цикломатическим числом графа .

6. Раскраска графов

10. Пусть - некоторый граф, натуральное число. Произвольная функция вида называется раскраской графа .

11. Раскраска называется правильной, если любых смежных вершин и

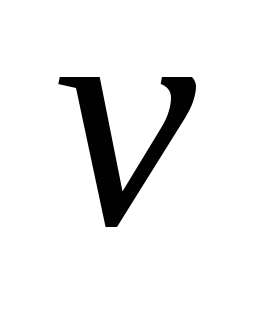
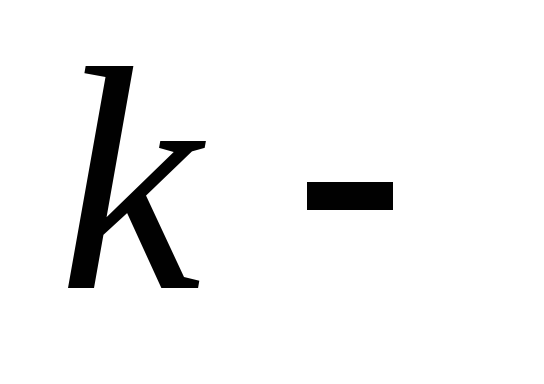12. Граф, для которого правильная раскраска, называется раскрашиваемым (или просто раскрашиваемым цветами).

Правильную раскраску графа можно трактовать как окрашивание каждой его вершины в одни из цветов, при этом смежные вершины должны получить различные цвета.

13. Минимальное число , при котором граф является раскрашиваемым, называется хроматическим числом этого графа и обозначается . Если , то граф называется хроматическим. Правильная раскраска при называется минимальной раскраской.

2. Одна из правильных 4-раскрасок.

Меньшим числом цветов этот граф раскрасить правильно нельзя.

Очевидно, что граф является хроматическим, т.и.т.т., когда он пустой, а хроматическим, когда он двудольный.

Задачи определения хроматического числа и построения минимальной раскраски произвольного графа является очень сложными, эффективные алгоритмы их решения неизвестны.

Рассмотрим простой алгоритм построения правильной раскраски, в ряде случаев приводящий к раскраскам, близким к минимальным.

Алгоритм правильной раскраски

• произвольной вершины графа применим цвет 1.

• Если вершины раскрашены цветами , , то новой произвольно взятой вершине припишем цвет, не использованный при раскраске вершин из её окружения (т.е. инцидентных ей вершин).

Раскраска, к которой приводит данный алгоритм, называется последовательной. Для некоторых графов (напр., для полных двудольных) последовательная раскраска является минимальной. В общем случае это не так.