3. Теория графов

   6. Деревья

      1. Определения

1. Деревом называется связный граф, не содержащий циклов.

2. Любой граф без циклов называется лесом (или ациклическим графом). Таким образом, компонентами леса являются деревья.

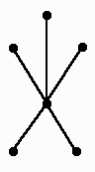
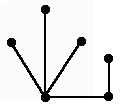
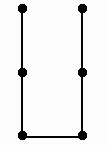
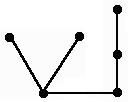
1. На рисунке изображены все деревья с 6 вершинами:

3. Граф, в котором выполняется равенство 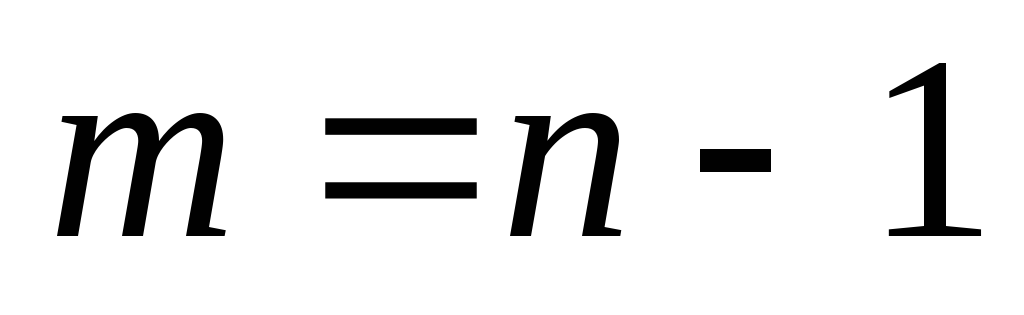, называется древовидным.

4. Пусть - ациклический граф. Если в нем при соединении ребром любой пары несмежных вершин, получится граф ровно с одним простым циклом, то граф будем называть субциклическим.

2. Основные свойства деревьев

Следующая теорема устанавливает, что два из четырех свойств – связность, ацикличность, древовидность и субцикличность – характеризуют граф как дерево.

1. Для 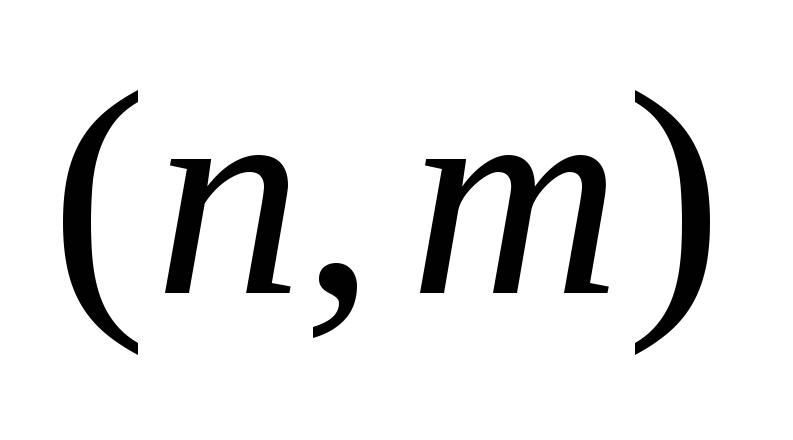– графа следующие утверждения эквивалентны:

   1. – дерево;

   2. Любые две несовпадающие вершины графа соединяет единственная простая цепь;

   3. – связный граф, и любое ребро есть мост;

   4. – связный граф и древовидный;

   5. – ациклический граф (лес) и древовидный;

   6. – ациклический граф (лес) и субцикличекий;

   7. – связный, субциклический и неполный, ;

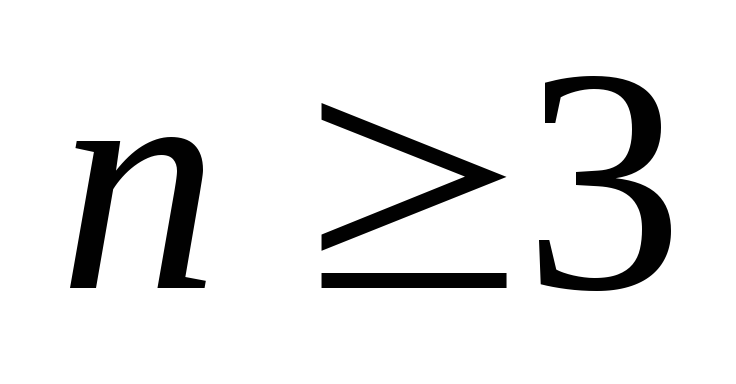   8. – древовидный и субциклический, исключая 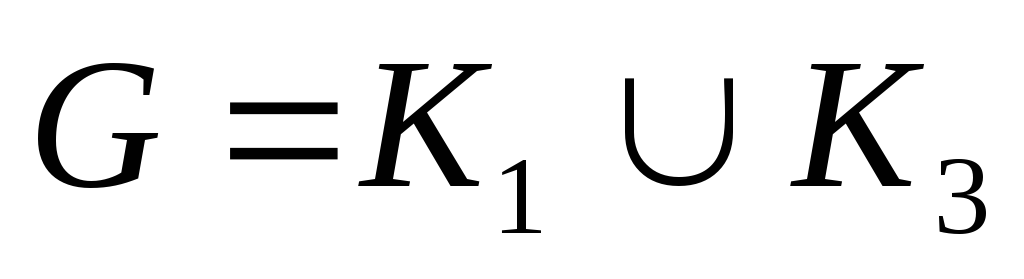и ;

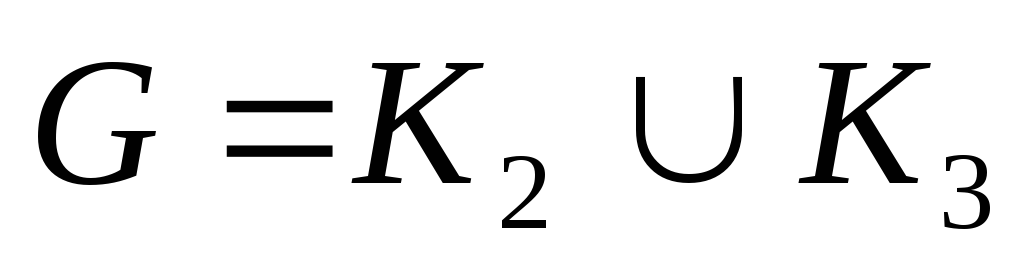(1->2): Если – дерево, то любые две его несовпадающие вершины соединяет единственная простая цепь.

От противного. Пусть существуют две цепи (см. рис.).

Тогда - простой цикл.

(2->3): Если любые две несовпадающие вершины графа соединяет единственная простая цепь, то – связный граф, и любое ребро есть мост.

Имеем: (число компонент связности). Далее от противного. Пусть ребро - не мост. Тогда в концы этого ребра связаны цепью. Само ребро в исходном графе – вторая цепь, что противоречит условию.

(3->4): Если – связный граф, и любое ребро есть мост, то – связный и древовидный ().

Индукция по (числу вершин). Если , то (число ребер). Пусть равенство выполняется для всех графов с числом вершин меньше . Докажем, что оно выполняется и для вершин.

Удалим из ребро , являющееся мостом. Получим две компоненты связности и , для которых верно равенство . Т.е. , . Тогда .

(4->5): Если – связный и древовидный (), то – ациклический граф (лес) и древовидный ().

От противного. Пусть есть цикл с вершинами и ребрами. Остальные вершин связаны с этим циклом ребрами, т.к. граф связный. Следовательно, , что противоречит условию .

Остальное без док-ва.

1. Ориентированные деревья

5. Ориентированным деревом (или ордеревом, или корневым деревом) называется орграф со следующими свойствами:

• существует единственный узел, в который не входит ни один другой узел. Он называется корнем ордерева;

• во все остальные узлы входит только по одному узлу;

• каждый узел достижим из корня.

2. Ордерево обладает следующими свойствами:

1. ;

2. если в ордереве отменить ориентацию ребер, то получится обычное дерево;

3. для каждого узла существует единственный путь, ведущий в этот узел из корня;

4. подграф, определяемый множеством узлов, достижимых из узла , является ордеревом с корнем . Это ордерево называется поддеревом узла .

6. Концевая вершина ордерева называется листом. Путь из корня в лист называется ветвью. Длина наибольшей ветви ордерева называется высотой. Уровень узла ордерева – это расстояние отт корня до узла. Сам корень имеет уровень 0. Узлы одного уровня образуют ярус дерева.