Теория и разбор типовых задач

Добавил:

Valeriya Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Липецкий государственный технический университет

Предмет:

Теория вероятностей и математическая статистика

Файл:

. Отсюда следует, что с возрастанием

.pdf

Скачиваний:

325

Добавлен:

20.06.2014

Размер:

2.24 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 2211 12 13 14 15 16 17 18 19 20 21 22 > Следующая >>>

a 0,

кривой

Выясним, как влияют на форму и расположение нормальной кривой значения параметров а и .

Известно, что графики функций f x и f x a имеют одинаковую форму; сдвинув график f x в положительном направлении оси x на а единиц масштаба при а 0 или в отрицательном направлении при получим график f x a . Отсюда следует, что изменение величины параметра а не изменяет формы нормальной кривой, а приводит лишь к ее сдвигу вдоль оси Оx: вправо, если а возрастает, и влево, если а убывает.

Рассмотрим форму кривой при изменении параметра . Как было указано выше, максимум нормальной кривой

мальная ордината нормальной кривой убывает, а сама кривая становится более пологой, т.е. сжимается к оси Оx; при убывании нормальная кривая становится более «островершинной» и растягивается в положительном направлении оси Оy.

Заметим, что при любых значениях параметров а иплощадь, ограниченная нормальной кривой и осью x, остается равной единице (третье свойство плотности распределения).

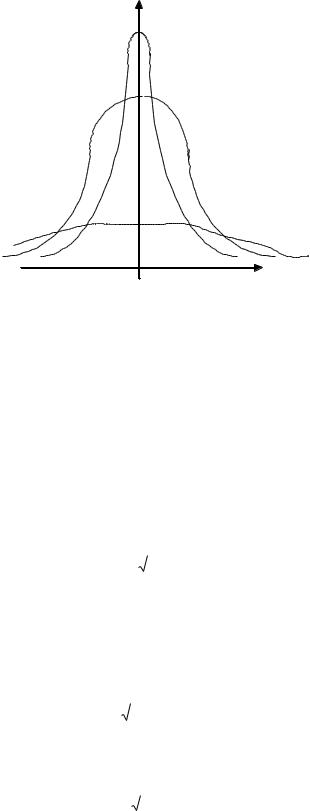
На рис. 2.8 изображены нормальные кривые при различных значениях и а 0 . Чертеж наглядно иллюстрирует, как изменение параметра сказывается на форме нормальной кривой.

101

f x

7,5

Рис. 2.8.

Замечание 1. Общим называют нормальное распределение с произвольными параметрами а и 0 .

Нормированным (стандартным) называют нормаль-

ное распределение с параметрами а 0 и 1. Плотность нормированного распределения

	1		x 2
x
			2 .
		e

	2
	2

Эта функция табулирована (приложение 1).

Замечание 2. Функция F(x) общего нормального распределения определяется равенством

			x	t a 2
F (x)	1		x	2 2 dt,
	1		e
			e
		2

а функция нормированного распределения

		1		x		t 2
F (x)		1		x	e	2 dt,


	0	2
		2

			x a
Легко проверить, что	F (x) F					.
Легко проверить, что	F (x) F					.
		0

102

Замечание 3. Существует связь между функциями общего и нормированного распределения F(x), F0(x) и функцией Лапласа Ф(x):

x a
F (x) 0,5 Ф		;


F0 (x) 0,5 Ф(x).
Данные равенства позволяют		вычислять значения

F (x) и F0 (x) по таблице значений Ф(x) (приложение 3).

Вероятностный смысл параметров а и Теорема. Для нормально распределенной случайной

величины справедливы равенства:

M X a; D X 2

Доказательство. 1. По определению математического ожидания непрерывной случайной величины,

x a 2

x z a

M ( X )

xf x dx

2 2

x a

z 2

z a e

2 dz

2 dz.

Первое из слагаемых равно нулю (под знаком интеграла нечетная функция; пределы интегрирования симметричны относительно начала координат). Второе из слагаемых

равно а интеграл

Пуассона e 2

dz 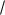2 .

Итак, M ( X ) a, т.е. математическое ожидание нормального распределения равно параметру а.

2. По определению дисперсии непрерывной случайной величины, учитывая, что M ( X ) a, имеем

103

x a 2

D( X )

a 2 e

2 2 dx

x a z

x a

z ze

2 dz.

dx dz

Интегрируя по частям, положив u z, d ze

dz, найдем

D( X ) 2 .

Следовательно,

( X ) 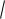D( X ) 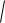2 .

Итак, среднее квадратическое отклонение нормального распределения равно параметру .

Вероятность попадания в заданный интервал нормальной случайной величины

Теорема. Вероятность того, что непрерывная случайная величина, распределенная по нормальному закону, примет значение на интервале , , равна

где Ф(x) – функция Лапласа.

Доказательство. Из свойств функции распределения известно, что P X F F . Так как случайная величина распределена нормально, то ее функция распределения

связана с функцией Лапласа равенством

(замечание 3).

Таким образом, искомая вероятность

	x a
	F (x) 0,5 Ф

P X 0,5 Ф

0,5 Ф

Вычисление вероятности заданного отклонения

Часто требуется вычислить вероятность того, что отклонение нормально распределенной случайной величины

104

X по абсолютной величине меньше заданного положительного числа δ, т.е. требуется найти вероятность осуществления неравенства X a .

Теорема. Вероятность того, что отклонение нормально распределенной случайной величины по абсолютной величине меньше положительного числа , находится из соотношения

P	X a

		2Ф	.

Доказательство.

Заменим

неравенство

X a

равно-

сильным ему двойным неравенством

X a , или

a X a .

Пользуясь предыдущей теоремой

X a

P a X a

Ф a a Ф

a a

приняв во внимание равенство

(функция Лапласа – нечетная), окончательно имеем

X a

2Ф

Правило трех сигм

Преобразуем формулу

положив t . В итоге получим

P X a t 2Ф t .

Если t=3 и , следовательно, t 3 , то

P X a 3 2Ф 3 2 0,499 0,998,

т.е. вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,998.

105

Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна 0,002 7. Это означает, что лишь в 0,27 % случаев так может произойти. Такие события исходя из принципа невозможности маловероятных событий можно считать практически невозможными. В этом и состоит сущность правила трех сигм: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.

На практике правило трех сигм применяют так: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведенном правиле, выполняется, то есть основание предполагать, что изучаемая величина распределена нормально; в противном случае она не распределена нормально.

Решение типовых задач Задача 1. Поезда метро идут строго по расписанию.

Интервал движения – 5 минут. Составить f(x) и F(x) случайной величины X – времени ожидания очередного поезда и построить их графики. Найти M(X), D(X).

Решение. Случайная величина X – время ожидания очередного поезда. Величина X распределена равномерно на отрезке [0,5], поэтому воспользуемся формулами

	0,

x a
F (x)		,
F (x)		,
b a
	1,

x a;

a x b;

f (x)

x b;

	0,
	1
	1	,


b a
	0,

x a;

a x b;

x b.

Тогда имеем

106

F (x) x ,51,

x 0;	0,

	1
0 x 5; f (x)			,
0 x 5; f (x)		5	,
x 5.		5
x 5.	0,

x 0;

0 x 5;

x 5.

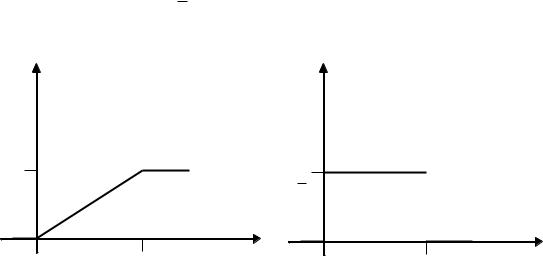
F x

f x

Математическое ожидание и дисперсия вычисляются по формулам:

M ( X )			b a	; D( X )		b a 2 .
M ( X )				; D( X )		b a 2 .
		2				12
Тогда
M ( X )	5 0	2,5;		D( X )	5 0 2		25	2,08.
M ( X )	2	2,5;		D( X )		12	12	2,08.
	2					12	12

Задача 2. Непрерывная случайная величина распределена по показательному закону с параметром 2. Составить функцию распределения, функцию плотности этой случайной величины. Найти числовые характеристики и вероятность того, что случайная величина попадет в ин-

тервал (0,3;1).

Решение. Очевидно, искомая плотность распределения

	0, при	x 0;

f (x)	2e 2x , при	x 0.
	2e 2x , при	x 0.

Искомая функция распределения

	0,	при	x 0;

F (x)		2x , при
	1 e	2x , при	x 0.

По условию 2. Следовательно,

107

34 и меньше 40;

M ( X ) x	1	1	0,5;	D( X )	1		1		0,25.
		2				2	2	2

Для нахождения вероятности P(0,3<X<1) воспользуемся формулой P a X b e a e b .

Тогда, P 0,3 X 1 e 2 0,3 e 2 1 e 0,6 e 2 0,549 0,135 0,414.

Задача 3. Детали, выпускаемые цехом, по размеру диаметра распределены по нормальному закону. Стандартная длина диаметра детали равна а=35, среднее квадратическое отклонение Требуется:

а) составить функцию плотности вероятностей; б) найти вероятность того, что диаметр наудачу взятой детали будет больше

в) найти вероятность того, что диаметр детали отклонится от стандартной длины не больше чем на

Решение. 1. Так как непрерывная случайная величина X распределена по нормальному закону, есть ее плотность распределения вероятностей выражается формулой

																		x a 2
											1								2 2			.
											1
									f (x)						e
									f (x)				2		e
Следовательно,
											1						x 35 2
											1									32 .
									f (x)					e

												2
								4				2
2. Для нормально распределенной случайной величины
													a									a
						P			X Ф											Ф		.
						P			X Ф											Ф		.

Тогда
			40 35						34 35
P 34 X 40 Ф							Ф				Ф 1,25 Ф 0,25 0,394 4 0,098 7 0,493 1.
P 34 X 40 Ф							Ф				Ф 1,25 Ф 0,25 0,394 4 0,098 7 0,493 1.
					4				4
3. Последнее задание решаем по формуле
									P	X a

																2Ф					.
Таким образом,
Таким образом,
				2
				2
P	X 35	2 2Ф			2Ф 0,5			0,3829 ,
P	X 35	2 2Ф			2Ф 0,5			0,3829 ,
				4
108				4
108

где Ф(x) – интегральная функция Лапласа (приложение 3).

Задачи (61 – 70)

В задачах 61 – 70. Случайная величина X имеет нормальное распределение с параметрами M ( X ) и ( X ). Требуется:

1.Составить функцию плотности распределения и построить ее график.

2.Найти вероятность того, что случайная величина в результате испытания примет значение, принадлежащее интервалу ; .

3.Найти вероятность того, что абсолютная величина отклонения значений случайной величины от ее математического ожидания не превысит .

61.M ( X ) 375; ( X ) 25; 300; 425; 0,1.

62.M (X ) 10; (X ) 2; 5; 12; 5.

63.M ( X ) 164; (X ) 5,5; 153; 170; 0,1.

64.M ( X ) 5; ( X ) 0,81; 4; 7; 2.

65.M (X ) 20; (X ) 0,5; 19; 25; 1,5.

66.M ( X ) 10; ( X ) 4; 12; 14; 0,1.

67.M ( X ) 25; (X ) 4; 13; 30; 0,1.

68.M (X ) 4,5; ( X ) 0,05; 3,5; 4,35; 0,1.

69.M ( X ) 16; ( X ) 100; 15,75; 16,3; 16,25.

70.M ( X ) 12; ( X ) 4; 10; 14; 5.

2.5. Закон больших чисел

Закон больших чисел это совокупность утверждений, что с вероятностью, как угодно близкой к единице (нулю), отклонение средней арифметической достаточно большого числа случайных величин от постоянной средней

109

xk 1 , …,

арифметической их математических ожиданий не превзойдет (будет больше) сколь угодно малого числа ε>0.

Неравенства Маркова и Чебышева

Теорема. Пусть случайная величина X принимает только неотрицательные значения и имеет конечное математическое ожидание M(X). Тогда для любого δ>0 имеют место неравенства Маркова:

P( X ) 1	M ( X )	, P( X )	M ( X )	.

Доказательство. Пусть закон распределения дискретной случайной величины X задан таблицей

X	x1	x2	…	xk	xk 1	…	xn
P	p1	p2	…	pk	pk 1	…	pn

Выберем и зафиксируем δ>0. Предположим, что x1 , x2 , …, xk не превосходят δ, т.е. xi для i (1; k) , а все

xn >δ, т.е. xi >δ, для i (k 1; n) .

Тогда

M ( X ) x1 p1 x2 p2 ... xk pk xk 1 pk 1 ... xn pn .

Сумма xk 1 pk 1 ... xn pn M ( X ) . Это неравенство лишь уси-

лится, если заменить каждое из	значений xk 1 , …, xn
меньшей величиной δ, следовательно,
δ( pk 1 +…+ pn ) M ( X ) ;
pk 1 +…+ pn	M ( X )	.

Сумма в левой части неравенства по теореме о сумме несовместных событий дает вероятность того, что X>δ,

т.е. P(X>δ) = P(X = xk 1 )+… + P(X = xn ) = pk 1 +…+ pn следо-

вательно P( X ) M ( X ) .

Так как сумма противоположных событий равна единице, то

110

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 2211 12 13 14 15 16 17 18 19 20 21 22 > Следующая >>>

Соседние файлы в предмете Теория вероятностей и математическая статистика

#
20.06.20142.51 Mб6Вопросы к экзамену 2011.JPG
#
20.06.2014877.57 Кб57Решение РГЗ Вариант 18.doc
#
20.06.20142.24 Mб325Теория и разбор типовых задач.pdf