
Теория и разбор типовых задач
.pdf0, |
x 2, |
|
2 x 3, |
F x x 2 3 , |
|
1, |
x 3. |
|
|
|
|
2, |
2,5. |
53. Случайная величина X задана функцией распределения вероятностей F(x).
Требуется:
1.Найти функцию плотности распределения f(x).
2.Найти M(X).
3.Найти вероятность P X .
4.Построить графики f(x) и F(x).
0, |
|
|
x 1, |
|||
|
|
|
|
1 |
|
|
1 |
|
|
|
|||
F x |
|
|
x |
|
, -1 x |
2, |
3 |
|
3 |
||||
|
|
|
x 2. |
|
||
1, |
|
|
|
|||
|
|
|
|
|
|
|
0,5, |
1,5. |
54. Случайная величина X задана функцией распределения вероятностей F(x).
Требуется:
1.Найти функцию плотности распределения f(x).
2.Найти M(X).
3.Найти вероятность P X .
4.Построить графики f(x) и F(x).
0, |
x 3, |
|
|
x 3 2 |
|
|
||
F x |
|
, 3 x 5, |
|
|
4 |
1, |
x 5. |
|
|
|
|
3, |
4. |
55. Случайная величина X задана функцией распределения вероятностей F(x).
Требуется:
1. Найти функцию плотности распределения f(x).
91
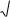
2.Найти M(X).
3.Найти вероятность P X .
4.Построить графики f(x) и F(x).
0, |
x 0, |
|||
|
|
|
|
|
x3 |
|
|||
F x |
|
, |
0 x 3, |
|
27 |
||||
|
|
x 3. |
||
1, |
||||
|
|
|
|
|
1, |
2. |
56. Случайная величина X задана функцией распределения вероятностей F(x).
Требуется:
1.Найти функцию плотности распределения f(x).
2.Найти M(X).
3.Найти вероятность P X .
4.Построить графики f(x) и F(x).
0, |
|
|
x 1, |
|
||
|
|
|
|
|
|
|
1 |
2 |
|
||||
F x |
|
|
x |
|
x , 1 x |
2, |
|
|
|
||||
|
2 |
|
|
|
|
|
1, |
|
|
x 2. |
|
||
|
|
|
|
|
|
|
0,5, |
1,5. |
57. Случайная величина X ния вероятностей F(x).
Требуется:
1.Найти функцию плотности распределения f(x).
2.Найти M(X).
3.Найти вероятность P X .
4.Построить графики f(x) и F(x).
0, |
|
|
x 2, |
|
|
|
|
|
|
|
x 2, |
2 x 3, |
||
F x |
||||
1, |
|
|
x 3. |
|
|
|
|
|
|
2,25, |
4. |
58. Случайная величина X задана функцией распределения вероятностей F(x).
Требуется:
92
1.Найти функцию плотности распределения f(x).
2.Найти M(X).
3.Найти вероятность P X .
4.Построить графики f(x) и F(x).
0, |
x 0, |
|
|
3 , |
0 x 1, |
F x x |
||
1, |
|
x 1. |
|
|
|
|
|
|
2, |
|
1 |
. |
|
2 |
||||
|
|
|
59. Случайная величина X задана функцией распределения вероятностей F(x).
Требуется:
1.Найти функцию плотности распределения f(x).
2.Найти M(X).
3.Найти вероятность P X .
4.Построить графики f(x) и F(x).
0, |
x 0, |
|||
|
|
|
|
|
x2 |
|
|||
F x |
|
, |
0 x 2, |
|
4 |
||||
|
|
x 2. |
||
1, |
||||
|
|
|
|
|
1, |
6. |
60. Случайная величина X задана функцией распределения вероятностей F(x).
Требуется:
1.Найти функцию плотности распределения f(x).
2.Найти M(X).
3.Найти вероятность P X .
4.Построить графики f(x) и F(x).
|
0, |
|
x 4, |
F x |
x 4 2 |
, |
4 x 5, |
|
|
|
|
|
1, |
|
x 5. |
|
|
|
|
|
|
|
|
93

2, |
4,5. |
2. 4. Основные законы распределения непрерывных случайных величин
Равномерное распределение
Непрерывная случайная величина X называется равномерно распределенной на отрезке a; b , если плотность вероятности постоянна на этом отрезке и равна нулю вне этого отрезка
|
0, |
при x a, |
f x |
c, при a x b, |
|
|
|
|
|
0, |
при x b. |
|
|
|
Из свойств функции плотности известно, что f x dx 1.
b
Тогда cdx 1.
a
Следовательно, с b a 1 и c b 1 a .
Таким образом, плотность f(x) равномерного распределения имеет вид
0, при x a,
f x 1 , при a x b,b a
0,
Восстановим функцию распределения F(x) равномерно распределенной случайной величины. Для этого воспользуемся формулой
x
F x f x dx .
Тогда:
x
при x a , F x 0dx 0 ;
94
при |
a x b , |
F x |
a |
x |
1 |
|
x a |
; |
|
||||
0dx |
|
|
dx |
|
|||||||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
a b |
a |
|
b a |
|
|||
при |
x b , |
F x |
a |
b |
1 |
|
|
x |
|
b a |
1 . |
||
0dx |
|
dx 0dx |
|||||||||||
|
|
|
|||||||||||
|
|
|
|
|
a b a |
|
b |
|
b a |
|
|||
Таким образом, функция распределения примет вид:
0, при x a;
F x x a , при a x b;b a
1,
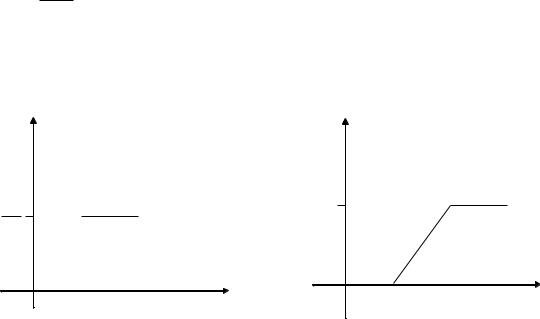
f(x) |
F(x) |
1 |
1 |
|
b a
|
|
|
|
|
|
0 |
a |
b |
x |
|
0 |
a |
b |
x |
|||||||
|
|
|
|
|||||||
Изобразим графики обеих функций (рис.2.5).
Рис. 2.5.
Теорема. Для вычисления M(X) и D(X) равномерно распределенной случайной величины имеют место равенства
|
M (X ) |
a b |
; D(X ) |
b a 2 . |
|
|
||||||||
|
|
|
|
|
||||||||||
|
|
|
|
2 |
|
|
|
|
|
12 |
|
|
|
|
Доказательство. |
|
|
Согласно |
определению |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M ( X ) |
xf x dx .Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
1 |
|
|
|
x2 |
|
b |
|
b2 a 2 |
a b |
. |
||
|
|
|
|
|
||||||||||
|
M ( X ) x |
|
dx |
|
|
|
a |
|
|
|
|
|||
|
b a |
2 b a |
2 b a |
2 |
||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Согласно определению D(X ) M (X 2 ) [M (X )]2 . Тогда
95
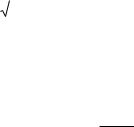
|
|
|
b |
|
|
|
|
|
|
|
|
2 |
|
|
|
3 |
|
|
a b |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
D( X ) x2 |
|
1 |
|
dx |
a b |
|
|
x |
|
|
b |
|
|
|
|||||||||
|
|
|
|
|
|
|
3 b a |
|
|
|
||||||||||||||
|
|
|
a |
b |
a |
|
|
|
4 |
|
|
a |
4 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b3 a3 |
a b 2 |
|
|
b2 ab a2 |
a b 2 |
b2 2ab a2 |
|
b a 2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 . |
|
3 b a |
4 |
|
|
|
|
3 |
|
4 |
|
|
|
12 |
|
|
||||||||||
Очевидно, что ( X ) |
b |
a |
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема. Пусть непрерывная случайная величина распределена равномерно на отрезке a; b , и отрезок c; d a; b ,
тогда
P c X d d c . b a
Доказательство. Согласно свойствам функции распределения
P c X d F d F c |
d a |
|
c a |
|
d c |
. |
b a |
b a |
|
||||
|
|
|
b a |
|||
Таким образом, для того, чтобы полностью описать непрерывную случайную величину, имеющую равномерное распределение, достаточно знать концы отрезка, которому принадлежат все возможные значения этой случайной величины.
Показательное распределение
Показательным (экспоненциальным) называют рас-
пределение вероятностей случайной величины X, которое описывается плотностью
0 |
при x 0; |
|
|
|
|
f x |
x |
при x 0, |
e |
||
|
|
|
где - постоянная положительная величина. Показательное распределение определяется одним па-
раметром . Эта особенность показательного распределения указывает на его преимущество по сравнению с распределениями, зависящими от большего числа параметров. Обычно параметры неизвестны и приходится находить их оценки (приближенные значения); разумеется, проще оценить один параметр, чем два или три и т.д.
96
Найдем функцию распределения показательного зако-
|
|
|
|
|
|
|
x |
на. Воспользуемся формулой |
F x f x dx . Тогда: |
||||||
|
|
|
|
|
|
|
|
- при |
|
F x |
x |
|
; |
|
|
x 0, |
0dx 0 |
|
|
||||
|
|
|
|
|
|
|
|
- при |
|
F x |
0 |
x |
e x dx 1 |
e x . |
|
x 0, |
0dx |
||||||
|
|
|
|
0 |
|
|
|
Итак, |
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
при x 0; |
|
|
|
|
|
|
|
|
|
|
|
|
F x |
e x , при x 0. |
||
|
|
|
|
|
1 |
||
|
|
|
|
|
|
|
|
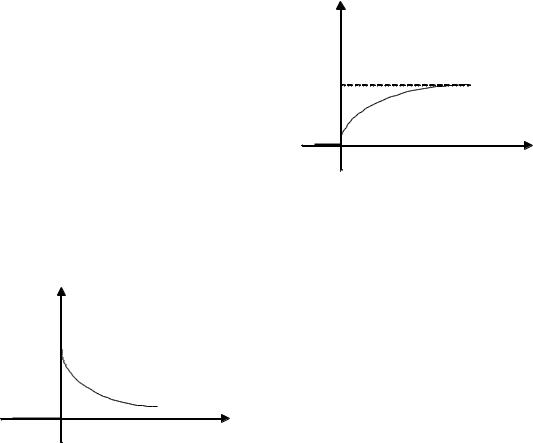
Графики плотности и функции распределения показа-
F(x)
1
0 |
x |
тельного закона изображены на рис. 2.6.
f (x)
0 x
Рис. 2.6.
97
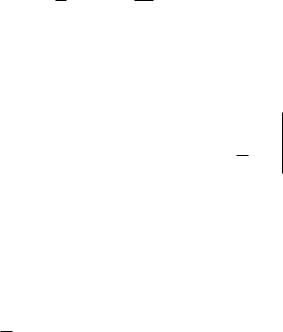
Теорема. Для M(X) и D(X)
ния справедливы равенства
M ( X ) 1 ;
Доказательство. Согласно
показательного распределе-
D( X ) 1 .2
определению M ( X ) xf x dx .
Тогда,
M X |
|
|
|
|
|
|
|
|
|
|
||
x e |
x dx x e x dx |
|||||||||||
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
x |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
||||||||||
|
|
e x |
|
|
e |
x dx |
|
|
||||
|
|
|
|
2 |
||||||||
|
|
|
|
0 |
|
0 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||||
u x; du dx
dv e x ; V 1 e e
|
|
|
|
1 |
0 1 |
1 |
|
|
|
|
|
||||||
e |
x |
|
|
|
|
|
. |
|
|
|
0 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Соотношение D X |
1 |
предлагается доказать самостоя- |
|
2 |
|||
|
|
||
тельно. |
|
||
Очевидно, что X 1 , т.е. математическое ожидание и
среднее квадратическое отклонение показательного распределения равны между собой.
Теорема. Вероятность попадания в интервал показательно распределенной случайной величины вычисляется по формуле
P a X b e a e b .
Доказательство. Используем формулу
P a X b F b F a .
Учитывая, что F a 1 e a , F b 1 e b , получим
P a X b e a e b .
98

Нормальное распределение
Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью
|
|
|
|
|
|
x a 2 |
|
f x |
1 |
|
e |
2 2 |
. |
||
|
|
||||||
|
|
|
|
||||
2 |
|
|
|
||||
Данное распределение определяется двумя параметрами: а и , достаточно знать эти параметры, чтобы задать нормальное распределение.
График плотности нормального распределения называ-
ют нормальной кривой (кривой Гаусса).
Исследуем и построим график функции
|
|
|
|
|
|
|
x a 2 |
|
||
|
|
1 |
|
|
2 2 |
|||||
|
|
|
|
|||||||
|
f x |
|
|
e |
|
|||||
|
2 |
|
|
|
|
|
|
|||
1. |
Очевидно, функция определена на всей оси абсцисс. |
|||||||||
2. |
При всех значениях x функция принимает положи- |
|||||||||
|
тельные значения, т.е. нормальная кривая располо- |
|||||||||
|
жена над осью Оx. |
|
|
|
|
|
|
|
||
3. |
Предел функции при неограниченном возрастании x |
|||||||||
|
(по абсолютной величине) равен нулю: lim f x 0 , т.е. |
|||||||||
|
|
|
|
|
|
|
|
|
x |
|
ось Оx служит горизонтальной асимптотой графика.
4.Исследуем функцию на экстремум. Найдем первую производную:
|
|
|
x a |
|
|
x a 2 |
|||
|
|
f x |
|
|
|
||||
|
|
e |
2 2 . |
||||||
|
|
|
|||||||
|
|
|
|
||||||
|
|
|
3 |
2 |
|
|
|
|
|
Очевидно, что: |
|
|
|
|
|
|
|
||
при |
x a, |
f x 0; |
|
|
|
|
|
|
|
при |
x a, |
f x 0; |
|
|
|
|
|
|
|
при |
x a, |
f x 0. |
|
|
|
|
|
|
|
Следовательно: |
|
|
|
|
|
|
|
||
при |
x ; a , f x - возрастает; |
|
|
|
|||||
99 |
|
|
|
|
|
|
|
|
|
при x a; , f x - убывает;
при ( x a ) функция имеет максимум
f a |
1 |
|
||
|
|
|
||
|
|
|
||
2 . |
||||
|
||||
5.Разность ( x a ) содержится в аналитическом выражении функции в квадрате, т.е. график функции симметричен относительно прямой x a.
6.Исследуем функцию на точки перегиба. Найдем вторую производную:
|
|
|
|
|
|
|
x a 2 |
|
|
x a 2 |
|||
y |
|
|
1 |
|
|
2 |
2 |
|
|||||
|
|
|
|
|
e |
|
1 |
|
|
|
. |
||
|
|
|
|
|
|
|
|
||||||
|
3 |
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Легко видеть, что при x a и x a вторая производная равна нулю, а при переходе через эти точки она меняет
знак (в обеих этих точках значение функции равно 1 ).
 2e
2e
f x
1
 2 1
2 1
 2 e
2 e
0 |
a |
а |
a |
|
|
x |
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
||
Таким образом, точки графика a , |
|
|
|
|
|
|
и a , |
|
|
|
|
|
яв- |
|||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 e |
|
|
2 e |
|
|||||||
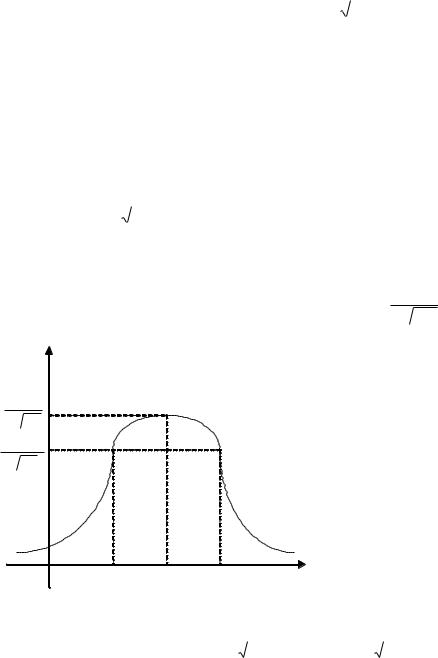
ляются точками перегиба. На рис. 2.7 изображена нормальная кривая
Рис. 2.7.
Влияние параметров нормального распределения на форму нормальной
100
