
Теория и разбор типовых задач
.pdf
Если выборка имеет достаточно большой объем и является репрезентативной, то заключение о тесноте связи признаков X и Y может быть распространено на всю генеральную совокупность.
Так, для оценки коэффициента корреляции rГ нормально распределенной совокупности можно использовать формулу
|
1 r |
2 |
|
|
|
1 r |
2 |
. |
|||
r 3 |
|
В |
r |
Г |
r |
3 |
|
В |
|||
|
|
|
|
|
|||||||
В |
|
n |
|
|
В |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Уравнения регрессии в случае равноотстоящих значений признаков
В случае, если значения хотя бы одного из признаков являются равностоящими, полезно использовать условные варианты.
Пусть для определенности значения признака X являются равноотстоящими. Тогда расчет основных параметров уравнения регрессии производится по алгоритму:
1. Рассчитываем условные варианты
ui xi C , h
где С – ложный нуль, h – шаг.
2. Находим условные эмпирические моменты первого и второго порядка:
M1* |
u n |
|
|
M 2* |
u 2n |
|
|
|
|
|
|||||
|
|||||||
i i u; |
i i u 2 . |
||||||
|
n |
|
n |
||||
3. Находим
x M1*h C uh C;
x 
 u 2 u 2 h u h.
u 2 u 2 h u h.
4.Вычисляем rB uy u y .
u y
161

Пусть значения обоих признаков X и Y являются равноотстоящими соответственно с шагом h1 и h2 . Тогда целесообразно воспользоваться следующим алгоритмом:
1. Переходим к условным вариантам
|
|
x |
C |
; i |
|
y j C2 |
. |
||||||||
|
ui |
i |
1 |
|
|
|
|
|
|||||||
|
|
h1 |
|
|
h2 |
||||||||||
|
|
|
|
|
|
|
|
|
|||||||
2. |
Находим условные эмпирические моменты |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
; u2 |
и 2 . |
|
|||||
|
|
|
|
u и |
|
||||||||||
3. |
Находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x uh1 C1; x u h1; y vh2 C2 ; y v h2
4. Коэффициент корреляции определяется по формуле
r uv u . |
|
B |
u v |
|
|
5. Составляем уравнения регрессии.
Криволинейная корреляция
Между признаками X и Y могут существовать и нелинейные корреляционные зависимости (параболическая, гиперболическая, показательная и пр.).
Рассмотрим подробнее случаи параболической и гиперболической зависимости. Предположим между признаками X и Y – параболическая корреляционная связь. Тогда уравнения регрессии имеют вид:
Y x a1x2 a2 x a3 ;
X y b1 y 2 b2 y b3 .
Основываясь на выше описанном методе «наименьших квадратов», получим следующую систему линейных уравнений для нахождения параметров:
162
a1 x 4 a2 x3 а3 x 2 x 2 y;
a1 x3 a2 x 2 a3 x xy;
a1 x 2 a2 x a3 y.
Решением системы являются «наилучшие» параметры искомой параболы. Для нахождения параметров b1 , b2 , b3 необходимо составить идентичную систему уравнений.
В случае гиперболической корреляционной зависимости Y от X уравнения регрессии имеют вид:
Y x ax1 a2 ; X y by1 b2 .
Метод "наименьших квадратов" приводит процесс составления уравнения регрессии к решению следующей системы:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
1 |
1 |
||||||||||
a |
|
|
|
|
a |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|||||||||||
|
1 |
|
|
|
|
|
|
2 |
|
|
|
||||
|
x |
2 |
|
|
|
x |
|
x |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
a |
|
|
|
a |
2 |
y. |
|
|
|
|||||
|
|
|
|
||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
y ;
Аналогично составляется и решается система уравнений относительно параметров b1 и b2 .
Для оценки тесноты нелинейной корреляционной связи используют выборочные корреляционные отношения:
yx выборочное корреляционное отношение Y к X; xy
выборочное корреляционное отношение X к Y.
Выборочным корреляционным отношением Y к X на-
зывают отношение межгруппового среднего квадратического отклонения к общему среднему квадратическому отклонению признака Y:
yx |
межгр |
|
общ |
||
|
или в других обозначениях
163

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yx |
y |
x |
. |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
||||||||
Здесь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nx |
|
x |
|
2 |
|
|
|
|
|
|
|
|
|
|
ny y |
|
2 |
||
|
|
|
|
|
|
y |
y |
|
|
|
|
|
|
|
|
|
|
y |
|||||||
y |
|
|
|
|
|
|
; y |
||||||||||||||||||
x |
|
n |
|
|
, |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|||||||||
где n – объем выборки (сумма всех частот); n x - частота значения x признака X; n y - частота значения y признака Y; y - общая средняя признака X; y x - условная средняя при-
знака Y.
Аналогично определяется выборочное корреляционное отношение X к Y:
xy x y .
x
Свойства выборочного корреляционного отношения
Поскольку xy обладает тем же свойством, что и yx , пе-
речислим свойства только выборочного корреляционного отношения yx , которое далее для упрощения записи бу-
дем обозначать через и для простоты называть «корреляционным отношением».
С в о й с т в о 1. Корреляционное отношение удовлетворяет двойному неравенству
01.
Св о й с т в о 2. Если 0, то признак Y с признаком X корреляционной зависимостью не связан.
Св о й с т в о 3. Если 1, то признак Y связан с признаком X функциональной зависимостью.
Св о й с т в о 4. Выборочное корреляционное отношение не меньше абсолютной величины выборочного коэффициента корреляции: rВ .
Св о й с т в о 5. Если выборочное корреляционное отношение равно абсолютной величине выборочного коэф-
164

фициента корреляции, то имеет место точная линейная корреляционная зависимость.
Другими словами, если rВ , то точки x1; y1 , x2 ; y2 , ,xn ; yn лежат на прямой линии регрессии, найденной способом "наименьших квадратов".
Понятие множественной корреляции
Множественная корреляция это исследование связи между несколькими признаками.
Пусть Z линейно зависит от X и Y, тогда уравнение линейной множественной регрессии имеет вид:
z a1x a2 y a0 .
Коэффициенты множественной регрессии а1 , а2 , и а0 находятся методом "наименьших квадратов", т.е. так, что-
бы функция F a1, a2 , a0 a1xi a2 yi a0 zi 2 ni имела минимум.
i
Раскрывая знак суммы и группируя слагаемые, приводим уравнение к виду:
z z a1 x x a2 y y ,
причем коэффициенты регрессии определяются равенствами:
a |
|
|
rxz ryz rxy |
|
|
z |
; a |
|
|
ryz rxz rxy |
|
|
z |
, |
|
|
|
2 |
|
|
|||||||||
|
|
|
|
|
|
|
||||||||
1 |
|
1 rxy2 |
|
x |
|
1 rxy2 |
|
y |
||||||
|
|
|
|
|
|
|
||||||||
где rxz ; ryz и rxy |
коэффициенты корреляции соответствен- |
|||||||||||||
но между признаками X и Z; Y и Z; X и Y.
Теснота линейной корреляционной связи признака Z с X
и Y оценивается с помощью выборочного совокупного ко-
эффициента корреляции:
|
r 2 |
2r |
r |
r |
yz |
r 2 |
|
R |
xz |
xy |
xz |
|
yz |
. |
|
|
1 r 2 |
|
|
|
|||
|
|
|
|
|
|
||
|
|
|
xy |
|
|
|
|
165 |
|
|
|
|
|
|
|

При этом 0 R 1 и при приближении R к единице теснота линейной связи Z с X и Y увеличивается.
Следующей задачей множественной корреляции является задача оценить влияние на Z отдельно признака X и отдельно признака Y. Это осуществляется при помощи
выборочных частных коэффициентов корреляции:
rxz y |
|
rxz |
rxy z yz |
|
; |
ryz x |
|
ryz |
rxy rxz |
|
. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
r |
2 |
|
r |
2 |
|
|
r |
2 |
|
r |
2 |
||||||||
|
|
1 |
|
1 |
|
|
|
|
|
1 |
|
1 |
|
|
|
||||||
|
|
|
|
|
xy |
|
yz |
|
|
|
|
|
|
|
xy |
|
xz |
|
|
||
Первый коэффициент оценивает тесноту линейной корреляционной связи между Z и X, когда Y остается постоянным. Теснота связи между Z и Y (при постоянной X) оценивается вторым коэффициентом корреляции ryz x .
Эти коэффициенты имеют те же свойства, что и обыкновенный выборочный коэффициент корреляции.
Решение типовых задач Задача 1. Выборочно обследовано 100 заводов по вели-
чине основных производственных фондов X (млн. руб.) и объему готовой продукции Y (млн. руб.). Результаты представлены в корреляционной таблице (табл. 1).
Таблица 1
Y |
|
|
X |
|
|
n y |
|
5 |
15 |
25 |
35 |
45 |
|
30 |
7 |
1 |
|
|
|
8 |
32 |
2 |
7 |
1 |
|
|
10 |
34 |
1 |
5 |
4 |
1 |
|
11 |
36 |
|
1 |
15 |
10 |
8 |
34 |
38 |
|
|
3 |
12 |
15 |
30 |
40 |
|
|
|
1 |
6 |
7 |
n x |
10 |
14 |
23 |
24 |
29 |
n=100 |
По данным исследования требуется:
166

1)в прямоугольной системе координат построить эмпирические ломаные регрессии Y на X и X на Y;
2)оценить тесноту линейной корреляционной связи;
3)составить линейные уравнения регрессии Y на X и X на Y и построить их графики в одной системе координат.
Решение. 1. Так как при x = 5 признак Y имеет распределение
|
|
|
|
Y |
|
3 |
|
32 |
34 |
|
|
||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
ni |
|
7 |
|
|
2 |
|
1 |
|
|
||||||
то условное среднее |
|
x 5 |
|
30 7 32 2 34 1 |
30,8. |
||||||||||||||
y |
|||||||||||||||||||
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|||
При x=15 признак Y имеет распределение |
|||||||||||||||||||
|
Y |
|
3 |
|
32 |
|
34 |
|
36 |
|
|||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
ni |
|
1 |
|
|
|
7 |
|
5 |
|
1 |
|
|||||||
Cледовательно y x 15 301 32 7 34 5 361 32,86. 14
Аналогично вычисляются все условные средние y x . В результате получим таблицу, выражающую корреляционную зависимость y от X (табл. 2).
Таблица 2
X |
5 |
15 |
25 |
35 |
45 |
||
|
|
|
30 |
32, |
35, |
37, |
37, |
|
y x |
||||||
|
|
|
,8 |
86 |
74 |
08 |
86 |
Так как при y=30 признак X имеет распределение
X |
5 |
15 |
n j |
7 |
1 |
167

то условное среднее |
|
y 30 |
5 7 15 1 |
6,25. |
|||||||||||
x |
|||||||||||||||
|
8 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
При y = 32 признак X имеет распределение |
|||||||||||||||
|
|
|
X |
|
|
5 |
|
15 |
|
25 |
|
|
|
||
|
|
|
n j |
|
|
2 |
|
7 |
|
1 |
|
|
|
||
Следовательно |
|
y 32 |
|
5 2 15 7 25 1 |
14. |
||||||||||
x |
|||||||||||||||
|
|
|
|
10 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Аналогично вычисляются все x y . В результате получим табл. 3.
Таблица 3
|
Y |
30 |
32 |
34 |
36 |
38 |
40 |
|
|
|
|
6, |
14 |
19, |
32, |
39 |
43, |
|
x y |
|||||||
|
|
|
25 |
|
54 |
35 |
|
57 |
В прямоугольной системе координат построим точки Ai xi ; y xi , соединим их отрезками прямых, получим эмпи-
|
|
x y |
||
|
y |
|||
|
|
В6 |
||
39 |
|
В5 |
||
38 |
|
А5 |
||
37 |
|
|
|
|
|
|
А4 |
||
36 |
|
В4 |
||
|
|
А3 |
||
35 |
|
|
|
|
|
|
В3 |
||
34 |
|
|
|
|
33 |
|
А2 |
||
32 |
|
В2 |
||
31 |
|
|
|
|
30 |
А1 |
|||
|
|
В1 |
|
|
|
|
5 10 15 20 25 30 35 40 45 x(x y ) |
||
рическую линию регрессии Y на X. Аналогично строятся точки B j x y ; y j и эмпирическая линия регрессии X на Y .
168

2. Выдвинув гипотезу о линейной корреляционной зависимости, оценим тесноту связи. Вычислим выборочный коэффициент корреляции
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
xy x y |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
x |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
n |
|
|
y j n j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
n |
|
|
|
|
|
|
|
|
y 2j |
n j |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
i |
|
|
i |
, y |
|
|
|
|
|
|
|
, |
|
|
|
x2 |
|
|
|
|
|
|
|
|
i |
i |
|
, y 2 |
|
|
|
|
|
|
|
|
|
|
, |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
n |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi y j nij |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, x |
x2 |
|
, y |
y2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
xy |
|
x |
y |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 10 15 14 25 23 35 24 45 29 |
|
29,8; |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
30 8 32 10 34 11 36 34 38 30 40 7 |
35,78; |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
y |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
52 10 152 14 252 23 352 24 452 29 |
|
1059 ; |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
302 8 322 10 342 11 362 34 452 30 402 7 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
y2 |
1287,4 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
30 5 7 30 15 1 32 5 2 32 15 7 32 25 1 34 5 1 34 15 5 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
xy |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
34 25 4 34 35 1 36 15 1 36 25 15 36 35 10 36 45 8 38 25 3 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
38 35 12 38 45 15 40 35 40 45 6 |
|
1095,5 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x |
1059 (29,8)2 13,08; |
y |
|
|
|
1287,4 (35,78)2 2,68; |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
1095 ,5 29,8 35,78 |
|
0,83. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
13,08 2,68 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Так как rB |
|
|
близок к единице, |
то между Y и X имеется |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
достаточно тесная корреляционная связь. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3. Подставляя найденные величины в уравнения |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
x |
|
, |
|
y |
|
|
r |
x |
y |
|
, |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y x y r |
|
x |
X |
x |
y |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
получаем искомые уравнения регрессии: 1) уравнение регрессии Y на X
Yx 35,78 0,83 13,082,68 x 29,8 , Y x 0,17 x 30,71.
2)уравнение регрессии X на Y
X y 29,8 0,83 13,082,68 y 35,78 , X y 4,05y 115,14.
169
Замечание. Если в корреляционной таблице даны интервальные распределения,
то за значения вариант нужно брать середины частичных интервалов.
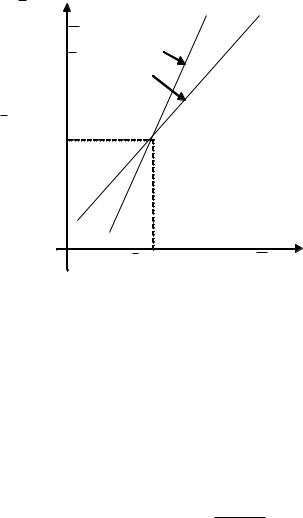
Изобразим графики прямых линий регрессии на чертеже.
Y x y
X y 4,05y 115,14.
Y x 0,17x 30,71.
y 35,78
x 29,8 |
x X y |
Так как значения признаков X и Y являются равноотстоящими, то можно данную задачу решить с помощью условных вариант.
Так, в данном примере
C1 25 , |
h1 10 , ui |
|
xi 25 |
|
10 |
|
|||
|
|
|
|
|
C2 36 , |
h2 2 , j |
|
y j 36 |
|
2 |
|
|||
|
|
|
|
|
;
.
v |
|
|
u |
|
|
n y |
|
-2 |
-1 |
0 |
1 |
2 |
|
-3 |
7 |
1 |
|
|
|
8 |
-2 |
2 |
7 |
1 |
|
|
10 |
170
