
- •1. Принцип управления. Классификация систем управления.
- •Принцип разомкнутого управления
- •Принцип регулирования по отклонению
- •2. Алгоритмы и законы регулирования
- •3. Математическое описание сау. Модели вход-выход.
- •4. Математическое описание сау. Модели вход-состояние-выход.
- •5. Математическое описание звеньев и сау. Типовые звенья.
- •6. Типовые воздействия в системе и реакция на них.
- •7. Устойчивость систем управления. Первый метод Ляпунова.
- •8. Устойчивость систем управления. Частотный критерий устойчивости.
- •9. Устойчивость систем управления. Алгебраические критерии устойчивости.
- •10. Качество установившихся процессов в линейных сау. Коэффициенты ошибок.
- •Коэффициенты ошибок
- •11. Качество установившихся процессов в линейных сау. Частотные критерии качества.
- •12. Качество установившихся процессов в линейных сау. Корневые критерии качества.
- •13. Качество установившихся процессов в линейных сау. Интегральные критерии качества.
- •14. Коррекция сау. Способы коррекции.
- •15. Коррекция сау в функции внешних воздействий. Инвариантность.
- •Коррекция по возмущающему воздействию
- •16. Задачи и методы синтеза линейных сау.
- •17. Многомерные сау.
- •18. Чувствительность систем управления.
- •Существуют методы анализа чувствительности и методы достижения малой чувствительности в проектируемых системах.
- •Определить чувствительность для системы:
- •Управляемость.
- •20. Наблюдаемость систем управления.
- •21. Дискретные системы управления. Классификация.
- •22. Импульсные системы управления.
- •23. Нелинейные системы управления. Второй метод Ляпунова.
- •24. Автоколебания нелинейных сау. Определение параметров автоколебаний.
- •Определение параметров автоколебаний
- •25. Методы линеаризации нелинейных сау.
- •26. Случайные процессы
- •27. Оптимальное управление. Постановка задачи оптимального управления. Критерии оптимальности.
- •28. Аналитическое конструирование регуляторов. Постановка задачи.
- •29. Методы теории оптимального управления
- •30. Адаптивные системы управления. Классификация адаптивных сау.
27. Оптимальное управление. Постановка задачи оптимального управления. Критерии оптимальности.
Под оптимальной САУ понимается наилучшая в некотором смысле система. Критерии оптимальности могут быть различны и зависят от решаемой задачи. Наиболее часто встречаются такие критерии оптимальности:
1) Точность САУ при изменяющемся воздействии,
2) Время переходного процесса,
3) Экономичность;
Производительность;
Интегральные критерии.
К настоящему времени наибольшее развитие получили 2 направления в теории оптимальности систем:
1) Теория оптимального управления движением систем с полной информацией об объекте и возмущениях;
Теории оптимального управления при случайных возмущениях.
Для реализации оптимального управления необходимо:
Определить цель управления. Цель выражается либо целевой функцией, либо критерием оптимизации.
Целевая функция или критерий оптимизации позволяют найти количественный эффект любого решения.
Выбрать модель для анализа и определения эффективности принятого решения.
Изучить все состояния среды функционирования объекта, влияющие на прошлое, настоящее и будущее процесса управления.
При решении задачи оптимального управления используются методы вариационного исчисления, принципы максимума, а также динамическое и математическое программирование.
Задачу оптимального управления в общем случае можно сформировать следующим образом:
Даны:
1)Цель управления, представленная математически в виде некоторого функционала или критерия управления
2)Уравнения системы - они обычно задаются в виде уравнений состояний
3)Система граничных уравнений в начальный и конечный момент времени.
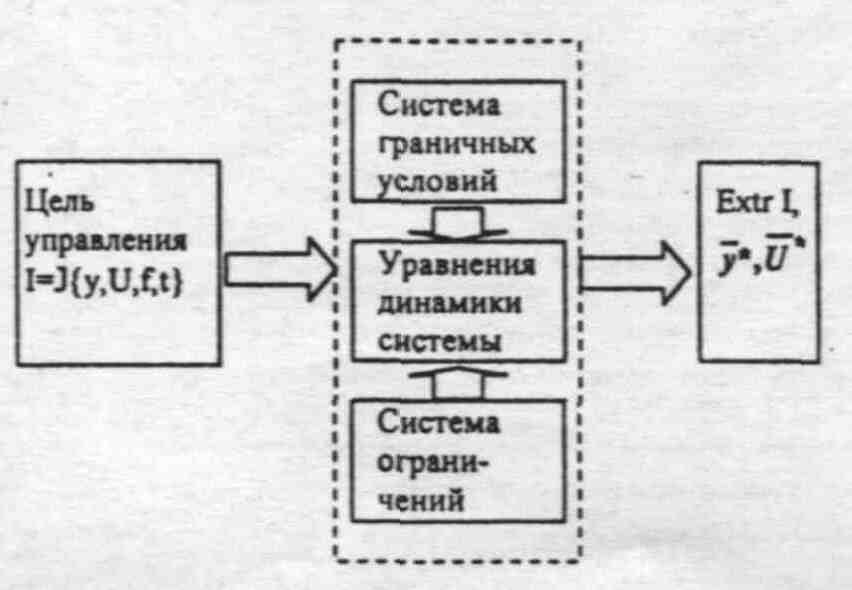
4)Система ограничений, которым должны удовлетворять переменные состояния и уравнения.
Требуется найти:
Вектор управления, при котором критерий цели управления имеет экстремум (max или min).
Необходимо отметить, что оптимальное управление в ряде случаев может не существовать, и об этом нельзя судить не решая задачу. Решение задачи нахождения оптимального управления является неоднозначным, т.е. каждое найденное решение дает локальный оптимум. Если найдены все локальные оптимумы, то в этом случае может быть выделен глобальный оптимум. Найденный глобальный оптимум является решением задачи оптимального управления.
Интегральные критерии качества:
Оптимальное Быстродействие
Функционал имеет вид
![]()
Оптимальная Производительность
Критерием оптимальности явл-ся угол поворота за определенное время t и функционал имеет вид
![]()
Оптимальная экономичность
Критерием оптимальности явл-ся расход энергии за определенное время и функционал имеет вид
![]()
28. Аналитическое конструирование регуляторов. Постановка задачи.
При исследовании качества переходных в линейных САУ вводились разлитые интегральные критерии качества, с помощью которых оценивался переходной процесс на бесконечном интервале времени. При рассмотрении интегральных критериев качества мы убедились в том, что эти критерии позволяют определить параметры регулятора, если задана его структура. Можно поставить более общую задачу: найти закон регулирования - аналитическую функцию, связывающую управляющую координату и управляющее воздействие при этом доставляющее min интегральному критерию качества. Такое оптимальное конструирование дифференциального уравнения регулятора получило название аналитического конструирования регуляторов. По методам решения и постановке задачи эта задача сродни задачам оптимального регулирования.
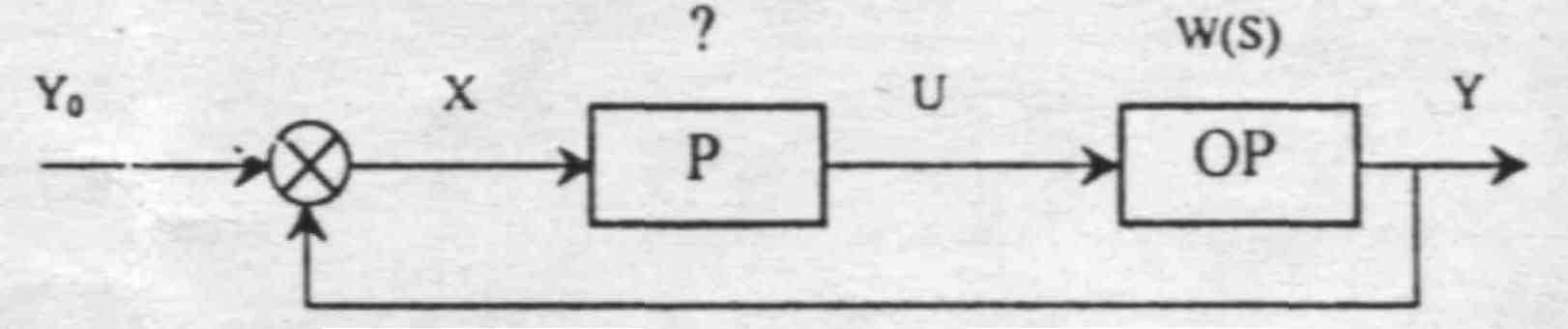
Это вариационная задача, где в качестве экстремали ищется функция связывающая Х и U.
При аналитическом конструировании задача состоит в том, что бы найти закон регулирования который с учетом уравнений объекта и граничных условий доставлял бы min интегралу, характеризующему квадратичную ошибку системы и гарантирующему ее устойчивость.
Постановка задачи оптимального конструирования регуляторов.
Объект регулирования задан с помощью дифуравнений, что в операторной форме соответствует заданию передаточной функции Wор(S) (или W(S))
Считают что на систему не действуют внешние возмущения, а переходной процесс происходит при изменении начальных условий.
![]()
![]()
X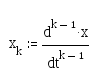 = y0
– y
- рассогласование
= y0
– y
- рассогласование
В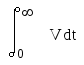 устойчивой линейной САУ в результате
переходного процесса все функции
координат должны стремиться к 0. х1()
= х2()
= … хn()
= U()
= 0 (2)
устойчивой линейной САУ в результате
переходного процесса все функции
координат должны стремиться к 0. х1()
= х2()
= … хn()
= U()
= 0 (2)
В качестве критерия оптимальности выберем интеграл вида
(3), где V- положительно определённая квадратичная форма.
![]() Т.е.
если подставитьV
в
(3) то это будет
квадратичная ошибка системы.
Т.е.
если подставитьV
в
(3) то это будет
квадратичная ошибка системы.
Член U2 в (4) характеризует стоимость процесса управления, т.е. затраты энергии на нагрев. U2 гарантирует отсутствие нереализуемых в линейных регуляторах законов, он гарантирует отсутствие управляющих воздействий, при которых скорость превращается в бесконечность.
С амо
существование
(3) гарантирует
устойчивость системы. При аналитическом
конструирование задание состоит в том
чтобы найти в аналитической форме
функцию Ф(U,U,x1…xk)
= 0 (5) – который с учётом уравнений
объекта и приграничных условий (1) и (2)
доставлял бы минимум интегралу (3).
амо
существование
(3) гарантирует
устойчивость системы. При аналитическом
конструирование задание состоит в том
чтобы найти в аналитической форме
функцию Ф(U,U,x1…xk)
= 0 (5) – который с учётом уравнений
объекта и приграничных условий (1) и (2)
доставлял бы минимум интегралу (3).
