21. Дискретные системы управления. Классификация.

К дискретным системам относятся – импульсные, цифровые и релейные.

В импульсных системах производится квантование сигнала по времени.

В релейных осуществляется квантование по уровню.

В цифровых и по времени и по уровню.

Для описания дискретных систем используются разностные уравнения.

Дискретные системы отличаются от обычных систем, тем, что в их состав помимо обыкновенных звеньев входят звенья осуществляющие одно или несколько квантований.

Линейная импульсная система состоит из одного или нескольких элементов и непрерывной части.

Для описания дискретных сигналов применяют решётчатую функцию.

НЭ – импульсный элемент.

Для импульсных систем в основном применяют 3 вида квантования сигнала по времени:

1. амплитудно-импульсная модуляция (амплитуда импульса  входному сигналу)

2. Широтно-импульсная модуляция (широта импульса  входному сигналу)

3. Фазоимпульсная модуляция (фаза импульса  входному сигналу)

Во всех случаях период чередования импульсов является постоянным

В случае амплитудно-импульсной модуляции (рис б) длительность каждого импульса постоянна, имеет одинаковое значение и обозначается ^Т (0 <  < 1). Амплитуда импульсов принимает значения x[nT]

 = им / T – скважность

Для единичного импульса, помещённого в начало координат и имеющего длительность Т можно записать

S1(t) = 1(t) – 1(t - T)

Выходная величина импульса будет определятся значением x[nT].

Аргумент (t - nT) означает сдвиг каждого импульса на величину nT

от начала координат.

В случае широтно-импульсной модуляции изменяется ширина импульса.

_n = ax[nT]

_nT – не должна превышать значение периода Т. аМ  1, х(t) < М

Величина импульса с остается постоянной и для “+” и для ”-”.

S1(t) = 1(t) – 1(t - _nT) – широтно-импульсная модуляция.(рис. г)

Фазоимпульсная модуляция.

При фазоимпульсной модуляции амплитуда импульса с и длительностью Т остаются постоянными. При этом вводится переменный сдвиг импульса по времени относительно каждого периода.

_n = ах[nT] aM  1 - 

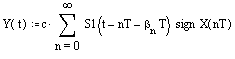
В цифровых системах управления к квантованию по времени добавляется ещё и квантование по уровню. Если обозначим за h – размер одной ступеньки квантования по уровню, тогда величина каждого значения решётчатой функции будет представляться числом ступеней: y[nT] = k*h*sign x[nT]

k – число ступеней h (целое)

Значение решётчатой функции y[nt] запоминается на весь период квантования.

22. Импульсные системы управления.

Рассмотрим импульсную систему с амплитудно-импульсн. модуляцией.

Разомкнем эту систему и расчленим условно импульсный элемент на 2 части:

┴(идеальный квантователь) - дает решетчатую ф-ию, определенную в дискретный момент времени nT

S₁(t) придает каждому импульсу Передаточ. и решетчатой функции определенную длительность

Импульсные системы описываются разностными уравнениями: Δf[n] =f[n+1] – f[n] – первая разность решетчатой функции. Первая разность от Δf[n] называется разностью 2-го порядка или второй разностью:

Δ²f[n] =Δf[n+1] – Δf[n] Δ^kf[n] =Δ^k-1f[n+1] – Δ^k-1f[n] – разность произвольного порядка.

Всякое соотношение, связывающее решетчатую функцию f[n] и её разности до некоторого порядка «k» называются разностными урав-ми.

Передаточная функция разомкнутой цепи импульсной системы – это отношение выходной величины к входной при нулевых начальных условиях.

W^*(q, ε) = .

В общем случае перед. ф-ия импульсной цепи

W^*(q, ε) =

Всоответствии со свойствамиD-преобразований, передаточная ф-ия W^*(q, ε) будет периодической вдоль мнимой оси.

q = α + jώ

т.к. ф-ия периодическая , то она будет определятся в полосе -π< ώ > π, -∞<α>∞ , ω=ώt – относительная частота

-π

Передаточная ф-ия м.б. найдена и через Z-преобразования:

z=e^q (6),

W^*(Z, ε) =

Преобразование (6) отображает основную полосу -π< ώ > π на плоскости z, причем отрезок мнимой оси q=jώ в интервале -π< ώ > π отображается в окружности единичного радиуса z=e^jώ, а левая часть этой полосы отображается – внутрь круга.

X₁ = a*sinωt X₂ = a*sin2ωt t=nT

АФЧХ разомкнутой импульсной системы определяется аналогично обыкновенной линейной системе:

W(S)→W(jω) g(t)=sinωt

Q=ST g[n]=sinώn n=t/T ώ=ωt

W^*(jώ,ε)=W^*(q, ε) – для импульсной системы.

По аналогии с непрерывными системами:

A^*(ώ,ε) = │W^*(jώ,ε)│ φ^*(ώ,ε) = argW^*(jώ,ε)