8. Задача о быстродействии.

К задачам, у которых момент времени   окончания процесса управления заранее не фиксирован, относится и задача об управлении, оптимальном по быстродействию.

Рассмотрим систему, описываемую векторным дифференциальным уравнением

(8.1)

где x,u,f — векторы следующего вида:

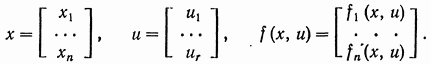
На управляющие силы   наложены ограничения

(8.2)

которые, в частности, могут иметь и такой вид:

(8.3)

Требуется найти оптимальное управление  которое за минимально возможное время Т приводит систему из начального состояния   в состояние  , то есть в начало координат в фазовом пространстве.

Минимально возможное время T, в течение которого управление приводит систему из точки   в точку  , является функцией от начального состояния системы

(8.4)

и задача о быстродействии будет, таким образом, частным случаем рассмотренной в п. 2 задачи о минимизации функционала

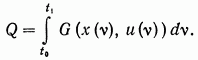
Действительно, полагая

(8.5)

найдем, что при этом функционал Q представляет собой время приведения системы из начального состояния   в состояние 

(8.6)

и, следовательно,

(8.7)

Учитывая, что в качестве начального состояния можно принять любое текущее состояние   и предполагая, что функция  непрерывна и всюду имеет непрерывные частные производные по всем своим аргументам, найдем следующее дифференциальное уравнение первого порядка в частных производных, которому удовлетворяет функция  :

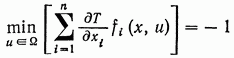
или

(8.8)

Grad- это вектор состоящий из частных производных функций который показывает направление и возрастание функции.

Уравнение (8) и является уравнением Беллмана в задаче о быстродействии.

Минимизация по u выражения в квадратных скобках в левой части (8) позволит определить оптимальное управление u*, которое будет представлено в виде функции от  . При подстановке в (8) указанного значения u* получим не содержащее и уравнение первого порядка в частных производных. Решение этого уравнения должно удовлетворять граничному условию

(8.9)

Если это решение удастся найти, то будет определено в виде явной функции от фазовых координат системы оптимальное управление u*=u*(x)

К сожалению, получить решение уравнения (8) в замкнутом виде удается лишь в простейших случаях.

9. Принцип максимума л. С. Понтрягина.

Управляемая система описывается дифференциальными уравнениями

(9.1)

(9.2)

Функции   определены для любых значений  . Они предполагаются непрерывными по совокупности переменных   и непрерывно дифференцируемыми по  . Управление u надо выбрать так, чтобы функционал

(9,3)

принимал наименьшее возможное значение.

Обозначим через   функцию, определяемую дифференциальным уравнением

(9,4)

и начальным условием

(9.5)

При этом подлежащий минимизации функционал Q можно представить так:

(9,6)

Пусть помимо основной системы уравнений (1) и уравнения (4), которые можно записать совместно так:

(9.7)

мы имеем еще одну систему уравнений относительно вспомогательных (дополнительно рассматриваемых) переменных  :

(9,8)

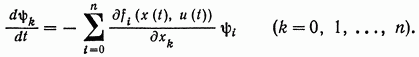(9.9)

Это — система однородных линейных дифференциальных уравнений с переменными коэффициентами. При любых начальных значениях для   она допускает единственное решение

Всякое решение системы уравнений (9) (при любых начальных условиях) будем называть решением системы (8), соответствующим выбранному управлению   и фазовой траектории 

Обозначая

(9.10)

будем иметь

(9.11)

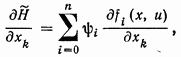(9.12)

и системы уравнений (7) и (8) можно переписать так:

Поставленная выше задача решается при помощи принципа максимума Л. С. Понтрягина, установленного и доказанного [72] в виде сформулированной ниже теоремы.

(9.13)

(9.14)

(9.15)

(9.16)

(9.17)