8. Теорема о пространстве решений однородной системы линейных алгебраических уравнений.

Совокупность Pвсех решенийоднороднойсистемы уравнений являетсялинейным пространством, которое представляет собой подпространство линейного пространства всех вектор-столбцов высотыn.

1).

2).

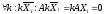
9. Теорема о связи общих решений неоднородной и однородной систем линейных алгебраических уравнений.

Общее решение неоднородной системы линейных уравнений имеет вид

, где Х₀– некоторое (частное) решение неоднородной системы уравнений

- общее решение однородной системы

AX=B

A(X₀+C₁X₁+C₂X₂+…+ C_nX_n)=AX₀+C₁AX₁+…+C_nAX_n=AX₀=B

Множество решений неоднородной системы линейных уравнений не образует линейного пространства.

10. Формулы Крамера для системы двух линейных уравнений с двумя переменными.

(Правило Крамера для системы nxn) – Пусть дана система АХ=В из 2 линейных уравнений с 2 неизвестными. То есть у нас получается системы 2х2.

Если |А|≠0, то системы имеет единственное решение:

, где А₁означает матрицу, полученную из А заменой 1 столбца столбцом В, а А₂получена из А заменой второго столбца столбцом В.

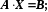
11. Линейная независимость векторов, составляющих ортонормированную систему.

Начнем с определения, что такое ортонормированная система.

Здесь доказывается линейная независимость 3х3

12. Формулы для вычисления координат вектора в ортогональном базисе.

- ортогональный базис

13. Невырожденность ортогональной матрицы.

14. Изменение матрицы линейного преобразования при замене базиса.

А’=T^-1AT

Пусть А – матрица линейного преобразования fв базисе.

Предположим, что мы переходим к новому базису, в котором преобразованию отвечает новая матрица А’, а Т есть матрица перехода от исходного базиса к новому базису.

Х=ТХ^’, где Х – столбец из старых координат разложенного по базису вектора, а Х’ – столбец из новых координат. АналогичноY=TY’

Учитывая, что Y=AX, Х=ТХ^’ иY=TY’, установим связь между Х’ иY’.

Y’=T^-1Y=T^-1AX=T^-1ATX’

Отсюдаследует, что матрицей отображения А в новом базисе будет матрица A’=T^-1ATX, чтд.

15. Равенство характеристических многочленов подобных матриц.

А

В: Р^-1АР

16. Ортогональность собственных векторов, соответствующих различным собственным значениям самосопряженного линейного преобразования.

Будем вести индукцию по n. В случаеn=1 любое преобразование имеет вид

Поэтому любой ненулевой вектор хявляется собственным, и доказывать нечего.

Предположим, что утверждение теоремы верно для симметрических преобразований в евклидовом пространстве размерности n-1, и в этом предположении докажем его для евклидова пространства размерностиn.

Прежде всего возьмем какое-либо собственное значение λ₁симметрического преобразованияf. По теореме о действительности корней уравнения симметрической матрицы λ₁– действительно число. Пустьа₁– соответствующий собственный вектор.

Обозначим через S– множество всех векторов, ортогональных ка₁

Так как подпространствоSесть ортогональное дополнение к линейной оболочкеL(а₁), то его размерность равнаn-1. Покажем, что это подпространство выдерживает действиеf. Это означает, что если, то. Действительно,

Из сказанного следует, что действие fна всем пространствеVможно при желании сузить до действияfна подпространствеS. Применяя предположение индукции, получим, что вSсуществует ортогональный базис, состоящий из собственных векторов преобразования, т.е.

Вместе с равенствомэто доказывает нашу теорему.