
Законы для механической системы
Строго говоря, для описания движения системы из N материальных точек необходимо записать N векторных дифференциальных уравнений, решить их с учётом некоторых начальных условий, проанализировать все решения и сделать суждения. Математически такая задача часто бывает неразрешимой. Поэтому всякий результат (вывод), полученный в отношении движения системы как целого, представляет определённую ценность. Отдельные такие выводы и результаты называются законами движения механической системы. К ним относятся, например, закон изменения импульса, закон сохранения импульса; закон изменения энергии, закон сохранения энергии; закон изменения момента
импульса, закон сохранения момента импульса.
З а к о н и з м е н е н и я и м п у л ь с а.
З а к о н с о х р а н е н и я и м п у л ь с а
Импульсом
системы называется вектор
![]() где mi
, vi ––
масса и скорость i-й материальной
точки системы.
где mi
, vi ––
масса и скорость i-й материальной
точки системы.
В производную dP/dt войдут слагаемые midvi /dt. По закону Ньютона каждое такое слагаемое можно приравнять результирующей внешней силе Fi и результирующей внутренней силе fi со стороны остальных частиц. При суммировании Fi и fi сумма всех внутренних сил будет равна нулю, так как, например, для силы f12 согласно третьему закону Ньютона найдётся равная по модулю и противоположная сила f21 . Получается, что
![]() (12)
(12)
где F –– результирующая всех внешних сил, действующих на систему.
Это и есть закон изменения импульса для механической системы.
Импульс системы можно представить как произведение общей массы m системы на некоторую скорость VC, которую называют скоростью центра масс системы. Формулировка закона изменения импульса в терминах центра масс
![]() (13)
(13)
От закона изменения импульса легко перейти к закону сохранения импульса:
Fi = 0, F = 0, P = const. (14)
Механическая система, на которую не действуют никакие внешние силы, называется замкнутой системой.
В замкнутой механической системе импульс есть величина постоянная.
В терминах центра масс этот закон формулируется так:
Fi = 0, F = 0, VC = const; (15)
Центр масс замкнутой механической системы покоится или движется равномерно и прямолинейно.
З а к о н ы с о х р а н е н и я и и з м е н е н и я э н е р г и и
Рассмотрим сначала простейшую систему, состоящую из одного точечного тела. Запишем закон Ньютона в виде
![]() .
.
Далее уравнение скалярно помножим на перемещение dl = vdt. В результате слева будет величина m(v∙dv) = d(0,5v2) = dEk, Величина Ek = 0,5mv2 была названа кинетической энергией. Справа появится величина
(F∙dl) = Fldl = δA. Эту величину называют элементарной работой силы на отрезке пути dl. В результате такого скалярного умножения получается уравнение
δA = dEk . (16)
Такое же равенство можно записать для неэлементарных величин:
A12 = ∆ Ek = Ek2 - Ek1. (17)
На каком-либо участке траектории работа действующих на тело всех сил равна изменению кинетической энергии тела.
В случае силового поля внешних неподвижных тел работа по перемещению какого-либо пробного тела не зависит от формы пути, а зависит лишь от начального и конечного положений тела. Это позволяет ввести потенциальную энергию тела (наряду с кинетической). Представим себе, например, лёгкое заряженное тело имеет на бесконечном удалении от одноимённо заряженного внешнего массивного тела скорость v и начинает приближаться. По мере приближения пробное тело замедляется и в какой-то момент останавливается. Кинетическая энергия в этот момент равна нулю. Но какой смысл говорить, что движение исчезло, если в следующие моменты тело вновь приобретёт скорость? Резонней говорить о переходе открытой (явной ) формы движения (кинетическая энергия) в некую скрытую форму. Какой же мерой обладает тело в точке остановки по сравнению с кинетической энергией на бесконечном удалении? Такой мерой является возможность совершения работы над телом при перемещении из данного положения в бесконечность (где тело уже не испытывает влияния силового центра). Потенциальной энергией тела в силовом постоянном поле называют запас возможной работы при перемещении тела из данного положения в некоторое нулевое (стандартное) положение. Работу по перемещению тела из положения 1 в положение 2 можно выразить через изменение потенциальной энергии:
A12 = A1∞ - A2∞ = U1 - U2 = -∆ U.
Работа равна убыли потенциальной энергии. Такое силовое поле называется потенциальным, или консервативным, и механическая система будет иметь такое же название.
Для
малого перемещения dl
работу Fldl
можно теперь записать ещё и как
–dU. При dl = dx
будет Fxdx
= – dU, откуда
![]() Аналогично, рассмотрев перемещения
dl = dy, dz, получим
Аналогично, рассмотрев перемещения
dl = dy, dz, получим
![]() .
.
Таким образом, связь между функциями F(x,y,z) и U(x,y,z) оказывается следующей
![]() (18)
(18)
Сила есть взятый со знаком «-» градиент потенциальной энергии.
Введение потенциальной энергии позволяет сформулировать закон сохранения энергии для материальной точки:
![]() (19)
(19)
В консервативных системах полная механическая энергия, равная сумме кинетической и потенциальной энергий, сохраняется.
Эта формулировка подходит и для системы из N материальных точек. В этом случае потенциальная энергия может быть подразделена на потенциальную энергию в поле внешних консервативных сил и потенциальную энергию взаимодействия частиц между собой. Аналогично, кинетическая энергия системы может быть представлена как сумма кинетической энергии движения системы как целого (половина произведения массы всей системы на квадрат скорости центра масс) и кинетической энергии движения частиц относительно центра масс. В случае, если внешнее силовое поле является однородным (как, например, поле силы тяжести), то потенциальную энергию можно записать как энергию тела с массой всей системы и с координатами центра масс.
Закон изменения механической энергии формулируется для случая, когда создающие силовое поле внешние тела движутся в выбранной системе отсчёта. Соответствующее этому силовое поле изменяется со временем. Силы называют сторонними, или неконсервативными. Закон изменения энергии:
![]() (20)
(20)
Изменение полной энергии равно работе сторонних (неконсервативных) сил. К сторонним силам можно отнести и диссипативные силы, действующие внутри системы.
З а к о н и з м е н е н и я м о м е н т а и м п у л ь с а .
З а к о н с о х р а н е н и я м о м е н т а и м п у л ь с а
Возьмём
случай одной материальной точки. Вектор
L = [r,mv]
называется моментом импульса материальной
точки. Производная по времени от
этой величины будет ![]() так как векторное произведение векторов
dr/dt
и v
равно нулю. Множитель mdv/dt
есть сила F, действующая
на материальную точку. Вектор M
= [r,F]
называют вектором момента силы.
Отсюда получается уравнение
так как векторное произведение векторов
dr/dt
и v
равно нулю. Множитель mdv/dt
есть сила F, действующая
на материальную точку. Вектор M
= [r,F]
называют вектором момента силы.
Отсюда получается уравнение
![]() (21)
(21)
О
Рис. 1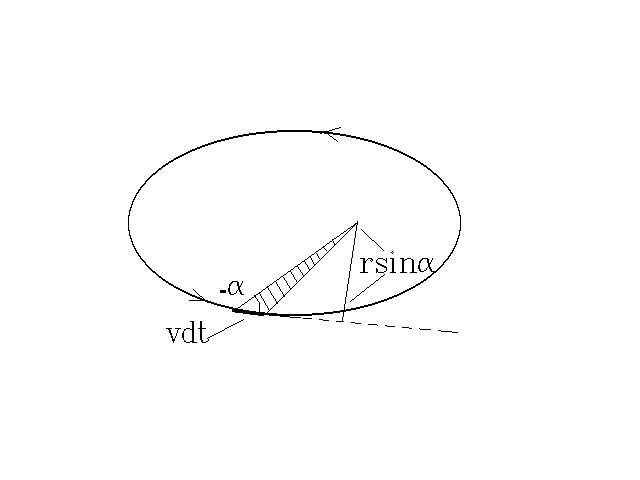
Для замкнутой механической системы
Fi = 0, M = 0, L = const. (22)
То есть в
замкнутой механической системе момент
импульса есть величина постоянная –
закон сохранения момента импульса.
Этот закон нередко используется при
решении задач. Если для конкретной
механической системы удалось заметить,
что при некотором выборе начала отсчёта
момент внешних сил отсутствует или
пренебрежимо мал, то момент импульса
этой системы надо считать постоянным.
Скажем, для системы из двух материальных
точек должно быть m1[r1,v1]
+ m2[r2,v2]
= const. Для материальной точки в
поле действия центральной силы должно
выполняться условие [r,v]
= const, где r –
радиус-вектор материальной точки
относительно силового центра. Последнее
равенство означает постоянство секторной
скорости – площади, “замазываемой”
радиус-вектором за единицу времени. На
рис. 1 видно, что
![]() есть высота заштрихованного треугольника,
а vdt – основание его.
Произведение этих величин есть величина
векторного произведения [r,v]
и вместе с тем это удвоенная площадь,
замазанная радиус-вектором за время
dt.
есть высота заштрихованного треугольника,
а vdt – основание его.
Произведение этих величин есть величина
векторного произведения [r,v]
и вместе с тем это удвоенная площадь,
замазанная радиус-вектором за время
dt.
В р а щ а т е л ь н о е д в и ж е н и е т в ё р д о г о т е л а .
П л о с к о е д в и ж е н и е
Законы сохранения и изменения момента импульса особенно ярко проявляются при плоском движении твёрдого тела. Частным случаем плоского движения является вращательное движение, когда частицы движутся по окружностям разных радиусов, центры которых лежат на одной прямой –– оси вращения. Ниже будут рассмотрены простейшие случаи, иллюстрирующие законы изменения и сохранения момента мпульса, сохранения энергии.
П
Рис. 2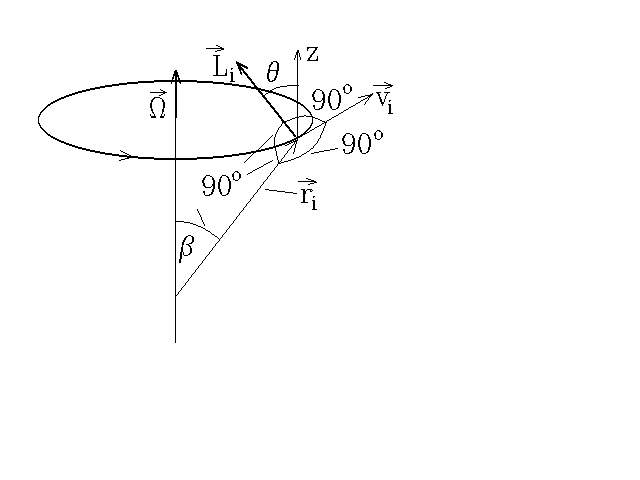
![]() к вектору угловой скорости
к вектору угловой скорости![]() ( рис. 2). При равномерном вращении тела
(
( рис. 2). При равномерном вращении тела
(![]() ) вектор Li
частицы будет описывать конус с углом
2
) вектор Li
частицы будет описывать конус с углом
2![]() при вершине. Неизменной будет проекция
вектора на ось z:
при вершине. Неизменной будет проекция
вектора на ось z: ![]() .
Учитывая, что
.
Учитывая, что
![]() ,
,
для
Lz
получим![]() .
.
Но
![]() есть радиус вращения i-й
частицы. Для проекции момента импульса
всего твёрдого тела получается
есть радиус вращения i-й
частицы. Для проекции момента импульса
всего твёрдого тела получается ![]() .
.
Сумма ![]() называется
моментом инерции твёрдого тела
относительно данной оси вращения. Таким
образом
называется
моментом инерции твёрдого тела
относительно данной оси вращения. Таким
образом
![]() (23).
(23).
При равномерном вращении величина Lz сохраняется. В общем случае согласно уравнению (21) должно быть
dLz/dt = Mz,
то есть равномерное вращение будет при условии Mz = 0 .
Если же момент сил Mz отличен от нуля, то
![]() . (24)
. (24)
Уравнение
(24) называют уравнением динамики
вращательного движения. Все величины
имеют прозрачный смысл. Iz
–– мера инертности при вращательном
движении, Mz
–– мера воздействия на вращающееся
тело,
![]() –– мера “отклика” вращающегося тела
на воздействие. Момент сил относительно
оси вращения Mz
(проекция вектора M
на ось z) обусловлен
касательными силами (силами,
перпендикулярными оси вращения).
–– мера “отклика” вращающегося тела
на воздействие. Момент сил относительно
оси вращения Mz
(проекция вектора M
на ось z) обусловлен
касательными силами (силами,
перпендикулярными оси вращения).
Случай ![]() есть
проявление закона сохранения момента
импульса.
есть
проявление закона сохранения момента
импульса.
Формулу, подобную (23), можно записать и для случая вращения симметричного твёрдого тела вокруг своей оси симметрии:
![]() , (25)
, (25)
где IC –– момент инерции тела относительно оси симметрии, а значит, относительно оси, проходящей через центр масс. Ось симметрии является свободной осью. Тело может вращаться вокруг такой оси, даже если ось не закреплена. В теоретической механике доказывается, что в любом твёрдом теле (произвольной формы) есть три взаимно перпендикулярные свободные оси (главные оси).
При отсутствии момента внешних сил вращающееся вокруг свободной оси тело сохраняет величину угловой скорости и ориентацию оси вращения.
Назовём ещё примеры, иллюстрирующие закон сохранения момента импульса.
1. Свободно вращающееся вокруг главной оси тело в какой-то момент резко меняет момент инерции I1 на I2 . Должно выполняться соотношение
![]() , (26)
, (26)
где
![]() – угловые скорости до и после смены
момента инерции.
– угловые скорости до и после смены
момента инерции.
2. Соосно вращающиеся тела могут взаимодействовать друг с другом при отсутствии моментов внешних сил. Должно выполняться условие
![]() , (27)
, (27)
где i –– номер вращающегося тела.
Кинетическая энергия вращающегося тела.
Произведение
![]() – угол поворота относительно данной
оси, есть элементарная работа силы над
вращающимся телом, а значит, приращение
кинетической энергии тела. Если Mz
заменить его выражением из уравнения
(24), то получится
– угол поворота относительно данной
оси, есть элементарная работа силы над
вращающимся телом, а значит, приращение
кинетической энергии тела. Если Mz
заменить его выражением из уравнения
(24), то получится
![]() .
.
Кинетическая энергия тела, вращающегося вокруг неподвижной оси, будет
![]() . (28)
. (28)
Формула применима и для записи кинетической энергии тела, вращающегося вокруг оси, проходящей через центр масс (не обязательно вокруг главной оси).
Плоское движение твёрдого тела.
При обсуждении кинематики твёрдого тела уже отмечалось, что перемещение любой точки тела можно представить как перемещение центра масс тела и перемещение по дуге некоторого радиуса относительно центра масс. Соответственно работу силы, приложенной в некоторой точке твёрдого тела, можно представить как сумму работы силы на перемещении центра масс и работы на перемещении точки приложения силы относительно центра масс. В соответствии с этим кинетическую энергию плоского движения можно записать в виде
![]() . (29)
. (29)
Формулу (29) можно применить к случаю вращения тела около закреплённой оси. Скорость центра масс можно представить как произведение угловой скорости на расстояние d от центра масс до оси вращения. Тогда получится, что
![]() .
.
С другой стороны, эту же энергию можно записать как
![]() ,
,
где I –– момент инерции тела относительно закреплённой оси вращения. Между моментами инерции IC и I должно быть соотношение
I = IC + md2 . (30)
Соотношение (30) выражает теорему Штейнера: Момент инерции относительно некоторой оси вращения равен сумме момента инерции относительно оси, проходящей через центр масс и параллельной данной, и произведения массы тела на квадрат расстояния между осями.
Рис. 3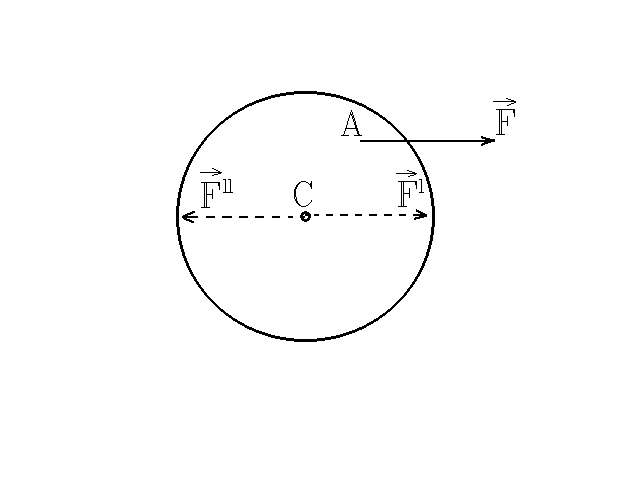
M = Fl, где l –– расстояние между линиями действия сил пары (плечо пары). Второе уравнение динамики плоского движения:
![]() . (31)
. (31)
Таким образом, динамика плоского движени твёрдого тела выражается уравнениями (13) и (31).
МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
К и н е м а т и к а к о л е б а т е л ь н о г о д в и ж е н и я
Колебательные движения –– это движения, повторяющиеся во времени. Простейшей периодической функцией является гармоническая функция cos или sin. Простейшим колебанием является гармоническое колебание, когда в формуле для координаты время входит под знак косинуса или синуса:
![]() . (32)
. (32)
Правую
часть (32) можно истолковать как проекцию
на ось x вектора длиной A,
вращающегося в плоскости xy
с угловой скоростью
![]() .
Начальный угол наклона этого вектора
к оси x –
.
Начальный угол наклона этого вектора
к оси x –
![]() .
Поэтому
.
Поэтому
![]() называют циклической частотой
колебаний. Величины A и
называют циклической частотой
колебаний. Величины A и
![]() называют соответственно амплитудой
и начальной фазой колебания, величину
называют соответственно амплитудой
и начальной фазой колебания, величину
![]() – фазой колебания. Изображение
упомянутого вектора называют векторной
диаграммой колебания.
– фазой колебания. Изображение
упомянутого вектора называют векторной
диаграммой колебания.
Сложение колебаний одного направления
Бывают случаи, когда смещение x
материальной точки представляет собой
сумму смещений x1
+ x2
+ …, каждое из которых есть
гармоническое колебание :![]() .
.
Выяснение
того, как выглядит сумма x1
+ x2
+ …, как её проще и п
Рис. 4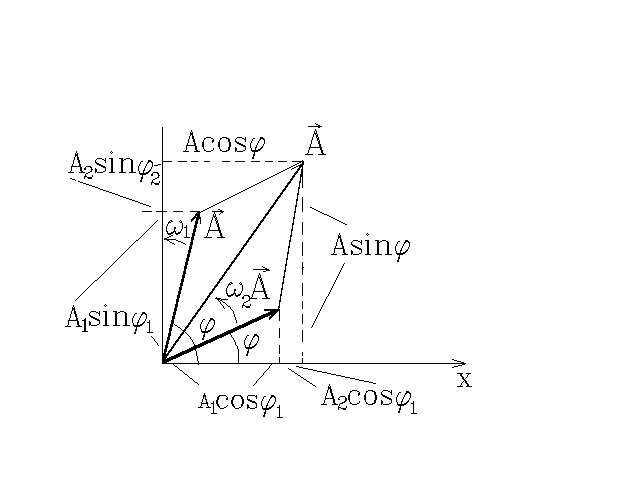
![]() .
. ![]() . (33)
. (33)
![]() . (34)
. (34)
Если
частоты исходных колебаний одинаковы,
то разность фаз
![]() можно заменить разностью начальных
фаз
можно заменить разностью начальных
фаз
![]() .
.
Теперь на
вопрос, как записать кинематическое
уравнение гармонического колебания,
можно ответить двояко: или как одно
колебание с амплитудой A и
некоторой начальной фазой
![]() ,
или как сумму двух колебаний с
амплитудами a и b
,
или как сумму двух колебаний с
амплитудами a и b
![]() ,
причём A2
= a2
+b2
,
,
причём A2
= a2
+b2
, ![]() .
.
На основании уравнения гармонических колебаний (32) скорость и ускорение материальной точки запишутся следующим образом:
![]() , (35)
, (35) ![]() . (36)
. (36)
Амплитуда
скорости Av
есть произведение амплитуды A
на частоту
![]() .
Ускорение пропорционально смещению x
со знаком минус и коэффициент
пропорциональности есть квадрат
частоты.
.
Ускорение пропорционально смещению x
со знаком минус и коэффициент
пропорциональности есть квадрат
частоты.
Д и н а м и к а к о л е б а н и я
На основании формулы (36) сила, под действием которой точечное тело совершает гармонические колебания, есть сила типа
F = – Cx, (37)
где C можно представить как произведение массы и квадрата частоты:
![]() . (38)
. (38)
Такую силу называют квазиупругой. Уравнение
Рис. 5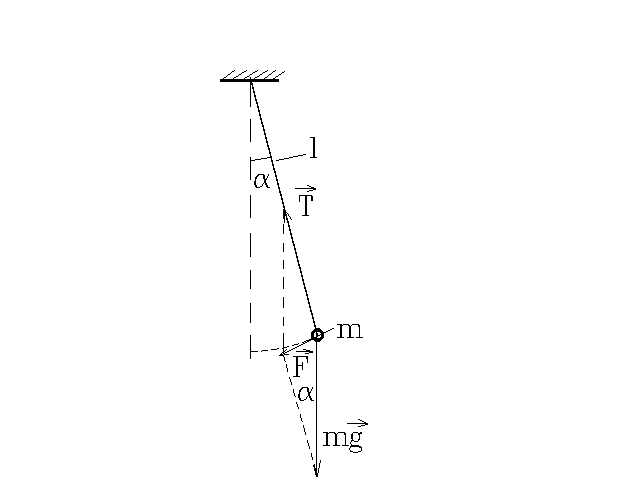
![]() (39)
(39)
е
Рис. 6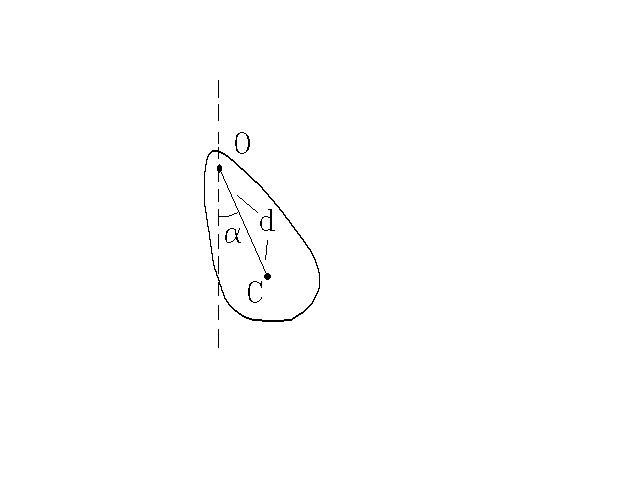
Примером квазиупругой силы является сила пружины
F = - kx, где k –– жёсткость пружины, показывающая
силу пружины
при её единичном удлинении (или
сокращении). Если на закреплённой с
одного конца пружине находится груз
массой m, то он будет
колебаться с частотой
![]() .
.
Ещё примером
квазиупругой силы является результирующая
сил, действующих на точечный груз,
подвешенный на нити, отклонённой на
малый угол от вертикали (математический
маятник). Эта результирующая может быть
записана как
![]() ( рис. 5). Знак "–" учитывает то, что
сила направлена в сторону уменьшения
угла отклонения. При малых углах
отклонения смещение можно считать
прямым отрезком x и, кроме
того,
( рис. 5). Знак "–" учитывает то, что
сила направлена в сторону уменьшения
угла отклонения. При малых углах
отклонения смещение можно считать
прямым отрезком x и, кроме
того,
![]() .
И тогда получается F=–(mg/l)x.
В роли коэффициента C
здесь выступает mg/l . Для
частоты и периода имеем (формулы
Гюйгенса)
.
И тогда получается F=–(mg/l)x.
В роли коэффициента C
здесь выступает mg/l . Для
частоты и периода имеем (формулы
Гюйгенса)
![]() . (40)
. (40)
Следующий пример – физический маятник. Им называется тело, способное вращаться вокруг оси, проходящей выше центра масс тела ( рис. 6). Уравнению динамики вращательного движения можно придать вид
![]()
где I
–– момент инерции относительно оси
O;
![]() – соответственно угловое ускорение
и плечо силы тяжести; точка С – центр
масс.
– соответственно угловое ускорение
и плечо силы тяжести; точка С – центр
масс.
При малых углах отклонения это уравнение есть уравнение типа (39). В роли x выступает угол, в роли массы – I, в роли коэффициента C – множитель mgd. Поэтому для частоты и периода будут справедливы формулы::
![]() (41)
(41)
Формулам (41) можно придать тот же вид, что и формулам Гюйгенса, если величину I/md, имеющую размерность длины, обозначить далее через lпр. Величину lпр называют приведённой длиной физического маятника:
![]() . (41l)
. (41l)
Энергия гармонического колебания
Энергия гармонического колебания
складывается из кинетической энергии
0,5mv2
и потенциальной энергии в поле
квазиупругой силы 0,5Cx2.
Подставляя явные выражения (32), (35) для
x и v и учитывая, что
![]() ,
получаем
,
получаем
![]() . (42)
. (42)
То есть полную энергию (постоянную) можно записать как сумму отдельно кинетической и отдельно потенциальной энергий, или как максимальную кинетическую энергию, или как максимальную потенциальную энергию. . Следует заметить, что для гармонического колебания среднее значение (за период) кинетической энергии равно среднему значению потенциальной энергии.
З а т у х а ю щ и е к о л е б а н и я
Реальная колебательная система часто находится в среде, и на колеблещуюся материальную точку действует сила сопротивления. Начальная энергия тела постепенно уменьшается. В этом случае, как говорят, система совершает затухающие колебания. Особенности затухания колебаний можно выяснить с помощью уравнения динамики, составленного с учётом силы сопротивления среды. Последнюю при малых скоростях движения записывают
как Fr = - rv = - rdv/dt где r – постоянная, называемая коэффициентом сопротивления (его трудно спутать с расстоянием, так как в последующих формулах речь идёт только о функции смещения x(t) ) . Уравнение динамики теперь имеет вид
![]() . (43)
. (43)
Функция x(t), удовлетворяющая данному дифференциальному соотношению (43), будет такой :
![]() (44)
(44)
где
