2 Образец выполнения расчётно - графической работы

Задание 1.а Вычислите площадь плоской фигуры, ограниченной линиями, которые заданы уравнениями:

2х² – 4х + у = 0, 2х – у – 4 = 0. Сделайте чертёж.

Решение. 1) Для вычисления площади заданной фигуры сначала построим её.

Первая линия, определяемая уравнением 2х²–4х+у=0 или у = 4х – 2х², является параболой, заданной трёхчленным уравнением вида у = ах² + bх +с, ось симметрии которой параллельна оси Оy. Так как коэффициент

a = -2< 0, то ветви параболы направлены вниз.

Координаты вершина параболы находятся по формулам : ,

у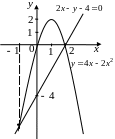 = у( x₀ )=y (1)=4 – 2=2.Следовательно, вершина находится в точке с координатами (1; 2).

Найдём точки пересечения параболы с осями координат.

С осью Ox: у = 0  4х – 2х² = 0  2х(2 - х) = 0 

 х₁ = 0; х₂ = 2;

с осью Oy: х = 0  у = 0.

Строим параболу (рисунок 6).

Вторая линия, определяемая уравнением

2х – у – 4 = 0 – прямая.

Для построения прямой найдем её точки пересечения

с осями координат: .

Строим прямую (рисунок 6). Заштрихованная область, Рисунок 6 заключенная между параболой и прямой, и есть фигура, площадь которой требуется найти.

2) Заштрихованная область не является криволинейной трапецией, поэтому необходимо спроектировать её на ту из осей координат, где при этом получится один отрезок. Для этого необходимо из точек пересечения линий опустить перпендикуляры на оси координат.

Определим поэтому точки пересечения линий, ограничивающих заштрихованную фигуру. Для этого решаем систему, составленную из уравнений заданных линий:

. Таким образом, имеем две точки пересечения линий: (2;0), (-1;-6).

3) Из рисунка 6 видно, что при проектировании области на ось Ох получаем один отрезок [-1; 2], на котором парабола находится «выше» прямой, то есть выполняется соотношение f₂(х)= 4х – 2х² ≥ f₁(х)= 2х – 4. Тогда для вычисления площади применяем формулу (4): или

(кв. ед.).

Замечание: если область проектировать на ось Oy, то мы получили бы два отрезка: [-6;0] и [0;2], а тогда находить площадь области было бы сложнее. В других задачах, возможно, что проектирование на ось Oy приведёт к противоположной ситуации.

З адание 1.б Вычислите объём тела, образованного вращением вокруг оси Оу плоской фигуры, ограниченной графиками функций: у = х³,

у² = х. Сделайте чертёж.

Решение. 1) Построим фигуру, ограниченную

заданными линиями: у = х³ – кубическая парабола,

у² = х – парабола, а затем тело вращения (рису-

нок 7).

2) Найдем точки пересечения линий,

ограничивающих заштрихованную фигуру:

Рисунок 7

. Имеем две точки:

(0;0), (1;1)

3) Так как заштрихованная область вращается вокруг оси Oy, то проектируем её на эту ось. Кубическая парабола находится «правее» параболы на отрезке [0; 1] по оси Оу, т.е. (рисунок 7).Тогда объём тела вращения вокруг оси Оу найдём по формуле:

, где , с ≤ у ≤ d

(куб. ед.)

Задание 2.а Вычислите несобственный интеграл (или установите его расходимость) : .

Решение. Мы имеем несобственный интеграл с бесконечным нижним пределом, тогда по определению:

.