32

М инистерство сельского хозяйства Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

« НОВОЧЕРКАССКАЯ ГОСУДАРСТВЕННАЯ МЕЛИОРАТИВНАЯ КАДЕМИЯ»

Кафедра математики

ОПРЕДЕЛЁННЫЕ ИНТЕГРАЛЫ И ИХ

ПРИЛОЖЕНИЯ

Методические указания

к выполнению расчётно-графической работы

(для студентов всех направлений)

Новочеркасск

2012

Министерство сельского хозяйства Российской Федерации

Ф едеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

« НОВОЧЕРКАССКАЯ ГОСУДАРСТВЕННАЯ МЕЛИОРАТИВНАЯ КАДЕМИЯ»

Кафедра математики

ОПРЕДЕЛЁННЫЕ ИНТЕГРАЛЫ И ИХ

ПРИЛОЖЕНИЯ

Методические указания

Новочеркасск

2012

У ДК 517.38

Р 598

Методические указания составлены зав. каф. математики, канд. техн. наук Рогозиной Ю.С. и доцентом каф. математики Кузнецовой М.В.

Рецензенты: Дьяченко В.Б., канд. техн. наук, профессор, зав. каф. информатики ФГБОУ ВПО НГМА

Башняк И.М., канд.техн. наук, доц. каф. математики ФГБОУ ВПО НГМА

Рогозина, Ю.С.

Р 598 Определённые интегралы и их приложения: [Текст]: метод. указ. к выполнению расчётно-графической работы для студ. всех направлений / Ю.С. Рогозина, М.В. Кузнецова; Новочерк. гос. мелиор. акад., каф. мат-ки - Новочеркасск, 2012. – 31с.

Методические указания предназначены студентам I курса очной формы обучения всех направлений НГМА для организации их самостоятельной работы при выполнении расчётно-графической работы по теме «Определённые интегралы и их приложения» в курсах дисциплин: «Математика», «Высшая математика», «Математический анализ».

Ключевые слова: определённый интеграл, площадь, объём тела вращения, несобственные интегралы, численное интегрирование.

Оглавление

с

1 КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ……………………………….4

1. Геометрические приложения определённого интеграла………………4

2. Вычисление несобственных интегралов (или установление их расходимости)……………………………………………………………6

3. Численные методы вычисления определённого интеграла…………...7

2 ОБРАЗЕЦ ВЫПОЛНЕНИЯ РАСЧЁТНО-ГРАФИЧЕСКОЙ РАБОТЫ.....12

3 ВАРИАНТЫ ЗАДАНИЙ ДЛЯ ВЫПОЛНЕНИЯ РАСЧЁТНО-

ГРАФИЧЕСКОЙ РАБОТЫ………………………………………………...21

ПРИЛОЖЕНИЕ. Контрольные вопросы для защиты РГР…..……………..29

ЛИТЕРАТУРА ………………………………….…………………………….30

Данное пособие предназначено для студентов I курсов всех направлений при выполнении ими расчётно-графической работы (РГР) по теме: «Определённые интегралы и их приложения».

Расчётно-графическая работа содержит 3 задания:

1. Геометрические приложения определённого интеграла:

а) вычисление площадей плоских фигур;

б) вычисление объёмов тел вращения.

2. Вычисление несобственных интегралов (или установление их расходимости).

3. Численные методы вычисления определённого интеграла.

При выполнении третьего задания предполагается один из примеров решать с применением пакета Mathcad на персональном компьютере.

Перед выполнением РГР необходимо изучить теоретический материал, используя литературу [1-4], а также конспекты лекций.

При решении задач требуется обосновывать каждый этап решения, исходя из теоретических положений курса. Вычисления следует располагать в строгом порядке, отделяя вспомогательные вычисления от основных.

Чертежи можно выполнять от руки, но на миллиметровой бумаге, аккуратно и в соответствии с данными условиями, указывая оси, масштаб.

При защите РГР необходимо уметь отвечать на контрольные вопросы, которые приведены в приложении.

1 Краткие теоретические сведения

1.1 Геометрические приложения определённого интеграла

а) вычисление площадей плоских фигур

Исходя из геометрического смысла определенного интеграла, площадь фигуры, ограниченной графиком непрерывной функции у = f(х) (f(х) ≥ 0), двумя прямыми х = а и х = b, параллельными оси Оу и отрезком [а; b] оси Ох, или площадь криволинейной трапеции (рисунок 1,а), вычисляется по формуле: (1)

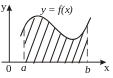
а) б) в)

Рисунок 1

Если f(х) ≤ 0 на отрезке [а; b] (рисунок 1,б), то площадь фигуры, ограниченной дугой графика у = f(х), а ≤ х ≤ b вычисляется по формуле:

(2)

В случае, когда фигура ограничена графиком непрерывной функции х = φ(у), (φ(у) ≥ 0), двумя прямыми х = с, х = d, параллельными оси Ох и отрезком [с; d] оси Оу (рисунок 1, в), её площадь вычисляется по формуле:

(3)

Площадь фигуры, ограниченной графиками непрерывных функций у=f₁(х) и у=f₂(х), причем f₁(х) ≤ f₂(х) на отрезке [а; b], и двумя прямыми х= а, х =b (рисунок 2, а), вычисляется по формуле: (4)

а) б) в)

Рисунок 2

Аналогично, площадь фигуры, изображённой на рисунке 2, б, вычисляется по формуле: (5)

Для фигуры, изображенной на рисунке 2, в, площадь следует определять как сумму площадей S₁ и S₂, для каждой из которых применяем формулу (1):

(6)

б) вычисление объёмов тел вращения

Если криволинейная трапеция, ограниченная кривой у = f(х), а ≤ х ≤ b, вращается вокруг оси Ох (рисунок 3, а), то объём тела вращения вычисляется по формуле: (7)

а) б) в)

Рисунок 3

Аналогично, при вращении криволинейной трапеции ограниченной кривой х = φ(у), с ≤ у ≤ d, вокруг оси Оу (рисунок 3, б), объём тела вращения вычисляется по формуле: (8)

Если фигура, ограниченная графиками непрерывных функций у=f₁(х) и у=f₂(х), f₁(х) ≤ f₂(х) на отрезке [а; b], и двумя прямыми х= а, х =b (рисунок 3, в), вращается вокруг оси Ох, то объём тела вращения вычисляется по формуле: (9)