5. Ціла і дробова частина числа α

Цілою частиною дійсного числа α називається найбільше ціле число, яке не перевищує α, тобто таке ціле число п, що . Позначається [α]. Значить, .

Дробовою частиною дійсного числа α називається різниця . Позначається {α}. Значить, {α}= і .

Приклад. [5,8]=5, [ ]=3, [-7,39]=-8, [-e]=-3, { }=0,1415…, { }= .

Теорема 3. Нехай α – дійсне додатне число, d – ціле додатне. Кількість додатних чисел, що не перевищують α і діляться на d, дорівнює .

Доведення. Розглянемо додатні числа, кратні d і які не перевищують . Нехай найбільше з них дорівнює sd, так що (s+1)d вже більше, ніж α. Кількість таких чисел d, 2d, 3d,…, sd дорівнює s, де , значить, , тобто .

Теорема 4. Для будь-якого дійсного числа α>0 і цілого d>0 .

Доведення. Між [α] і α немає цілих чисел, і тому кількість чисел, кратних d. В сегменті 1, [α], яка рівна згідно теореми 3 , рівна також величині , яка виражає кількість чисел, кратних d, в сегменті 1, α.

Теорема 5. Для будь-якого дійсного числа α різниця може бути рівна тільки 0 або 1.

Доведення. Для будь-якого α маємо: , так що , , тобто ціле число може бути рівним лише 0 або 1.

Теорема 6. Нехай р – просте число, – ціле. Для показника α найвищого степеня р, який ділить п!, маємо: , (1) тобто при α, рівному сумі (1), п! тотожно ділиться на р^α, але п! тотожно не ділиться на р^α+1.

Зауваження: ряд (1) є скінченим, бо, якщо в знаменнику появляється степінь p^s, більший чисельника п, то доданки (1) перетворюються в нулі.

Доведення.

При n<p всі доданки в ряді (1) рівні 0, і разом з тим дійсно в цьому випадку показник найвищого степеня р (який ділить п!), рівний 0. так що для таких р і п твердження теореми вірне.

Візьмемо тепер довільне просте число р і застосуємо метод індукції по п.

При п=1 теорема вірна, бо п=1<p.

Допустимо, що твердження теореми вірне для всіх п. таких що , де і ціле. Доведемо для n=N.

Якщо N<p, то твердження теореми вірне для N ( із ).

Якщо , то серед множників 1, 2, …, N добутку N! Число тих, які діляться на р, буде рівне (теорема 3). Добуток всіх решти множників числа позначимо через М. Тоді , (2), де M тотожно не ділиться на р. Із випливає . А для всіх (1) виконується. Так що згідно припущенню показник найвищого степеня р, який ділить !, рівний 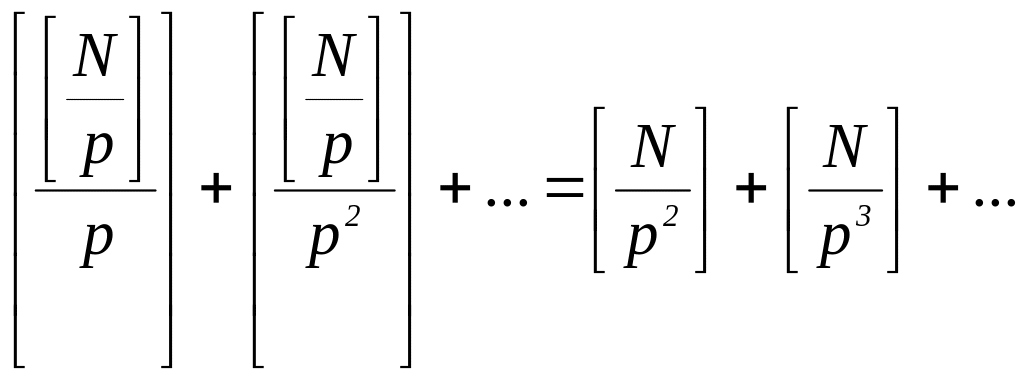(3) (теорема 4). Із формули (2) одержуємо, що найбільший показник степеня р, який ділить N!, рівний .

Таким чином, твердження теореми вірне для N і в цьому випадку. Отже, теорема при довільному простому р вірна для будь-якого натурального числа п.

Приклад. Знайти найбільше α, таке що 1000! .

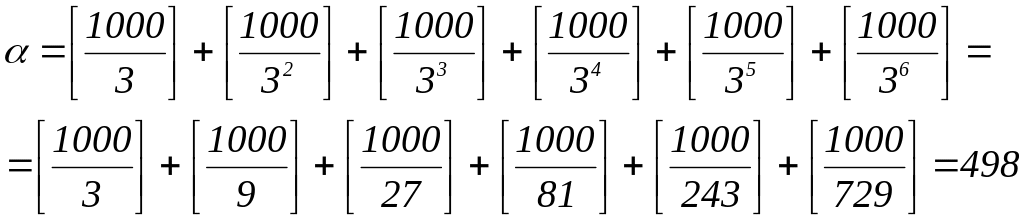
Теорема 6 дає можливість знаходити канонічний розклад п!, а саме, оскільки кожне просте число р входить в канонічний розклад п! з показником, рівним ..., то .

6. Основні числові функції

Через позначають числову функцію, значення якої для будь-якого натурального n дорівнює числу всіх його натуральних дільників.

Через позначають числову функцію, значення якої для будь-якого натурального n дорівнює сумі всіх його натуральних дільників.

Теорема 6. Нехай – канонічний розклад на прості множники натурального числа n. Тоді число натуральних дільників числа n визначається формулою .

Доведення: Відомо, що будь-який натуральний дільник d числа n має вигляд: , де (1). Тому, щоб знайти число всіх натуральних дільників числа n, достатньо підрахувати число все можливих упорядкованих наборів , які задовольняють умови (1). Згідно цих умов, може приймати значень. Вибори різних значень не залежать один від одного і в силу єдності розкладу на прості множники різним наборам відповідають різні дільники числа n. Отже, число всіх натуральних дільників числа n дорівнює добутку .

Приклад.

1) n=60. n=2²∙3∙5. .

2) n=12. ,

.

Через позначають числову функцію, значення якої для будь-якого натурального числа n дорівнює числу натуральних чисел, взаємно простих з n, які не перевищують n. Функцію називають функцією Ейлера.

Наведемо основні властивості функції Ейлера.

1.

2. Сума значень функції Ейлера для всіх дільників числа n дорівнює n. – формула Гаусса.

Приклад.

n=12. Дільники: 1, 2, 3, 4, 6, 10.