Лекція 3 Прості і складені числа

1. Поняття простого і складеного числа

Означення. Натуральне число p називається простим, якщо воно ділиться тільки на самого себе і на одиницю. Натуральне число a, яке, крім 1 і а, має і інші дільники, називається складеним. Число 1 не належить ні до простих, ні до складених чисел.

Отже, кожне натуральне число є або просте, або складене або дорівнює 1.

Властивості простих чисел:

1. Якщо просте число р ділиться на деяке натуральне число 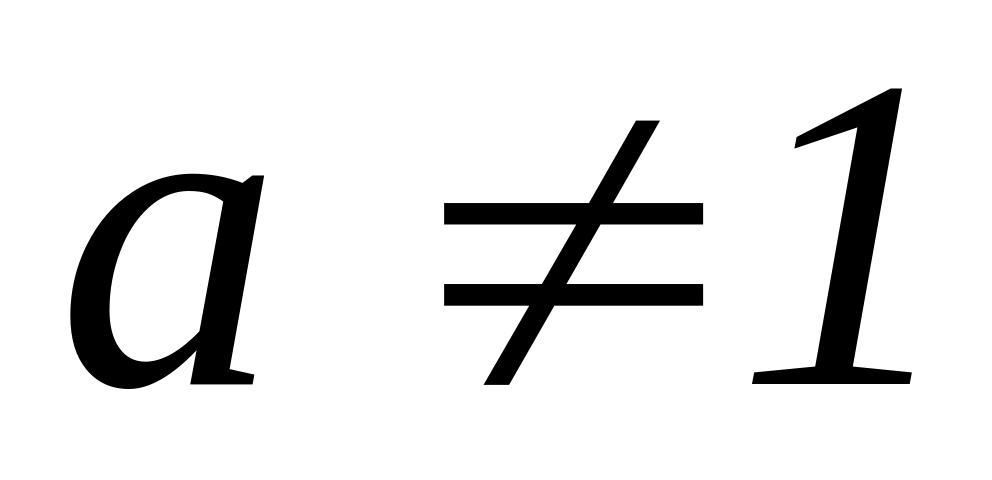, то р=а.

Дійсно, якщо , то р матиме хоча б три дільники а, р, 1 і не буде простим.

2. Кожне натуральне число а або ділиться на просте число р, або з ним взаємно просте.

Дійсно, (а, р) як дільник р може дорівнювати або 1, або р. У першому випадку а і р взаємно прості, в другому – а ділиться на р.

3. Добуток двох ( або кількох) натуральних чисел ділиться на просте число р тоді і тільки тоді, коли принаймні один із співмножників ділиться на р.

Дійсно, це випливає із властивості 1. Якщо і ( b, c)=1, то .

4. Найменший (відмінний від одиниці) дільник натурального числа a>1 є число просте.

Дійсно, нехай q – найменший дільник натурального числа a>1, тобто a=a₁q. Якби q було складене. То q=q₁q₂, де q₁<q і q₂<q. Тоді a=a₁q₁q₂=(a₁q₁)q₂=(a₁q₂)q₁. Це показує, що а має дільниками числа q₁ і q₂, які менші за q, що суперечить припущенню.

5. Найменший простий дільник складеного числа а не більший .

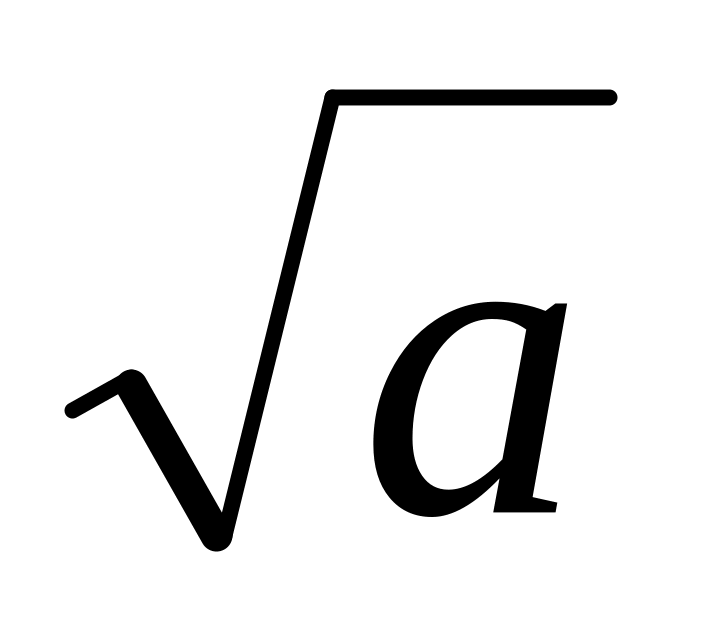Дійсно, нехай q – цей дільник, тоді a=a₁q, . Перемноживши ці два записи, маємо . Скоротимо на a₁. одержимо: , тобто .

Ця властивість може бути критерієм того, чи є дане число простим чи складеним, тобто якщо натуральне число а не ділиться на жодне просте число , то воно просте.

2. Основна теорема арифметики

Теорема 1. Кожне натуральне число a>1 можна подати у вигляді добутку простих чисел і до того ж тільки єдиним способом ( якщо не братии до уваги порядок розміщення співмножників).

Доведення. Справді, нехай a>1 – натуральнее число, р₁ – його найменший простий дільник. Тоді а=р₁а₁.

а) Якщо а₁=1, то а – просте і теорема доведена.

б) Якщо a₁>1, то, позначаючи буквою р₂ його найменший простий дільник, одержимо: а₁=р₂а₂. Якщо a₂>1, то аналогічно а₂=р₃а₃, і продовжуємо цей процесс доти, поки не дійдемо до рівності a_n-1=p_n, де p_n – просте число. Це мусить колись статися, бо числа a, a₁, a₂,…, a_k,… утворюють спадну послідовність натуральних чисел (згідно принципу найменшого числа). Отже, деяке a_n буде дорівнювати 1, а a_n-1=p_n буде простим числом. Запишемо все послідовно: а=р₁а₁, а₁=р₂а₂, а₂=р₃а₃,…, а_n-2=р_n-1а_n-1, a_n-1=p_n. Перемножимо ці рівності і скоротимо: a=p₁p₂p₃…p_n [3.1] ( n ). Ми одержали розклад числа а на прості множники.

Доведемо єдність такого розкладу. Від супротивного. Нехай a=q₁q₂…q_s

( s ) – ще один такий розклад. Тоді p₁p₂…p_n= q₁q₂…q_s. Права частина тотожно ділиться на q₁, отже ( за властивістю 3) принаймні один співмножник лівої частини тотожно ділиться на q₁. оскільки нумерація – довільна, нехай , але тоді ( за властивістю 1) p₁= q₁. скоротимо обидві частини на q₁.

p₂p₃…p_n= q₂q₃…q_s. Повторюючи попередні міркування, одержимо:

p₃p₄…p_n= q₃q₄…q_s. І так далі, поки в одній частині не скоротяться всі співмножники ( якщо , то у правій). Але одночасно мусять скоротитися і всі співмножники лівої частини, бо рівність p_n-sp_n-s+1…p_n=1 можлива лише при p_n-s =p_n-s+1 =…=p_n=1. Отже, другий розклад на прості множники збігається з першим. І теорему доведено.