Раздел і. Статика

Глава 1. Введение в статику

1.1. Основные понятия статики

Статика – раздел механики, изучающий способы приведения сложных систем к более простым эквивалентным им, а также условия равновесия тел под действием различных систем сил.

В теоретической механике рассматриваются не конкретные тела, а их следующие идеализированные модели:

- материальная точка – тело, размерами которого в данных условиях можно пренебречь (например, Земля в ее движении вокруг Солнца). Материальная точка имеет массу и способность взаимодействовать с другими телами;

- механическая система – совокупность материальных точек, положения и движения которых взаимосвязаны;

- абсолютно твердое тело – система материальных точек, расстояние между которыми всегда остается неизменным;

- сплошная среда – система материальных точек, расстояние между которыми может изменяться.

В ажнейшим понятием теоретической механики является понятие силы. Сила – мера механического воздействия одного тела на другое, определяющая направление и интенсивность данного действия. Взаимодействие тел может происходить как при их непосредственном контакте, так и с помощью силовых полей различной природы (например электрического или магнитного). Все физические величины делятся на скалярные и векторные. Сила – векторная величина, ее основные характеристики: п-п - линия действия и А – точка приложения (рис. 1.1).

Рис. 1.1. – Основные характеристики силы

В системе СИ единицей измерения силы является ньютон (Н), реже используют техническую систему единиц МКГСС и систему СГС. В них единицей измерения силы являются килограмм-сила (1 кгс = 9,81 Н) и дина (1 дин = 10^-5 Н) соответственно.

В теоретической механике вычисления часто проводятся с помощью расчетных схем. Расчетная схема – реальный объект, освобожденный от несущественных особенностей. На рис. 1.2 а, сделанном Галилеем, показан реальный объект, а на рис. 1.2, б – его расчетная схема.

Рис. 1.2. – Реальный объект и его расчетная схема

Все силы по характеру воздействия на тело делятся на два типа:

- сосредоточенные – силы, которые можно считать приложенными в одной точке (рис. 1.2, б), такие силы характеризуются абсолютным значением. На самом деле через тело, не имеющее размеров, невозможно передать силовое воздействие, поэтому такая сила является схематизацией действительности;

- распределенные – силы, которые нельзя считать приложенными в одной точке. Они характеризуются интенсивностью и бывают трех видов:

- - распределенные по поверхности p (рис. 1.3, б) – силы, приложенные в месте контакта тел, когда площадью контакта нельзя пренебречь. Интенсивность измеряется в Н/м², примером могут служить сила действия ветра и снеговая нагрузка, давление газа на стенки цилиндра двигателя и поршень.

- - линейно распределенные q (рис. 1.3, в) - силы, которые могут быть приведены к оси тела, например сила действия поезда на железнодорожные рельсы.

- - распределенные по объему γ (рис. 1,3, а) – силы, не являющиеся результатом контакта тел. Они приложены в каждой точке объема, занятого телом. Примером является силы инерции, собственный вес тела, архимедова сила.

Рис. 1.3. – Виды распределенных сил

Система сил – совокупность сил, действующих на тело. Геометрически системы сил классифицируются следующим образом:

- сходящиеся – линии действия сил пересекаются в одной точке;

- параллельные – линии действия сил параллельны;

- произвольные – линии действия сил не параллельны и не пересекаются.

По расположению в пространстве системы сил делятся на:

- плоские – линии действия сил лежат в одной плоскости;

- пространственные – линии действия сил не лежат в одной плоскости.

По направлению действия силы делятся на:

- внешние – действуют со стороны точек или тел, не входящих в данную систему;

- внутренние – силы взаимодействия между материальными точками данной системы. Принадлежность силы к тому или иному типу определяется рассматриваемой системой, поэтому одна сила может быть как внешней, так и внутренней.

По характеру действия системы сил бывают:

- эквивалентные – под действием каждой из них тело находится в одном и том же состоянии;

- уравновешенные - системы, не меняющие состояния тела, к которому они приложены.

1.2. Связи и их реакции

В теоретической механике все точки и системы материальных точек делятся на свободные (на их движение не наложены ограничения) и несвободные. Свободная материальная точка имеет три степени свободы, свободная система материальных точек – шесть. Если система несвободна, то говорят, что на ее перемещение наложенные связи.

Связь – тело или поле, ограничивающее перемещение рассматриваемой материальной точки или твердого тела. Также существуют связи, накладываемые на скорость и ускорение точки или тела, то есть ограничивающие движение в целом.

Р еакция связи – сила, с которой связь действует на рассматриваемую материальную точку или твердое тело. Реакции связей называют пассивными силами, поскольку они возникают только под действием активных (внешних) сил. На рис. 1.4 активная сила G (вес самолета) вызывает появление трех пассивных сил R₁, R₂ и R₃ в местах контакта его колес со связью (взлетной полосой).

Рис. 1.4. – Связи и их реакции

В статике рассматриваются простейшие связи, выполненные в форме различных твердых или гибких тел.

В шарнирно подвижной опоре реакция перпендикулярна поверхности качения (рис. 1.5, а), а в шарнирно неподвижной реакцию находят по горизонтальной и вертикальной составляющим (рис. 1.5, б). Реакция невесомой нерастяжимой нити (троса, шнура или цепи) всегда направлена по нити к точке закрепления (рис. 1.5, в). Реакцию сферического шарнира (подпятника) определяют через три взаимно перпендикулярные составляющие по правилу параллелепипеда (рис. 1.5, г).

Рис. 1.5. – Наиболее распространены связи и их реакции

В случае идеально гладкой поверхности точка контакта тела А свободно скользит по ней, поэтому существует только нормальная реакция N_A. Если поверхность шероховатая (рис. 1.6, а), то к нормальной реакции добавляется горизонтальная реакция связи – сила трения F_A. В случае защемления в озникают три силовых фактора (рис. 1.6, б) – вертикальная и горизонтальная реакции и крутящий момент, который будет подробно рассмотрен в следующем параграфе.

Рис. 1.6. – Реакции шероховатой поверхности и защемления

1.3. Аксиомы статики

В основе статики лежит шесть аксиом, установленных опытным путем и длительными наблюдениями за физическими явлениями реального мира.

Аксиома I (об уравновешенной системе)

Д ве силы являются уравновешенной (эквивалентной нулю) системой, если они лежат на одной прямой, равны по величине и противоположны по направлению (рис. 1.7). Эта аксиома справедлива только для абсолютно твердого тела.

Рис. 1.7. – Уравновешена система сил

Аксиома IІ (аксиома инерции)

Под действием уравновешенной системы сил материальная точка (тело) движется равномерно и прямолинейно или находится в состоянии покоя. Эта аксиома часто называется законом инерции Галилея.

Аксиома IІI (о параллелограмме сил)

Р авнодействующая системы сил R – сила, эквивалентная заданной системе сил. В случае двух сил, приложенных к телу в одной точке, равнодействующая равна их векторной сумме и приложена в той же точке (рис. 1.8). Графически равнодействующая определяется по правилу параллелограмма, а ее модуль находится по формуле

(1.1)

Рис. 1.8. – Параллелограмм сил

Из данной аксиомы следует, что геометрически можно складывать любое количество сил, приложенных в одной точке. Для этого к концу первого вектора прикладывают начало второго, к концу второго – начало третьего и т.д. Соединив начало первого вектора с концом последнего, получаем равнодействующую сил (рис. 1.9). Полученная фигура называется силовым многоугольником. Если же начало первого вектора совпадет с концом последнего (замкнутый многоугольник), то равнодействующая системы равна нулю.

У равновешивающая – сила, равная по модулю равнодействующей и направленная по линии ее действия в противоположную сторону.

Рис. 1.9. – Силовой многоугольник

Аксиома IV (о наложении новых связей)

Равновесие твердого тела не нарушится при наложении на него дополнительных связей.

Аксиома V (об освобождении от связей)

Несвободное твердое тело можно представить свободным, на которое кроме внешних сил действуют реакции связей.

П усть шар лежит на гладкой горизонтальной плоскости, которая является связью (рис. 1.10, а). Из этой аксиомы следует, что шар можно представить свободным, находящимся под действием внешней силы тяжести G и равной по величине, но противоположной по направлению реакции связи N (рис. 1.10, б).

Рис. 1.10. – Принцип освобождения от связей

Аксиома VI (о затвердении)

Равновесие деформируемого тела сохранится, если не изменяя его формы, размеров и положения в пространстве, представить его абсолютно твердым. Эта аксиома позволяет решать простые задачи статики гибких тел (расчет нитей, цепных и ременных передач), применив к ним методы статики твердого тела.

1.4. Простейшие теоремы статики

Т еорема о трех силах: если абсолютно твердое тело находится в равновесии под действием трех непараллельных сил и линии действия двух сил пересекаются, то все силы лежат в одной плоскости и их линии действия пересекаются в одной точке.

Доказательство. Переносим в точку В пересечения линий действия силы F₁ и F₂ и складываем их (рис. 1.11)

Рис. 1.11. – Теорема о трех силах

Теперь на тело действуют две силы – R и F₃. Чтобы тело находилось в равновесии, они должны образовывать уравновешенную систему. Это означает, что их линия действия тоже проходит через точку А.

Уравновешена система из трех сил является замкнутым треугольником. Зная три элемента этого треугольника (сторону и два прилегающие углы или две стороны и угол между ними), можно определить другие неизвестные элементы: силы или углы между силами.

Т еорема о силе как скользящем векторе: действие силы на твердое тело не изменится, если перенести ее в пределах тела по линии действия в любую точку.

Доказательство. Пусть в точке А к телу приложена сила F. В произвольной точке В на ее линии действия приложим уравновешенную систему сил F и - F (рис. 1.12).

Согласно аксиомы І, сила F в точке А и -F в точке В образуют уравновешенную систему, эквивалентную нулю. В результате остается только сила F, приложенная в точке В. Из этого следует, что сила скользящим вектором.

Рис. 1.12. – Теорема о силе как скользящем векторе

1.5. Условия равновесия системы сходящихся сил

Все сходящиеся силы могут быть перенесены в точку пересечения их линий действия А. Две силы складываются по правилу параллелограмма (рис. 1.6), а для сложения большего числа сил используют силовой многоугольник (рис. 1.7). В случае трех сходящихся сил, образующих пространственную систему, пользуются правилом параллелепипеда.

Равнодействующую системы сил можно определить и аналитически: любую силу можно разложить на составляющие по координатными осями

,

где i, j, k – единичные векторы (орты). Тогда равнодействующая системы сходящихся сил равна векторной (геометрической) сумме слагаемых

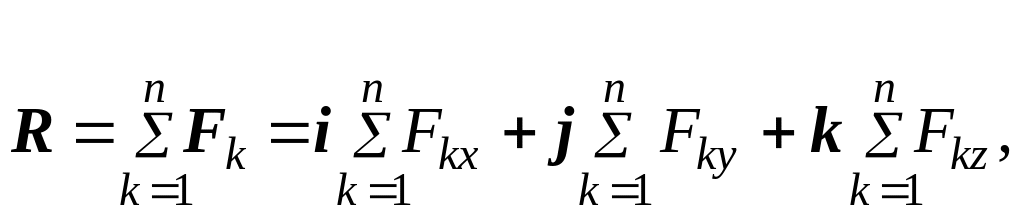(1.2)

где F_kx, F_ky і F_kz – проекции соответствующих сил на координатные оси.

Модуль равнодействующей определяется по формуле

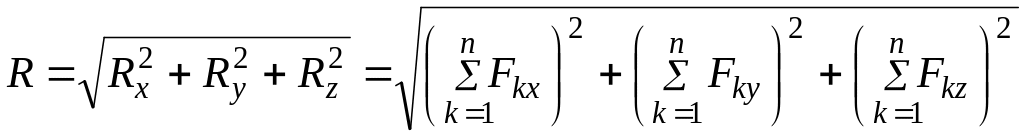. (1.3)

Углы между направлением равнодействующей и координатными осями находятся при помощи направляющих косинусов

. (1.4)

Необходимым и достаточным условием равновесия тела под действием системы сходящихся сил является равенство нулю равнодействующей данной системы, то есть

(1.5)

Векторному уравнению (1.5) соответствуют следующие скалярные выражения

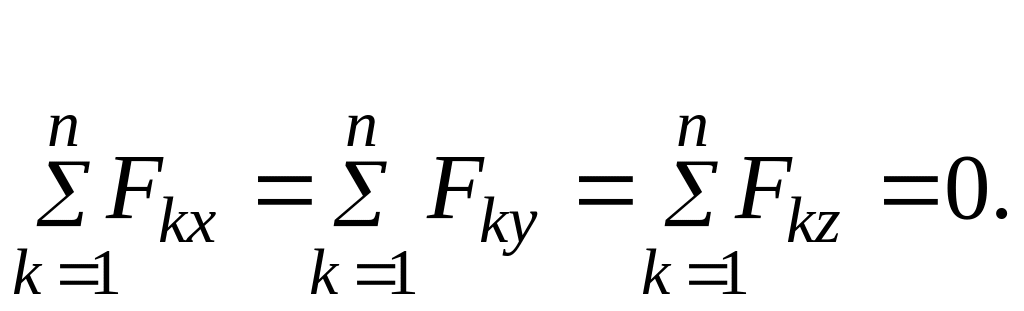или (1.6)

Формулы (1.6) являются аналитической формой условия равновесия системы сходящихся сил: для равновесия произвольной системы сходящихся сил необходимо и достаточно, чтобы алгебраические суммы проекций сил на три взаимно перпендикулярные оси равны нулю.

В случае плоской системы сходящихся сил для условия равновесия получаем следующие уравнения

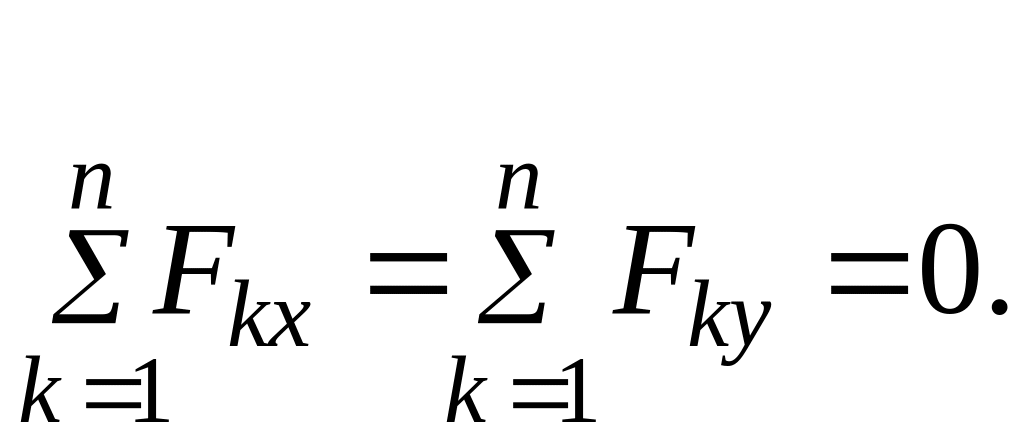или (1.7)