Раздел іі. Кинематика

Глава 7. Кинематика точки

7.1. Общие определения кинематики

Кинематика – раздел теоретической механики, в котором движение абсолютно твердого тела или материальной точки изучается независимо от действующих на них сил. Пространство, в котором происходит движение, считается трехмерным, а все измерения выполняются по законам евклидовой геометрии.

Движение – изменение положения тела или точки в пространстве с течением времени. Для определения движения тела или точки необходимо иметь систему отсчета.

Система отсчета – часы и тело отсчета, относительно которого рассматривается движение данного тела. Могут быть как подвижными, так и условно неподвижными. Движение тела или точки напрямую зависит от выбора системы отсчета. Все системы отсчета принято подразделять на два типа:

- инерциальные – в них изолирована материально точка может бесконечно долго находиться в состоянии покоя или равномерного и прямолинейного движения. Всегда находятся в состоянии покоя или движутся равномерно и прямолинейно.

- неинерциальные – не имеют свойств предыдущих систем.

Если в каждый момент времени можно определить положение тела относительно системы отсчета, то движение считается заданным (задан закон движения).

Траектория – линия, которую описывает тело или точка в процессе движения. По форме может быть прямолинейная или криволинейная.

Основная задача кинематики: нахождение способов задания и определение общих кинематических характеристик: положения тела, его скорости и ускорения.

7.2. Способы задания движения материальной точки, уравнения движения

Существует три способа задания движения материальной точки: векторный, координатный и естественный.

7.2.1. Векторный способ

Положение точки в пространстве однозначно определяется радиус-вектором r, проведенным из некоторого неподвижного центра О в данную точку М (рис. 7.1). В процессе движения точки радиус-вектор изменяется по величине и направлению, а уравнения движения точки в векторной форме имеет вид

r = r(t). (7.1)

Годограф – линия, образованная концами какого-либо вектора при его движении. Поэтому, траектория точки М является годографом ее радиус-вектора.

Рис. 7.1. – Векторный способ задания движения

Векторный способ задания движения очень удобен для вычислений, поэтому широко применяется в кинематике и динамике.

7.2.2. Координатный способ

П оложение точки М в декартовой системе отсчета Oxyz описывается посредством задания трех координат x, y и z (рис. 7.2). Уравнения движения точки в декартовых координатах

x = х(t), y = у(t), z = z(t). (7.2)

Движение точки в плоскости описывается двумя первыми уравнениями, если же точка движется прямолинейно, то достаточно одного уравнения.

Рис. 7.2. – Задание движения в декартовой системе координат

Если выразить с первого уравнения время

t = φ(x)

и подставить в два последних уравнения, то получается

y = y(x), z = z(x) (7.3)

уравнение траектории точки в декартовых координатах.

П оложение точки М в полярной системе отсчета задается через две координаты r и φ (рис. 7.3). Тогда уравнение движения точки

r = r(t), φ = φ(t). (7.4)

Если выразить из второго уравнения время и подставить в первое уравнение, то получаем

r = r(φ) (7.5)

уравнение траектории точки в полярных координатах.

Рис. 7.3. – Задание движения в полярной системе координат

Переход от декартовых координат к полярным и наоборот проводится по формулам

Положение точки М в цилиндрических координатах описывается заданием трех координат r, φ и z (рис. 7.4). Тогда уравнение движения точки

r = r(t), φ = φ(t), z = z(t). (7.6)

Если выразить из первого уравнения время и подставить во второе уравнение, то получится

φ = φ(r), z = z(r) (7.7)

уравнение траектории точки в цилиндрических координатах.

Рис. 7.4. – Задание движения в цилиндрических координатах

Переход от декартовых координат к цилиндрическим проводится по формулам

П оложение точки М в сферических координатах описывается тремя координатами r, ψ и θ (рис. 7.5). Тогда уравнение движения точки

r = r(t), ψ = ψ(t), θ = θ(t). (7.8)

Если выразить из первого уравнения выразить время и подставить во второе уравнение, то получится

ψ = ψ(r), θ = θ(r) (7.9)

уравнение траектории точки в сферических координатах.

Рис. 7.5. – Задание движения в сферических координатах

Переход от декартовых координат к сферическим и обратно производится по формулам

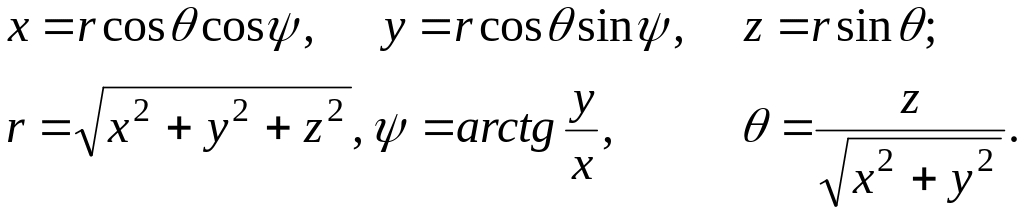(7.10)

7.2.3. Естественный способ

Е сли траектория точки задана заранее, то для определения закона ее движения достаточно указать положение точки на данной траектории. Для этого надо определить начало отсчета О, указать положительное и отрицательное направления. Тогда положение точки М будет определяться только дуговой координатой s, отложенной по траектории от точки О (рис. 7.6).

Рис. 7.6. – Задание движения при естественном способе

Уравнения движения точки в естественном виде

s = f(t), (7.11)

причем эта функция должна быть непрерывной и дифференцируемой.

Дуговую координату s не следует путать с путем σ, пройденным данной точкой. Они равны друг другу только в случае, когда точка М начала движение из центра О в положительном направлении. Если же в начальный момент времени точка занимала положение М₀, а в конечный – положение М и двигалась в одном направлении, то ее путь определяется по формуле

.

7.3. Скорость и ускорение точки при разных способах задания движения

7.3.1. Векторный способ

Мгновенная скорость материальной точки – физическая величина, характеризующая ее перемещение за достаточно малый промежуток и в данный момент времени, равная первой производной радиус-вектора точки по времени:

(7.12)

Скорость направлена по касательной к траектории в сторону движения точки. В случае криволинейной траектории направление вектора скорости непрерывно меняется.

За единицу измерения скорости в системе СИ принят метр в секунду (м/с), также скорость может выражаться в километрах в час (км/ч)

Средняя скорость точки за промежуток времени Δt определяется по формуле

(7.13)

Средняя скорость лишь приближенно отражает характер реального движения точки или тела.

Ускорение материальной точки – характеризует изменение скорости точки, равно первой производной от скорости по времени или второй производной от радиус-вектора по времени

(7.14)

За единицу измерения ускорения в СИ принят метр за секунду в квадрате (м/с²). Поскольку ускорение точки равно первой производной скорости, то оно направлено по касательной к годографу скорости.

Также используется среднее ускорение тела

(7.15)

направленное по вектору Δυ, также достаточно приближенно описывающее характер изменения скорости.

7.3.2. Координатный способ

Проекции скорости точки на неподвижные оси декартовой системы координат равны первым производным соответствующих координат по времени

(7.16)

Вектор скорости точки можно записать через орты

Модуль скорости определяется по формуле

Его направление определяют при помощи направляющих косинусов

Проекции ускорения точки на декартовы оси координат равны первым производным соответствующих проекций скорости по времени на те же оси, или вторым производным соответствующих координат данной точки по времени:

Модуль и направление ускорения определяется по формулам

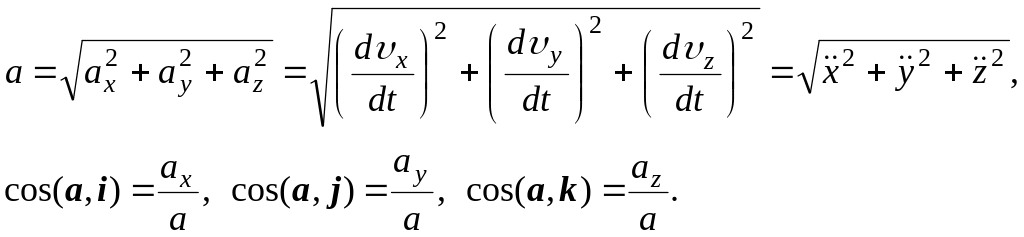
Проекции скорости точки на неподвижные оси полярной системы координат равны первым производным соответствующих координат по времени: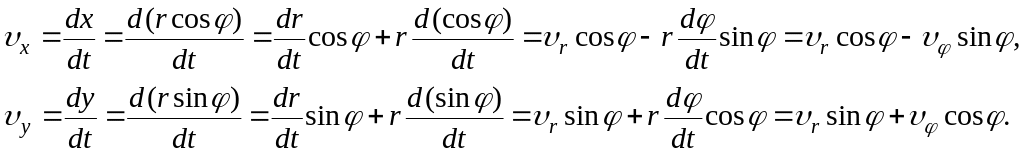

Здесь υ_r і υ_φ – проекции скорости на радиальное и трансверсальное направления соответственно (рис. 7.8).

Модуль вектора скорости в полярных координатах

Проекции ускорения точки на полярные оси координат равны:

Модуль ускорения определяется по формуле

7.3.3. Естественный способ

Каждой точке траектории соответствует определенный радиус-вектор, поэтому при данном способе задания движения для вектора скорости имеем

(7.17)

где τ – орт, который указывающий положительное направление движения.

Модуль скорости равен абсолютному значению производной от дуговой координаты точки по времени

Теорема: полное ускорение точки при естественном способе задания движения равно векторной сумме касательного (тангенциального) и нормального (центростремительного) ускорений

(7.18)

Нормальное ускорение направлено в сторону вогнутости траектории к центру кривизны. Оно характеризует изменение скорости по направлению, а его модуль равен

(7.19)

Нормальное ускорение существует только при криволинейном движении точки.

Касательное ускорение направлено в сторону движения точки по касательной к траектории. Оно характеризует изменение скорости по величине, его модуль равен второй производной от дуговой координаты по времени или первой производной от проекции скорости на касательную по времени

(7.20)

Поскольку касательная всегда перпендикулярна к радиусу, то модуль полного ускорения точки и его направление определяются по теореме Пифагора

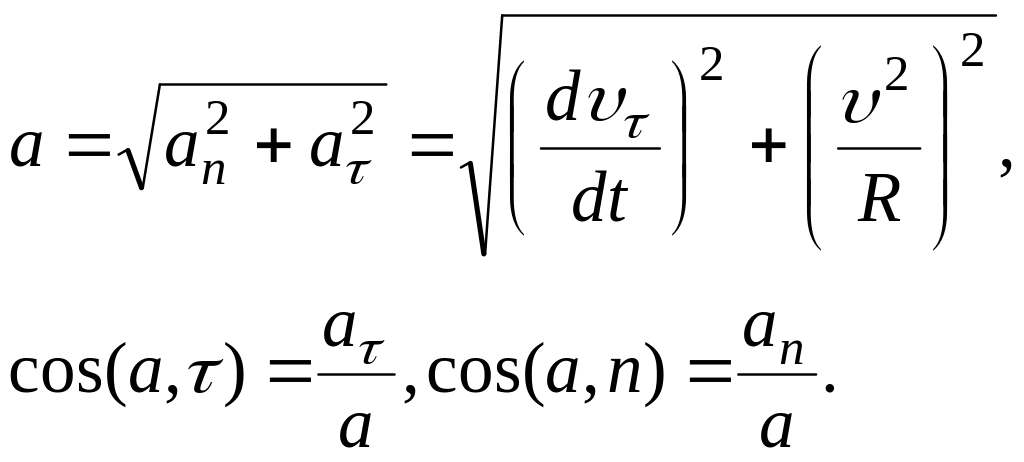(7.21)

Если движение точки задано координатным способом, то уравнение движения точки по траектории имеет вид

(7.22)