Способы формирования ррсч.

1. Метод средних квадратов.

Пусть есть

Получим

и возьмём

2. Мультипликативный способ.

В качестве а – берут число близкое к

x₀ – любое нечётное число < m

// в коспекте дримика есть фраза « m влияет на период » но ее не было в элетронном варианте//

с подбирают экспериментально, оно влияет на корреляцию.

// в конспекте дримика этой фразы нету - (при с=0 - линейный мультиплексированный метод (Лемера)).

30) Равномерность

Проверка по гистограмме с использованием косвенных признаков.

Оценка равномерности м.б. осуществимо либо по гистограмме, либо по

Косвенным критериям.

По гистограмме: определяют диапазон варьирования, который разбивают на N участков, для каждого определяют вероятность и част-ть (хз чо, не осилил смысл слова)

Проверка по косвенным признакам

При косвенном вся последовательность разбивается на пары чисел,

Если интрепритировать как координаты точек, то выполняется условие – точка попадает в круг радиусом 1 вписаного в единичный квадрат.

Геометрически это означает, что точка

Расположена внутри четверти круга

Если числа распределены равномерно, то они должны заполнить квадрат.

Важными характеристиками ПСРРЧ (псевдо-случайные) является длина периода Р и длина отрезка апериодичности L

ВпределахL числа не повторяются.

1. Запускается датчик(ГСЧ) с x₀ и генерируются числа до числа x_r ( x_r попадает на период)

2. Запуск датчика(ГСЧ) с x₀ и фиксируется i₁ и i₂ таких, что x_i=x_r и x_j=x_r. Период Р=j-i

3. Запуск ГСЧ с x₀ и фиксируется x_i = x_i + p

Отрезак апериодичности

Методы увеличения длинны периода:

1.) увеличение глубины рекурсии

Естественно, это ведёт к увеличению затрат машинного времени.

2.)Можно использовать метод возмущений

т.е. если i не кратно М, то Ф, если кратно, ψ.

3.) Макларен-Марсалия.

Основан на использовании 2 датчиков (ГСЧ). Создается вспомогательный массив длинной k (массив V)

D1 дает последовательность {a}; D2 ---//--- {b}; выходная последовательность {c}

1. Vi = ai (i=1-k)

2. Обращение ко 2-му датчику. Получаем b1. С помощью b1 определяется номер S в массиве [b1 k].

3. C1 = Vs

4. Vs = и т.д.

31. Оценка стохастичности и независимости последовательности РРСЧ.

2) Стахостичность

а) метод комбинаций

Вероятность появления j единиц в l разрядах двоичного числа x_i определяется биноминальным законом:

где: - вероятность 1 или 0 в разряде;

Тогда теоретически число чисел с j единицами в l разрядах из N чисел:

Собрав данные по различным по критериям согласия делается вывод о стохастичности.

б) метод серий

Разбивается вся последовательность на элементы 1-го и 2-го рода.

В результате получаем последовательность: а а b b a b b b b a a …

серия

Теоретическая вероятность серии длиной j в последовательности длиной l определяется формулой Бернули:

Получают теоретические и экспериментальные и по критериям согласия делают вывод. (имеет смысл проводить исследование при разных p и l).

3) Независимость – на основе вычисления корреляционного момента.

В общем случае корреляционный момент случайных величин ξ и η с значениями x_i и y_j

где Р_ij – вероятность того, что (ξ, η) принимает значение (x_i, y_j)

При независимости

Коэфициент корреляции

Вводим в рассмотрение 2 последовательности {x_i} и {y_i}={x_i+τ}

Если есть последовательность длиной N, то с вероятностью β можно утверждать, что числа некоррелярны, если выполнить это условие:

31. Метод обратной функции для моделирования последовательности чисел с заданной функцией распределения.

1. Метод обратной функции.

Если случайная величина ξ имеет функцию распределения F(x), то распределение случайной величины y=F_ξ(ξ) равномерно в интервале от 0 до 1.

Пусть η – равномерно распределена от о до 1. Введём случайное число [1], где φ – монотонна. Тогда .

Функция распределения для ξ :

[2]

Из [1]:

Отсюда: т.к. η- равномерна от 0 до 1

[3]

Получим

Отсюда:

Вывод: функция φ, связывающая равномерно распределённую величину η с величиной ξ, имеющую функцию распределения F_ξ есть функция , т.е. обратная по отношению к F_ξ.

31. Универсальный метод моделирования последовательности чисел с заданной функцией распределения.

Разобъём [c,d] на n интервалов

Интервалы выбираются так, чтобы вероятность попадания в любой из них была постоянной:

1) Генерируется РРСЧ из диапазона (0,1) η₁ и выбирается номер диапазона k из условия:

k < n∙η₁ ≤ k+1, k=0…n-1.

2) Генерируется РРСЧ η₂ (от 0 до 1). Формируется случайная величина

= a_k + (a_k+1- a_k) η₂

31. Моделирование последовательности чисел с заданной функцией распределения по гистограмме.

f(x) задана в виде гистограммы

Р – частота

Построим шкалу:

где

Алгоритм:

1) Генерация (РРСЧ из диапазона от 0 до 1).

2) Определяем интервал , на который попала .

3) Генерируем (РРСЧ из диапазона от 0 до 1).

4) Формируем .

31. Нормальное распределение. Формирование случайных чисел с использованием предельных теорем.

Нормальный закон.

Сумма случайных чисел, имеющих один и тот же закон распределения, матожидание m, дисперсию D, среднеквадратичное отклонение σ, подчиняется нормальному закону распределения с матожиданием Nm, с D = ND, и σ = σ, где N – кол-во слагаемых в сумме.

Если в качестве базовой последовательности используют РРСЧ из интервала (0,1), то можно воспользоваться соотношением:

Если в=1, а=0, то

- РРСЧ

Для заданных m и σ.

31. Формирование случайных чисел с использованием теоремы Пуассона. Метод Кана.

Распределение Пуассона.

- вероятность того, что случайная величина примет

значение m (n=0,1)

a) Теорема Пуассона:

Если производится N независимых испытаний и вероятность события А в каждом опыте равна р, то частота появления m событий в N испытаниях при сходится по вероятности к Р_m. При этом Np=λ .

Алгоритм:

Выбираем достаточно большое N , чтобы .

Производятся серии по N испытаний, в каждом из которых проверяют условие:

( -РРСЧ из (0,1))

Подсчитывают количество y_i наступления такого события.

Значения y_i будут распределены по закону Пуассона.

На практике N берут таким, чтобы .

б) Метод Кана

Образуется произведение РРСЧ до выполнения условия:

числа x_j=N_j-1 будут распределены по закону Пуассона.

37. Метод исключения (отбраковки) для моделирования последовательности чисел c заданной функцией распределения.

Метод исключений (отбраковки, режекции, Неймана)

1) Если множество случайных точек (x,y) – реализация случайного вектора , равномерно распределенного в области, ограниченной осью Y и кривой f(x), такой, что

,

то одномерная плотность распределения величины ξ равна

Отсюда следует, что, если f(x) – искомая функция плотности распределения (т.е. ), то, реализовав процедуру построения множества случайных векторов, равномерно распределенных под графиком f(x), мы, тем самым, получим множество значений абсцисс {x_i}, распределённых в соответствии с законом, определяем f(x).

Вместе с тем, процедура генерирования случайных векторов может оказаться достаточно сложной в вычислительном плане (надо использовать условные ф.п.в.). Для упрощения процедуры формирования случайных чисел воспользуемся следующим достаточно очевидным утверждением.

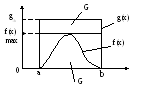
Если мн-во точек (x,y) равномерно распределено под графиком функции g(x) то та часть, что окажется в области под графиком f(x), такой что f(x) <= g(x), тоже будет расп. в области f(x).

Ф-я g(x) называется мажорирующей по отношению к f(х).

g(x)- мажорирующая функция

Можно выбрать функцию g(x) такой, что вектора, равномерно распределенные в области G, будет просто генирировать. Удобно выбирать функцию, имеющую постоянное значение на всей области определения f(x) (как правило, равное) или ступенчатую.

Отсюда вытекает процедура метода:

1) если функция g(x) не ограничена, то, учитывая допустимую погрешность, область ее определения ограничивают интервалом (a,b);

2. генерируется число РРСЧ из диапазона (0, 1) – η1 и преобразуем его в диапазоне (а,b)

η_1* = a+(b-a) η₁ .

2. генерируется число η2 и преобразовывается

η_2* = fmax η₂

2. производим проверку

η_2* < f(η_1*)

Если условие выполняется, то в выходную последовательность записывается число η_1*

х_i= η_1*

_{Если нет, то процедура повторится.}

.

38. Моделирование случайных векторов.

Формирование случайных векторов

с заданными вероятностными характеристиками

Случайный вектор можно задать проекциями на оси координат. Эти проекции являются случайными величинами, описываемыми совместным законом распределения.

В простейшем случае вектор двумерный и может быть задан совместным законом распределения его проекций ξ и η на оси OX и OY.

Рассмотрим способы формирования случайных векторов для моделирования

дискретных и непрерывных случайных процессов

1. Дискретный случайный процесс.

Составляющая ξ принимает значения x₁, x₂, … , x_m, а составляющая η – значения y₁, y₂, … , y_n и каждой паре (x_i y_j) соответствует вероятность P_ij. Совместную функцию распределения вероятностей зададим в виде матрицы

P = .

Тогда каждому возможному значению x_i случайной величины ξ будут соответствовать

В соответствии с этим распределением вероятностей можно определить конкретное значение ξ и из всех значений P_ij можно выбрать последовательность

P_i1, P_i2, … , P_i3, Преобразуем её

.

Эта последовательность списывает условное распределение величины η при условии, что ξ = x_i.

Используя известные нам методы (например, универсальный), определяем конкретное значение y_i1 случайной величины η. Получена первая реализация (x_i1 y_i1)

Вектора. Процедуру повторяем циклически.

2. Непрерывный случайный процесс.

В этом случае двумерная случайная величина (ξ,η) описывается совместной функцией плотности распределения f_ξη (x,y). Напомним,

.

Зная закон распределения системы двух случайных величин, можно определить закон распределения одной из них

.

Имея этот закон, можно сформировать случайное число x_i, а затем при условии, что ξ = x_i определить условное распределение случайной величины η:

.

В соответствии с этой плотностью, можно определить случайное число y_i и получить реализацию вектора (x_i,y_i).

Аналогичным образом можно моделировать случайные вектора и большей размерности. Например, если вектор трехмерный и задан совместной функцией плотности f_ξηζ (x,y,z), то последовательность такова:

,

,

38. Моделирование случайных событий.

Определим наступление события Ri как выполнение условия

Пусть надо реализовать случайное событие А, наступающее с вероятностью р. Будем определять его как выполнение условия

Сложные события - события зависящие от нескольких простых.

Простые А и В и вероятности Р_А, Р_В.

Варианты:

1) А и В независимы

группа исходов:

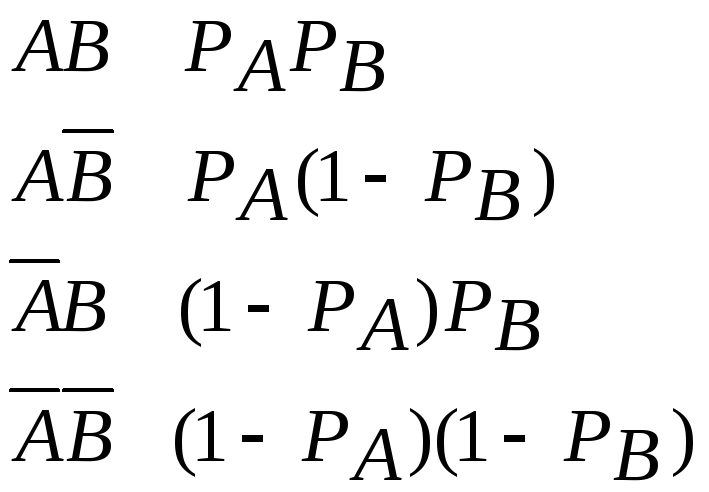
Моделирование их осуществляется либо с помощью 1 случ числа, либо с двумя.

(ниже в лелином конспе не было)

Реализация – либо с последовательными проверками одного числа (СРРЧ)

Либо с двумя случайными числами

Второй вариант с точки зрения удобства построения модели алгоритма, экономия памяти и быстродействие предпочтительнее.

2) А и В зависимы. Должны быть заданы Р_А, Р_В и Р(В/А)

< P_A а) да

б) нет

(етого не было) вычислим