Розділ III. Вступ до математичного аналізу

3.1. Основні означення

Числовою послідовністю називають послідовність чисел кожному із яких присвоєно певний номер, і розташованих у порядку зростання номерів.

Числа називають границею числової послідовності якщо для будь – якого, як завгодно малого наперед заданого існує номер такий, що для всіх виконується нерівність і позначають:

Якщо кожному значенню змінної з деякої області відповідає одне і тільки одне значення величини з деякої області , то зміну називають функцією від змінної і записують:

Сукупність значень , для яких функція існує називають областю визначення функції.

Число називають границею функції при прямуючому до , якщо для будь – якого як завгодно малого існує таке, що як тільки виконується нерівність то виконується і нерівність і позначають:

Змінну називають нескінченно малою при або , якщо виконується нерівність або .

Функцією називають нескінченно великою величиною при , якщо для всіх , які достатньо мало відрізняються від , відповідні значення функції за абсолютною величиною переважають будь – яке наперед задане як завгодно велике додатнє число:

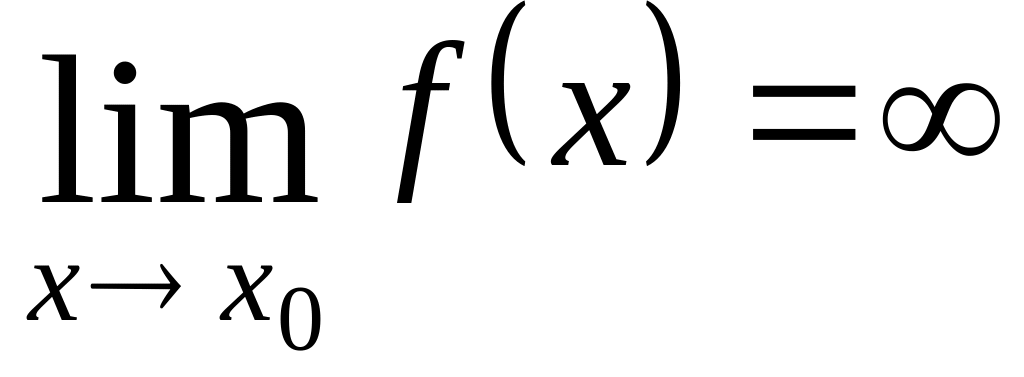
Якщо залишаючись весь час меншим , то пишуть і границю називають границею зліва функції в точці якщо ж і , то записують і границю називають границею справа функції в точці .

Для того щоб існувала границя функції при , необхідно і достатньо, щоб існували границі функції в точці зліва і справа і щоб ці границі були рівні між собою.

3.2 ВЛАСТИВОСТІ ФУНКЦІЇ, ЯКІ МАЮТЬ ГРАНИЦІ.

Якщо існують границі і , то

1. ;

2. 

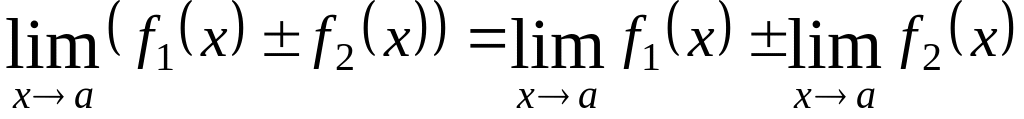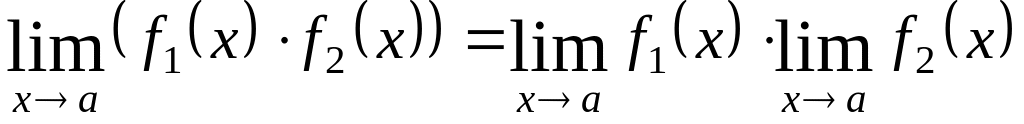
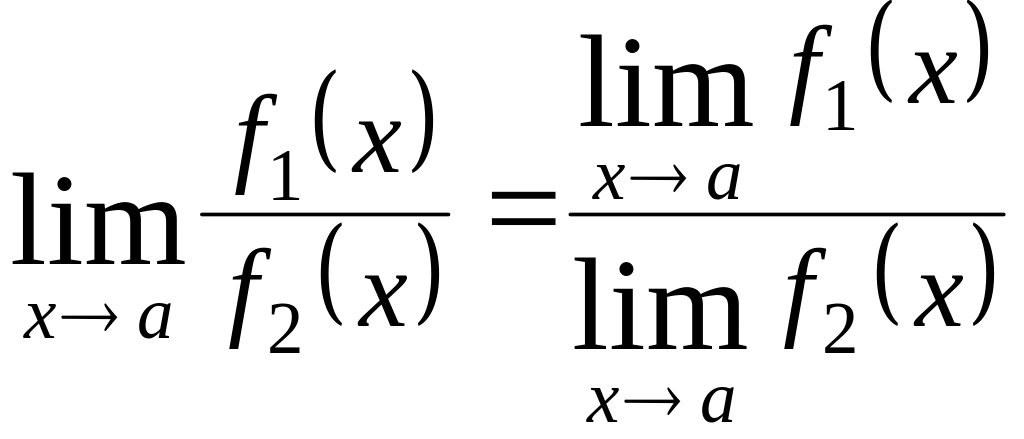3. , якщо

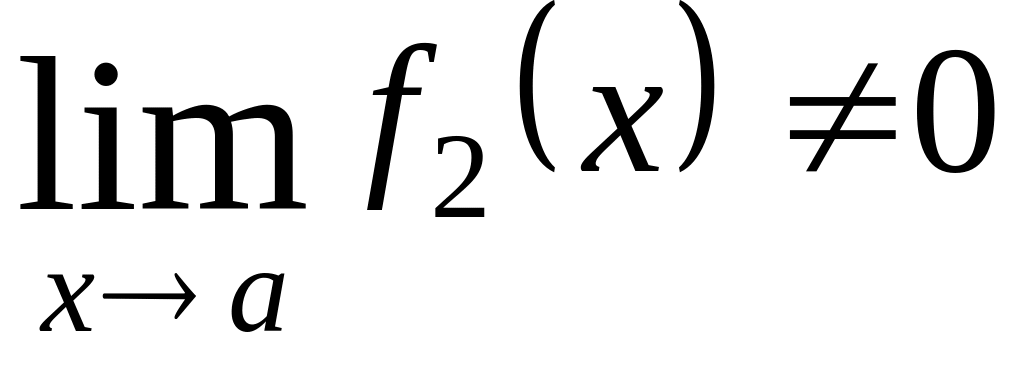
3.3. ПЕРША ВАЖЛИВА ГРАНИЦЯ

Наслідки: 1)

2)

3)

3.4. ДРУГА ВАЖЛИВА ГРАНИЦЯ

Наслідки: 1)

2)

ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ

Приклад 1.

Розкриття невизначеностей вигляду .

Розв’язування.

Для того щоб розкрити невизначеність такого виду, необхідно чисельник і знаменник дробу поділити на , - найбільший степінь чисельника і знаменника:

а)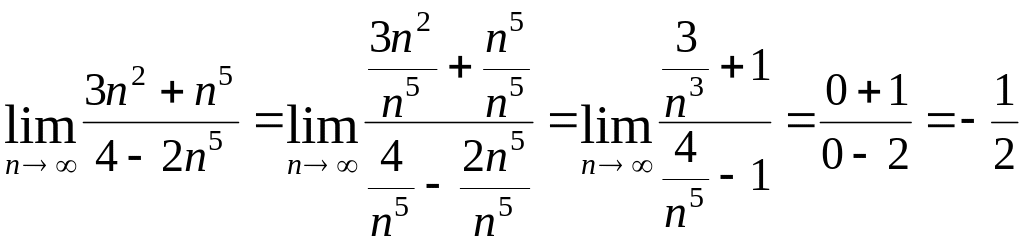

б)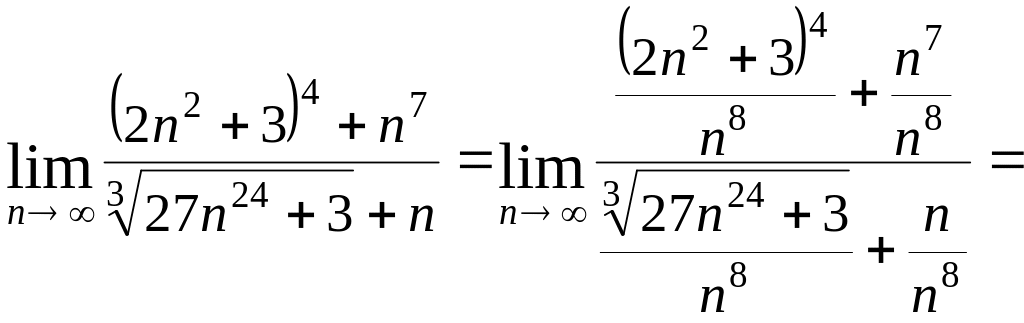

.

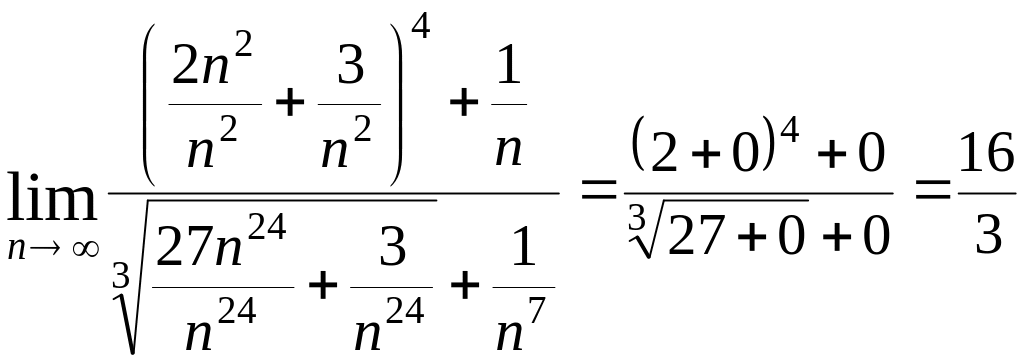Приклад 2.

Розкриття невизначеностей вигляду .

Розв’язування.

Для того щоб розкрити невизначеність такого виду необхідно чисельник і знаменник дробу розкласти на множники і скоротити множник, який прямує до 0.

При цьому використовуємо формули:

1. 

2. 

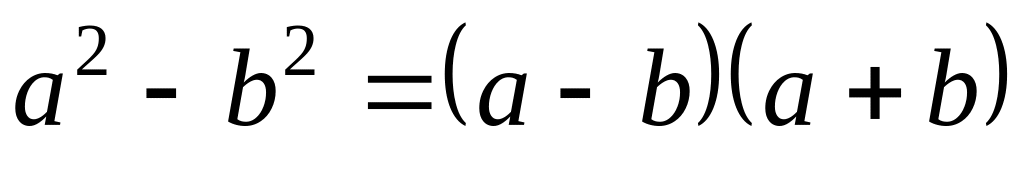
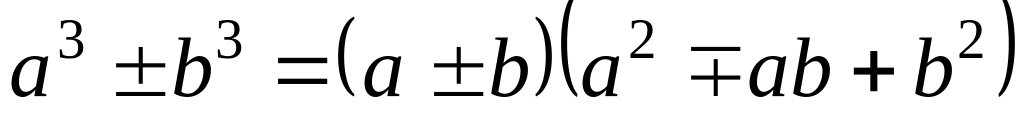
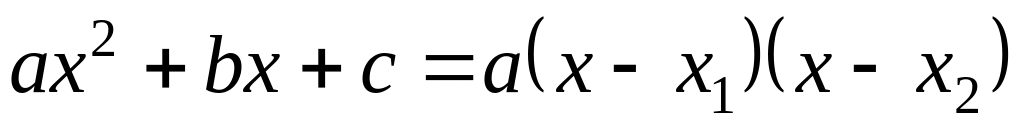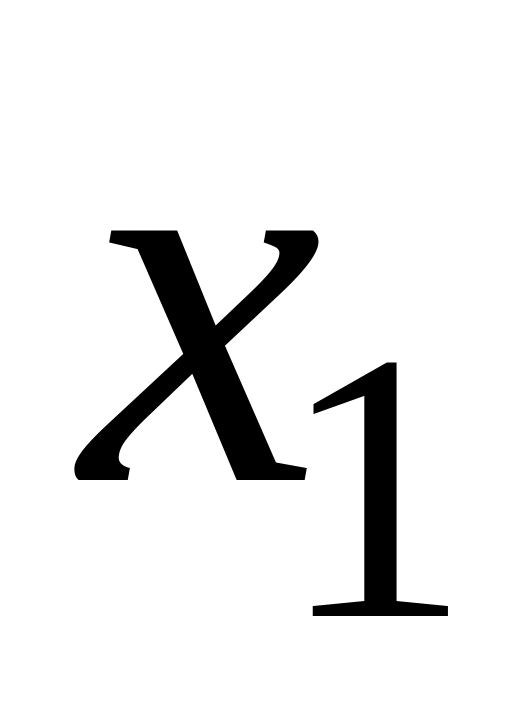3. , де і 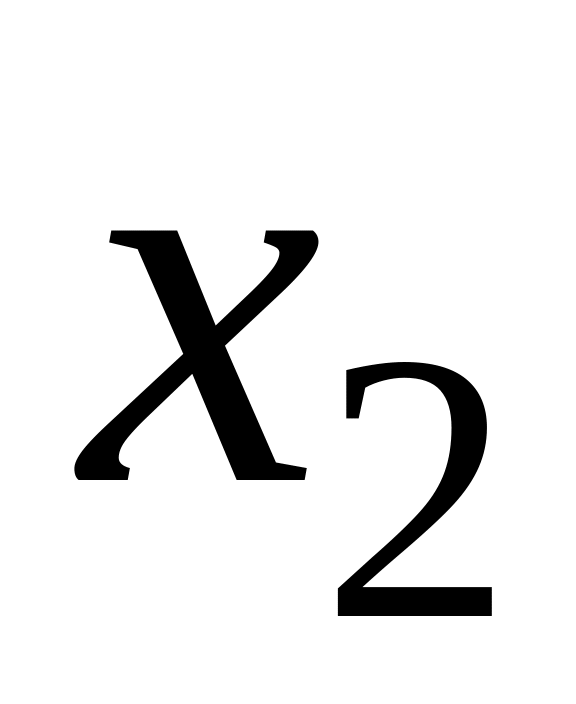- корені квадратного рівняння

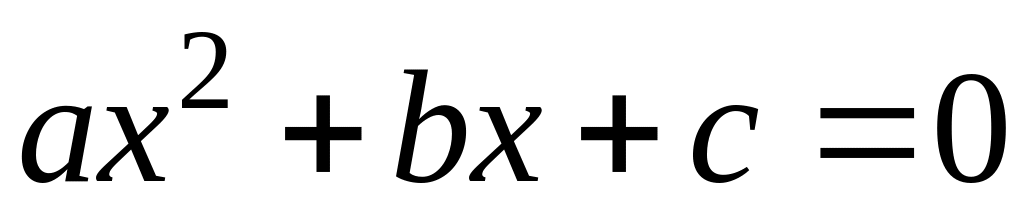
а)

Розкладемо чисельник і знаменник на множники:

Отже;

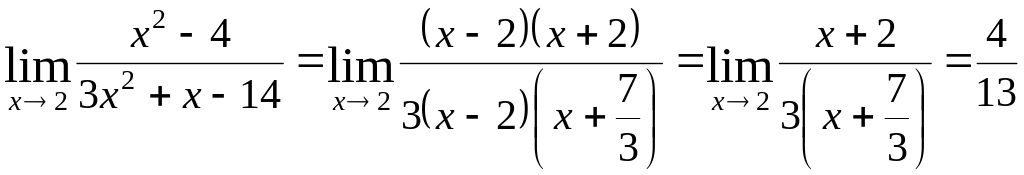
б)

Розкладемо чисельник і знаменник на множники:

Для того щоб розкласти чисельник на множники поділимо його на за правилом ділення многочленів:

- - - -

Таким чином,

Отже,

в) .

Позбудемось спочатку ірраціональності в численьнику; для цього чисельник і знаменник домножимо на спряжений вираз і скористаємося властивостями функцій, які мають границю

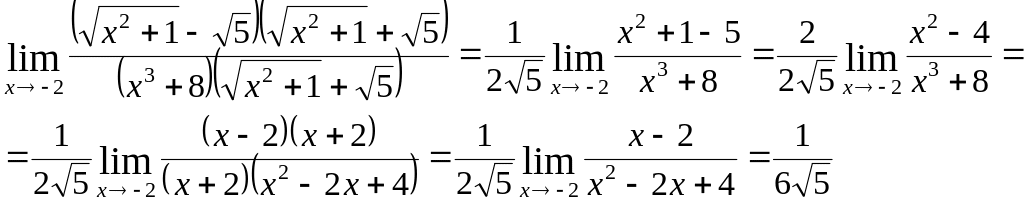
Приклад 3.

Застосування першої важливої границі:

а)

б)

Приклад 4.

Застосування другої важливої границі:

а)

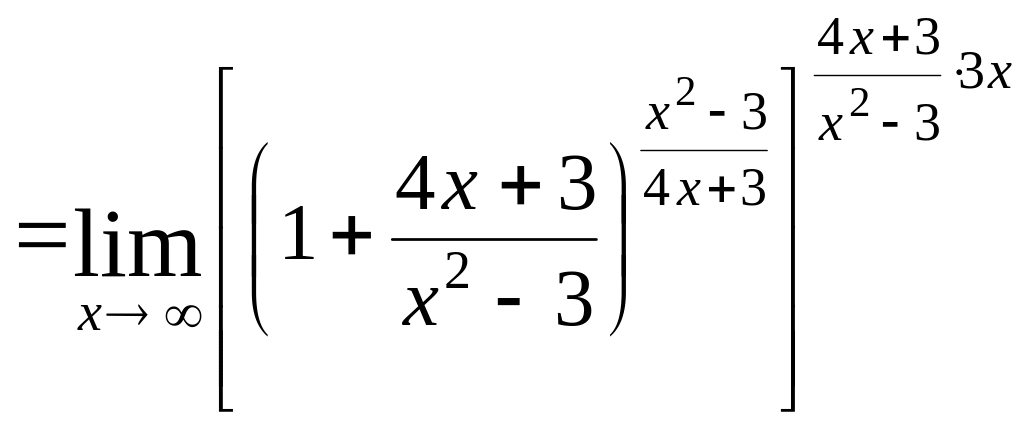
Границя виразу, що стоїть в квадратних душках, дорівнює . Оскільки - неперервна функція, то перейдемо до границі під знаком функції. Одержимо:

=

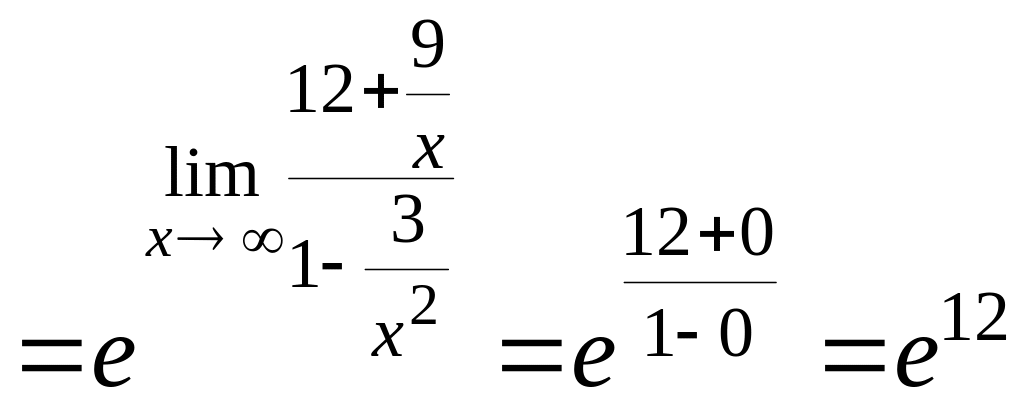
б)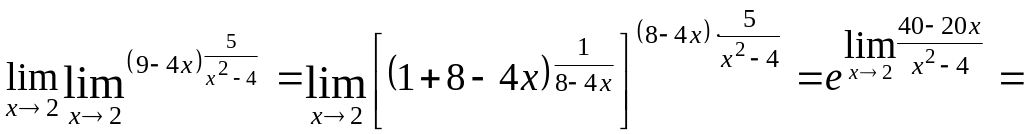 .