25. Классификация изолированных особых точек аналитической функции. Устранимая особая точка и разложение в ее окрестности аналитической функции.
Определение.
Особая точка
функции
называется изолированной, если в
некоторой окрестности этой точки функция
аналитическая (кроме самой точки) и не
имеет других особых точек.
Разложим функцию в ряд Лорана в окрестности изолированной особой точки. При этом возможны три случая:
Ряд Лорана не содержит членов с отрицательными степенями разности
.Содержит конечное число членов с отрицательными степенями разности .
Содержит бесконечное число членов с отрицательными степенями разности .
В зависимости от этих случаев производится классификация изолированных особых точек.
Ряд Лорана имеет вид:
,
,
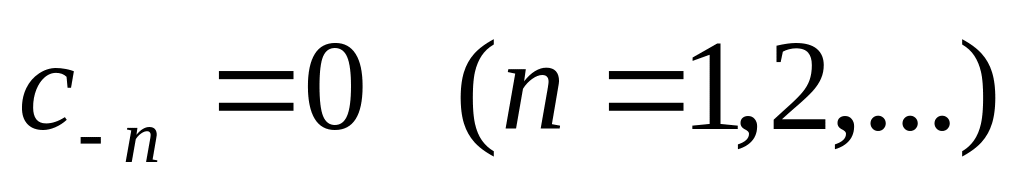то есть главная часть ряда в разложении
отсутствует.
Это разложение имеет место во всех точках некоторой окрестности точки . Правая часть равенства – степенной ряд является аналитической функцией при .
Поэтому,
если под
понимать сумму ряда при
,
то есть положить
,
то точка
будет правильной точкой
и разложение будет разложением функции
в ряд Тейлора. Точка
называется устранимой особой точкой.
.
Пример.
.
.
2.
Ряд Лорана содержит конечное число
членов с отрицательными степенями
разности
.
.
Точка
в этом случае называется полюсом порядка
функции
.
Если
,
полюс называется простым. Функцию
можно представить в виде
,
где
– аналитическая функция,
.
В
этом случае
.
Если
точка
полюс порядка
функции
,
то
,
где
– аналитическая функция, и
является нулем порядка
функции
.
Примеры.
1)
;
– полюс третьего порядка.
2)
– полюса первого порядка (простые).
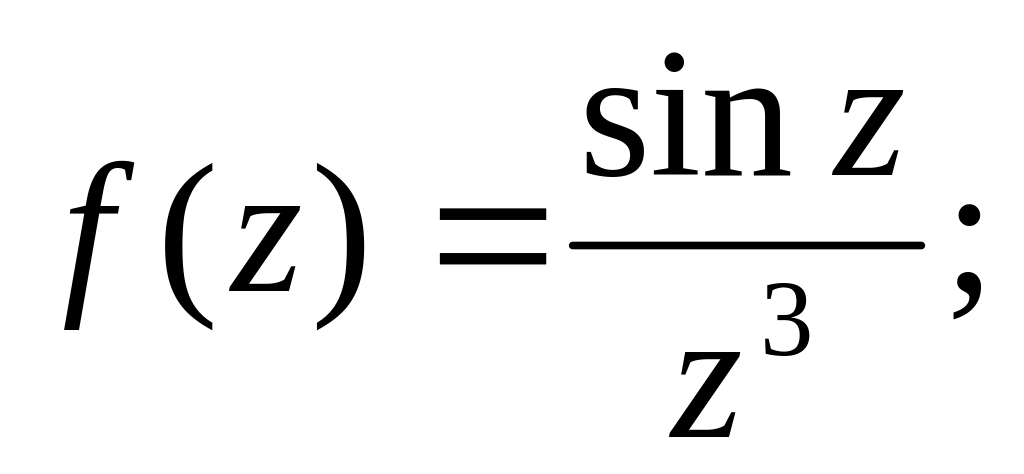– полюс
второго порядка.
.
Если ряд Лорана в окрестности особой точки содержит бесконечное число членов с отрицательными степенями , то точка называется существенно особой точкой.
В
этом случае
не существует (ни конечный, и бесконечный).
26. Классификация изолированных особых точек аналитической функции. Полюс порядка функции и ее разложение в окрестности полюса. Определение мероморфной функции.
Изолированные особые точки и их классификация
Определение. Особая точка функции называется изолированной, если в некоторой окрестности этой точки функция аналитическая (кроме самой точки) и не имеет других особых точек.
Разложим функцию в ряд Лорана в окрестности изолированной особой точки. При этом возможны три случая:
Ряд Лорана не содержит членов с отрицательными степенями разности .
Содержит конечное число членов с отрицательными степенями разности .
Содержит бесконечное число членов с отрицательными степенями разности .
В зависимости от этих случаев производится классификация изолированных особых точек.
Ряд Лорана имеет вид: , , то есть главная часть ряда в разложении отсутствует.
Это разложение имеет место во всех точках некоторой окрестности точки . Правая часть равенства – степенной ряд является аналитической функцией при .
Поэтому, если под понимать сумму ряда при , то есть положить , то точка будет правильной точкой и разложение будет разложением функции в ряд Тейлора. Точка называется устранимой особой точкой. .
Пример. . .
2. Ряд Лорана содержит конечное число членов с отрицательными степенями разности .
.
Точка в этом случае называется полюсом порядка функции . Если , полюс называется простым. Функцию можно представить в виде
,
где – аналитическая функция, .
В этом случае .
Если точка полюс порядка функции , то ,
где – аналитическая функция, и является нулем порядка функции .
Примеры.
1) ; – полюс третьего порядка.
2) – полюса первого порядка (простые).
– полюс второго порядка. .
Если ряд Лорана в окрестности особой точки содержит бесконечное число членов с отрицательными степенями , то точка называется существенно особой точкой.
В этом случае не существует (ни конечный, и бесконечный).