Общие задания

1. Изучить теоретический материал.

2. Выполнить практический раздел.

3. Используя задачи предыдущей лабораторной работы (№2) и их решения, необходимо: а) к прямой ЗЛП, решаемой симплексным методом, составить двойственную ЗЛП вручную; б) найти оптимальный план двойственной ЗЛП вручную и при помощи Поиска решений.

4. Провести анализ полученных результатов, сделать выводы (отразить в отчете).

5. Оформить отчет.

Контрольные вопросы

1. Что такое двойственная ЗЛП?

2. Каковы правила составления двойственной ЗЛП относительно прямой ЗЛП?

3. Каковы теоремы двойственности?

4. Как определить решение двойственной задачи из решения прямой?

5. Какие функции для работы с матрицами в табличном процессоре MS Excel вы знаете?

Лабораторная работа №4

Тема: Транспортная задача. Метод потенциалов.

Цель: Познакомиться с транспортными задачами; научиться составлять экономико-математическую модель транспортной задачи, строить первоначальный опорный план, научиться улучшать первоначальный опорный план и получать оптимальный план методом потенциалов и с помощью Поиска решения и в Mathcad.

Теоретический раздел Транспортная задача

В современных условиях большие транспортные расходы связаны с простоями в ожидании обслуживания на погрузочно-разгрузочных работах, порожними пробегами, встречными и нерациональными перевозками, затратами на бензин, техническое обслуживание и заработную плату водителей. В связи с этим необходимо решать задачи оптимального планирования перевозок грузов в коммерческой деятельности из пунктов отправления (баз, станций, фабрик, совхозов, заводов) в пункты назначения (магазины, склады) методами, позволяющими оптимизировать план по какому-либо экономическому показателю, например финансовых затрат или времени на перевозку грузов.

Для решения подобного рода задач в линейном программировании существуют специально разработанные методы, а задачи такого рода называются транспортными задачами (ТЗ).

Построение экономико-математической модели задачи

Имеется пунктов отправления (поставщиков) грузов:

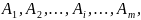
на которых сосредоточены запасы какого-либо однородного груза в объемах соответственно:

Величины определяют максимально возможные размеры вывоза груза с пунктов отправления. Суммарный запас груза поставщиков составляет . Кроме того, имеется пунктов назначения:

которые подали заявки на поставку грузов в объемах соответственно:

Суммарная величина заявок составляет . Стоимость перевозки одной единицы груза от поставщика к потребителю обозначим через (транспортный тариф), образующих матрицу транспортных издержек . В качестве критерия оптимальности выбираем суммарные издержки по перевозке грузов.

Тогда ТЗ формулируется следующим образом: необходимо составить оптимальный план, т.е. найти такие значения объема перевозок грузов от поставщиков к потребителям , чтобы вывести все грузы от поставщиков; удовлетворить заявки каждого потребителя и обеспечить минимальные транспортные расходы на перевозку груза.

Все исходные данные ТЗ можно записать в виде таблицы (табл. 4.1), которая называется транспортной:

Таблица 4.1

Пункты отправления	Пункты назначения						Запасы, ai
	В1	В2	…	Bj	…	Bn
A1	c11 x11	c12 x12	…	c1j x1j	…	c1n x1n		a1
A2	c21 x21	c22 x22	…	c1j x1j	…	c1n x1n		a2
…	…	…	…	…	…	…		…
Ai	ci1 xi1	ci2 xi2	…	cij xij	…	cin xin		ai
…	…	…	…	…	…	…		…
Am	cm1 xm1	cm2 xm2	…	cmj xmj	…	cmn xmn		am
Заявки, bj	b1	b2	…	bj	…	bn

Задача заключается в определении плана перевозок – матрицы , которая удовлетворяет следующим условиям:

И обеспечивает минимальное значение целевой функции

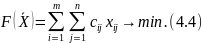
В таком виде экономико-математическая постановка ТЗ считается законченной.