
- •Приднестровский государственный универсистет им. Т.Г. Шевченко
- •Математическое моделирование в экономике
- •Содержание
- •Предисловие
- •Введение
- •Лабораторная работа №1
- •Теоретический раздел Методы линейного программирования
- •Общая задача линейного программирования (злп)
- •Постановка злп
- •Построение экономико-математической модели задачи
- •Переход от стандартной записи задачи к канонической
- •Примеры типовых задач
- •Надстройка «Solver» (Поиск решения)
- •Параметры средства Поиск решения
- •Отчеты поиска решения
- •Математический редактор Mathcad
- •Общие задания
- •Индивидуальные задания
- •Контрольные вопросы:
- •Лабораторная работа №2
- •Теоретический раздел Симплексный метод решения злп
- •Алгоритм симплексного метода
- •Примеры типовых задач
- •Симплексная таблица
- •Практический раздел
- •Общие задания
- •Контрольные вопросы
- •Лабораторная работа №3
- •Теоретический раздел Взаимодвойственные злп
- •Построение двойственной задачи
- •Правила построения двойственных задач
- •Теоремы двойственности
- •Соотношение переменных прямой и двойственной задач
- •Пример типовой задачи
- •Практический раздел
- •Общие задания
- •Контрольные вопросы
- •Лабораторная работа №4
- •Теоретический раздел Транспортная задача
- •Построение экономико-математической модели задачи
- •Построение опорного плана
- •Метод наименьшей стоимости (тарифов)
- •Метод северо-западного угла (диагональный)
- •Получение оптимального плана. Метод потенциалов
- •Алгоритм оценки оптимальности плана методом потенциалов
- •Примеры типовых задач
- •Практический раздел
- •Общие задания
- •Индивидуальные задания
- •Контрольные вопросы
- •Лабораторная работа №5
- •Теоретический раздел Теория игр
- •Основные понятия теории игр
- •Постановка игровых задач, методы и модели их решения
- •Принцип минимакса
- •Характерные оценки
- •Решение игр в смешанных стратегиях
- •Метод линейного программирования
- •Примеры типовых задач
- •Производственные стратегии фирмы
- •Платежная матрица
- •Практический раздел
- •Общие задания
- •Индивидуальные задания
- •Контрольные вопросы
- •Лабораторная работа №6
- •Теоретический раздел Инвестиционный портфель ценных бумаг
- •Оптимальный портфель инвестиций
- •Доходность портфеля ценных бумаг
- •Измерение риска портфеля ценных бумаг
- •Оптимизация портфеля ценных бумаг
- •Построение экономико-математической модели задачи
- •Практический раздел Оптимальный портфель инвестиций с максимальным доходом
- •Проценты доходности ценных бумаг и рынка
- •Оптимальный портфель инвестиций с минимальным риском
- •Общие задания
- •Индивидуальные задания
- •Контрольные вопросы
- •Лабораторная работа №7
- •Теоретический раздел Нелинейные модели
- •Задача управления запасами
- •Постановка задачи
- •Основные понятия и определения
- •Основная модель управления запасами. Модель Уилсона
- •Входные:
- •Выходные:
- •Построение экономико-математической модели задачи
- •Модель планирования экономичного размера партии
- •Построение экономико-математической модели задачи
- •Практический раздел
- •Общие задания
- •Индивидуальные задания
- •Контрольные вопросы
- •Лабораторная работа №8
- •Теоретический раздел Теория массового обслуживания
- •Определение характеристик и моделирование систем массового обслуживания Потоки событий
- •Простейшая одноканальная модель
- •Примеры типовых задач Анализ входного потока заявок
- •Анализ потока обслуживания заявок
- •Анализ одноканальной смо
- •Практический раздел
- •Общие задания
- •Индивидуальные задания
- •Контрольные вопросы
- •Список литературы
- •Приложение
- •Математическое моделирование в экономике
Симплексная таблица
План |
Базисные перменные |
Значения базисных переменных |
xн |
xв |
x1 |
x2 |
x3 |
x4 |
min |
I |
x1 |
3 |
0,5 |
1 |
1 |
0 |
0 |
0 |
3 |
x2 |
4 |
1 |
0,5 |
0 |
1 |
0 |
0 |
8 |
|
x3 |
1,5 |
-1 |
1 |
0 |
0 |
1 |
0 |
1,5 |
|
x4 |
2 |
0 |
1 |
0 |
0 |
0 |
1 |
2 |
|
|
0 |
-2 |
-3 |
0 |
0 |
0 |
0 |
|
|
II |
x1 |
1,5 |
1,5 |
0 |
1 |
0 |
-1 |
0 |
1 |
x2 |
3,25 |
1,5 |
0 |
0 |
1 |
-0,5 |
0 |
13/6 |
|
xв |
1,5 |
-1 |
1 |
0 |
0 |
1 |
0 |
- |
|
x4 |
0,5 |
1 |
0 |
0 |
0 |
-1 |
1 |
0,5 |
|
|
4,5 |
-5 |
0 |
0 |
0 |
3 |
0 |
|
|
III |
x1 |
0,75 |
0 |
0 |
1 |
0 |
0,5 |
-1,5 |
1,5 |
x2 |
2,5 |
0 |
0 |
0 |
1 |
1 |
-1,5 |
2,5 |
|
xв |
2 |
0 |
1 |
0 |
0 |
0 |
1 |
- |
|
xн |
0,5 |
1 |
0 |
0 |
0 |
-1 |
1 |
- |
|
|
7 |
0 |
0 |
0 |
0 |
-2 |
5 |
|
|
IV |
x3 |
1,5 |
0 |
0 |
2 |
0 |
1 |
-3 |
- |
x2 |
1 |
0 |
0 |
-2 |
1 |
0 |
1,5 |
2/3 |
|
xв |
2 |
0 |
1 |
0 |
0 |
0 |
1 |
2 |
|
xн |
2 |
1 |
0 |
2 |
0 |
0 |
-2 |
- |
|
|
10 |
0 |
0 |
4 |
0 |
0 |
-1 |
|
|
V |
x3 |
3,5 |
0 |
0 |
-2 |
2 |
1 |
0 |
|
x4 |
2/3 |
0 |
0 |
-4/3 |
2/3 |
0 |
1 |
|
|
xв |
1 1/3 |
0 |
1 |
4/3 |
-2/3 |
0 |
0 |
|
|
xн |
3 1/3 |
1 |
0 |
-2/3 |
4/3 |
0 |
0 |
|
|
|
10 2/3 |
0 |
0 |
2 2/3 |
2/3 |
0 |
0 |
|
Первый опорный план заносим в симплексную табл. 2.5, который не является оптимальным, поскольку в индексной строке находятся отрицательные коэффициенты (-2) и (-3). Затем, действуя в соответствии с изложенными выше правилами, переходим последовательно от одного плана к другому, пока не построим оптимальный план V, в котором в индексной строке отсутствуют отрицательные элементы.
Запишем оптимальный план:

Таким образом, для
получения максимального дохода от
дневной продажи краски
 тыс.
руб. предприятию необходимо выпускать
в сутки
тыс.
руб. предприятию необходимо выпускать
в сутки
 т краски
наружных работ и
т краски
наружных работ и
 т краски для
внутренних работ. В оптимальный план
вошли дополнительные переменные
т краски для
внутренних работ. В оптимальный план
вошли дополнительные переменные
 = 3,5 и
=
= 3,5 и
=
 ,
что свидетельствует о величине
недоиспользованных ресурсов третьего
и четвертого вида. Следует заметить,
что остальные ресурсы использованы
полностью, поскольку
,
что свидетельствует о величине
недоиспользованных ресурсов третьего
и четвертого вида. Следует заметить,
что остальные ресурсы использованы
полностью, поскольку
 .
.
Полученный
оптимальный план является невырожденным,
так как при расчете столбца di
отсутствуют одинаковые минимальные
значения отношений и все значения
базисных переменных в оптимальном плане
отличны от нуля. Кроме того, поскольку
в индексной строке в столбцах переменных
 ,
не вошедших в состав базисных, получены
не нулевые элементы, то оптимальный
план является единственным.
,
не вошедших в состав базисных, получены
не нулевые элементы, то оптимальный
план является единственным.
Пример 3. Рассмотрим применение симплексного метода с определением новых неотрицательных базисных переменных задачи на нахождение минимума целевой функции.
Фирма производит и продает диваны, софы и кресла, для декоративной отделки которых использует натуральную змеиную кожу, кожзаменитель и атлас. Расход каждого вида в метрах на каждое изделие приведен в табл. 2.6.
Таблица 2.6
Изделия |
Материалы, м2 |
Минимальный план производства, ед. |
||
Кожзаменитель |
Кожа |
Атлас |
||
Диван |
0,5 |
0,7 |
1 |
3 |
Софа |
0,3 |
0,2 |
0,8 |
6 |
Кресла |
0,4 |
0,7 |
- |
7 |
Себестоимость материалов, тыс. руб./ |
5 |
2 |
9 |
|
Сколько материала каждого вида необходимо приобрести фирме, чтобы выполнить минимальный план производства и минимизировать затраты?
Определим значение целевой функции

при следующих условиях-ограничениях:

Для построения первого опорного плана систему неравенств приведем к к канонической форме:

а целевую функцию представим в виде уравнения

Умножим все строки системы на (-1) и будем искать первоначальный опорный план:

Полагая, что
основные переменные
 ,
получим первый опорный план:
,
получим первый опорный план:

в котором базисные переменные равны:

Первый опорный план заносим в симплексную табл. 2.7, который не является допустимым, поскольку базисные переменные отрицательные. Для того. Чтобы определить новые неотрицательные базисные переменные используют также симплексный метод.
Таблица 2.7
План |
Базисные перменные |
Значения базисных переменных |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
I |
X4 |
-3 |
-0,5 |
-0,7 |
-1 |
1 |
0 |
0 |
X5 |
-6 |
-0,3 |
-0,2 |
-0,8 |
0 |
1 |
0 |
|
X 6 |
-7 |
-0,4 |
-0,7 |
0 |
0 |
0 |
1 |
|
|
0 |
5 |
2 |
9 |
0 |
0 |
0 |
|
|
0 |
-12,5 |
-2,86 |
- |
- |
- |
- |
|
II |
X4 |
4 |
-0,1 |
0 |
-1 |
1 |
0 |
-1 |
X 5 |
-4 |
-0,19 |
0 |
-0,8 |
0 |
1 |
-0,29 |
|
X2 |
10 |
0,57 |
1 |
0 |
0 |
0 |
-1,43 |
|
|
-20 |
3,86 |
0 |
9 |
0 |
0 |
2 ,86 |
|
min |
0 |
-20,3 |
- |
-11,25 |
- |
- |
-10 |
|
III |
X4 |
18 |
0,55 |
0 |
1,8 |
1 |
-3,5 |
0 |
X6 |
14 |
0,65 |
0 |
2,8 |
0 |
-3,5 |
1 |
|
X2 |
30 |
1,5 |
1 |
4 |
0 |
-5 |
0 |
|
|
-60 |
2 |
0 |
1 |
0 |
10 |
0 |
1. Проверка критерия оптимальности. Происходит так же как в описанном ранее алгоритме, т.е. определяется допустимость плана.
2. Определение новых свободной и базисной переменных. Из отрицательных значений базисных переменных выбираем наибольший по абсолютной величине, что и определяет ведущую строку, которая показывает, какая переменная на следующей итерации перейдет из базисных в свободные.
Затем элементы индексной строки делим на элементы того же знака ( ) ведущей строки. Результаты заносим в отдельный столбец . Столбец, соответствующий минимальному значению , является ведущим. Он и определяет переменную , которая на следующей итерации выйдет из свободных членов и станет базисной (обмен).
Элемент, находящийся на пересечении ведущих столбца и строки, так же называют разрешающим.
Далее выполняется пересчет симплексной таблицы методом прямоугольника и заполняется план II. Если он окажется псевдопланом, то далее по алгоритму отыскиваются новые значения базисных переменных. Алгоритм повторяется дл тех пор, пока все значения базисных переменных не станут положительными. После чего оптимальный план находится обычным способом, если в этом есть необходимость.
В нашем примере план I в симплексной таблице является псевдопланом, поэтому определяем ведущие строку и столбец.
Среди отрицательных значений базисных переменных наибольший по модулю является x6 = -7. Ведущей будет 3-ая строка, а переменную x6 следует вывести из базиса.
Минимальное
значение
 соответствует 2-му столбцу, т.е. переменную
x2
необходимо ввести в базис. На пересечении
ведущих строки и столбца находится
разрешающий элемент (РЭ), равный (-0.7).
соответствует 2-му столбцу, т.е. переменную
x2
необходимо ввести в базис. На пересечении
ведущих строки и столбца находится
разрешающий элемент (РЭ), равный (-0.7).
Далее выполняем пересчет симплексной таблицы методом прямоугольника и заполняем план II, который является псевдопланом, поэтому определяем ведущие строку и столбец.
Среди отрицательных значений базисных переменных наибольшим по модулю является x5 = -4. Ведущей будет 2-ая строка, а переменную x5 следует вывести из базиса.
Минимальное
значение
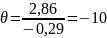 соответствует 6-му столбцу, т.е. переменную
x6
необходимо ввести в базис. На пересечении
ведущих строки и столбца находится
разрешающий элемент (РЭ), равный (-0.29).
соответствует 6-му столбцу, т.е. переменную
x6
необходимо ввести в базис. На пересечении
ведущих строки и столбца находится
разрешающий элемент (РЭ), равный (-0.29).
Далее выполняем пересчет симплексной таблицы методом прямоугольника и заполняем план III, который является допустимым, т.к. в базисном столбце все элементы положительные. Переходим к основному алгоритму симплекс-метода.
Среди значений индексной строки нет отрицательных. Поэтому план III является оптимальным, так как все коэффициенты в индексной строке 0.
Оптимальный план можно записать так:

Следовательно, необходимо приобрести для отделки только натуральную кожу в количестве = 30 м2, а другие материалы приобретать не следует. При этом у предприятия затраты минимальны = 60 тыс. руб.
В оптимальном плане среди базисных переменных находятся дополнительные переменные и . Это указывает на то, что изделий первого вида (диваны) произведено больше, чем указано в минимальном плане на 18 ед., а изделий третьего вида (кресла) – на 14 уд.
В индексной строке
оптимального плана в столбцах переменных
 ,
не вошедших в состав базисных, получены
ненулевые элементы, поэтому оптимальный
план ЗЛП является единственным.
,
не вошедших в состав базисных, получены
ненулевые элементы, поэтому оптимальный
план ЗЛП является единственным.



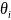 min
min