22. Интеграл с переменным верхним пределом

Если ф-ия y= f(x) интегрируема на отрезке [a;b], то, очевидно, она интегрируема также на произвольном отрезке [a;x] вложенном в [a;b].

Определим : Ф(х) = , где xϵ [a;b] , а ф-ия Ф(х) наз-ся определенным интегралом с переменным верхним приделом.

Геометрический смысл интеграла с переменным верхним пределом

Пусть f(x)≥0 на [a;b]. Тогда значение ф-ии Ф(х) в точке х равно площади S(x) под кривой y=f(x) на [a;b].

Свойства ф-ии Ф(х)

Теорема 3.1

Если ф-ия f(x) непрерывна на отрезке[a;b], то ф-ия Ф(х) также непрерывна на этом отрезке

Теорема 3.2

Производная определенного интеграла по переменному верхнему пределу равна подынтегральной ф-ии, в которой переменная интегрирования заменена этим пределом, т.е.

Ф(х)= (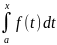 )’= f(x)

Это означает, что опр. Интеграл с переменным верхним пределом есть одно из первообразных подынтегральной функции.

23. Замена переменной и интегрирование по частям в опр. Интеграле

Пусть для вычисления Интеграла от непрерывной ф-ии f сделана подстановка x=ϕ(t)

Теорема 4.1

1. Ф-ия x=ϕ(t) и ее производная непрерывны при tϵ{α;β}

2)Множеством значений ф-ии x=ϕ(t) при

tϵ {α;β} явл-ся среда [a;b]

2. ϕ(α)=a, ϕ(β)=b то

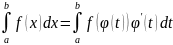(3.3)

Формула 3.3 наз-ся формулой замены переменной в опр. Интеграле

Замечание:

1. При вычислении опр интеграла методом подстановки возвращаться к старой переменной не требуется

2. Часто вместо подстановки x=ϕ(t) применяют подстановку t=g(x)

3. Не следует забывать менять пределы интегрирования при замене переменных

Интегрирование по частям

Если ф-ия u= u(x)и v=v(x) имеют непрерывные производные на отрезке [a;b] , то имеет место формула

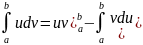( 3.4)

Фомула (3.4) наз-ся формулой интегрирования по частям для определения интеграла

24. Свойства интегралов от четных и нечетных функций по симметричному относительно 0 промежутку

Пусть ф-ия f(x) непрерывна на[a-;a], симметрична относительно точке х=0

1.f(x)- четная на [-a;a]

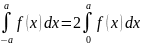
2. .f(x)-- нечетная на отрезке[-a;a]

25. Вычисление площадей плоских фигур с помощью определенного интеграла

Вычисление площадей плоских фигур основано на геометрическом смысле определенного интеграла

1 пусть ф-ия y=f(x)≥0 неотрицательна и непрерывна на [a;b] Тогда по геометрическому смыслу определённого интеграла площадь под кривой y=f(x) численно равна определенному интегралу.

Если криволинейная трапеция лежит ниже оси Ох y=f(x)≤0, то ее площадь может быть найдена по формуле:

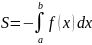
2 Площадь фигуры ограниченной кривыми

И и Переменными x=a, x=b при условии

S(заштрих) вычисляется по формуле

Рассмотрим фигуру

Для того чтобы найти ее площадь следует [a;b]разбить на частные отрезки на которых ф-ия f(x) сохраняет знаки и применить уже известные формулы

Если плоская фигура имеет «сложную» форму, то прямыми, пересекающими оси Оу, ее следует разбить на части так, чтобы можно было применить уже известные формулы.

3 Если криволинейная трапеция ограничена прямыми y=c и y=d , осью Оу и непрерывной кривой x=ϕ(y)≥0 , то ее площадь находится по формуле

S=

4. Если криволинейная трапеция ограничена кривой, заданной параметрически

tϵ [α;β)

Прямыми x>a, x=b и осью Ох, то ее площадь вычисляется по формуле

S=|

Где α и β определяются из равенств

X(α)=a, x(β)=b