7. Таблица интегралов
1. 0*du=С.
2. 1*du= u+С
3.
udu=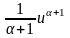
+С,
(1)
4.
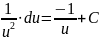
5.
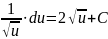
6.
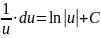
7.
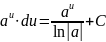
8.
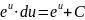
9.
sinu
du=
–соsu+С
10. соsudu=sinu+С
11.
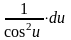=tgu+С
12.
=
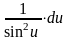-сtgu+С
13.
14.
15.
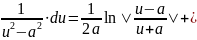C
16.
8. Интегрирование по частям в неопределенном интеграле
Формула
,
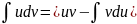где u=u(x)
и v=v(x)
– дифференцир.ф-ции, называется формулой
интегрирования по частям. Этот метод
целесообразно применять, если
более прост в вычислении, чем интеграл
.
Некоторые типы интегралов, которые можно вычислить методом интегрирования по частям:
1.
Интегралы вида
,
,
,
,
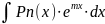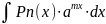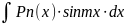где Pn(x)
– многочлен, m
– число. Здесь поладают: u
= Pn(x).
За dv
обозначают остальные сомножители.
2.
Интегралы
вида
,
,
,
,
.
Pn(x)dx
= dv,
за u
обозначают остальные сомножители.
3.
Интегралы
вида
,
,
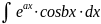где a
и b
– некотор.числа, за u
можно принять ф-цию
.
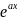9. Интегрирование заменой переменной в неопределенном интеграле. Примеры подстановок.
Метод
замены переменной (подстановки) состоит
в преобразовании интеграла
в другой интеграл
,
который вычисляется проще, чем исходный.
Теорема:
Пусть ф-ция
определена и дифференцируема на некотором
множестве T
и пусть x
– множество значений этой ф-ции, на
котором определена ф-ция f(x).
Тогда, если на множестве x
ф-ция f(x)
имеет первообразную, то на множестве T
справедлива формула:
Эта
формула также называется формулой
замены переменных в неопределенном
интеграле. После нахождения интеграла
правой части этого равенства следует
перейти от новой переменной интегрирования
t
назад к переменной x.
Иногда целесообразно подбирать
подстановку в виде
,
тогда:
.
Примеры
подстановок:
1)
Универсальная тригонометрическая
подстановка: t=tg(x/2),
тогда
,
,
,
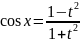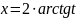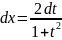2)
Интегралы типа
:
Для вычисления интегралов такого типа
используют след.приемы:
1.
Подстановка sinx=t,
если n
– целое положительное нечетное число.
2.
Подстановка cosx=t,
если m
-- целое положительное нечетное число.
3.
Формулы понижения порядка:
,
,
sinx*cosx=1/2*sin2x.
10. Интегрирование простейших рациональных дробей
,
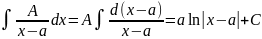
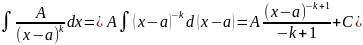k≥2,
kϵN
?,
k≥2,
kϵN
Где A, a, M, N, p, q – действительные числа.
В
пунктах 3 и 4 в знаменателе выделяем
полный квадрат и делаем подстановку
.
Теорема
Всякую правильную рациональную дробь, знаменатель которой разложен на множители
можно представить
(и при том в единственном образе) в виде
следующей суммы простейших дробей:
(1)
Для нахождения неопределенных коэффициентов в равенстве (1) можно применить два метода.
Метод неопределенных коэффициентов
В правой части равенства (1) приведем дроби к общему знаменателю Q(x), в результате получим тождество
,
где S(x)
– многочлен с неопределенными
коэффициентами.Так как в полученном тождестве знаменатели равны, то тождественно равны и числители, т.е. P(x)≡S(x) (2)
Приравнивая коэффициенты при одинаковых степенях в обеих частях тождества (2), получим систему линейных уравнений, из которых и определим искомые коэффициенты
Метод отдельных значений аргумента: после получения тождества (2) аргументу х придают конкретные значения столько раз, сколько неопределенных коэффициентов (обычно полагают вместо х значения действующих корней многочлена Q(x))