42. Метод вариации произвольных постоянных.

Рассмотрим ЛНДУ . Его общим решением является функция .

Частное решение уравнения (4.1) можно найти ,если известно общее решение у соответствующего однородного уравнения методом вариации произвольных постоянных ( методом Лагранджа).

Пусть - общее решение уравнения (4.2)

Заменим в общем решении постоянные неизвестными функциями и подберем их так, чтобы функция

была решением уравнения (4.1).

Подберем функции так, чтобы

Тогда

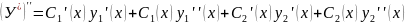
Подставляем выражение для У*, (У*)’ , (У*)’’ в уравнение (4.1) получим:

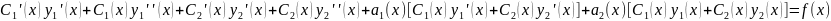
Или

Поскольку 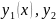(x) – решения уравнения (4.2.),,, то выражения в квадратных скобках равны 0, а потому

Таким образом, функция

будет частным решением уравнения (4.1),если функции удовлетворяют системе уравнений:

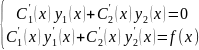(4.3)

Определитель системы:

Так как это определить Вронского для фундаментальной системы частных решений уравнения (4.2).

Потому система (4.3) имеет единственное решение:

где функции некоторые функции от x.

Интегрируя эти функции, находим , а затем составляем частное решение уравнения.

43.Интегрирование лоду n-го порядка с постоянными коэффициентами.

Задача нахождения общего решения ЛОДУ n-го порядка с постоянными коэффициентами

Где 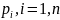– числа ,решается аналогично случаю уравнения второго порядка с постоянными коэффициентами .

Частное решение уравнения также ищем в виде

Характеристическим для уравнения (3.5) является алгебраическое уравнение n-го порядка вида

Уравнение (3.6) имеет как известно n корней ( в их числе могут быть комплексные). Обозначим их через

1. Все корни уравнения (3.6) действительны и различны. Тогда общее решение уравнения записывается в виде

2. Все корни характеристического уравнения действительны, но не все различны,т.е. есть корни имеющие кратность m > 1, тогда каждому простому корню k соответственно одно частное решение вида , а каждому корню k ‘ кратности m > 1 соответствует m частных решений.

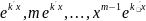
3. Среди корней уравнения есть комплексно сопряженные корни. Тогда каждой паре α±βi простых комплексно-сопряженных корней соответствует два частных решения

А каждой паре α’ ± β’i корней кратность m >1 соответствуют 2m частных решений вида

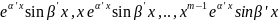
44. Лнду. Теорема о структуре общего решения.

Уравнение вида

где 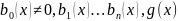– заданные функции ( от х), называются линейными. Если g(x)≠0, то уравнение называется неоднородным.

Рассмотрим ЛНДУ второго порядка

Где заданные непрерывные на промежутке (a;b) функции.

Если f(x) = 0, то уравнение

- называется соответствующим ему однородным уравнением.

Теорема (4.1) О структуре общего решения ЛНДУ

Общим решением уравнения (4.1) является сумма его произвольного частного решения и общего решения соответственно однородного уравнения (4.2) т.е.

45. Теорема о наложении решений лнду

Если правая часть уравнения

Представляет собой сумму двух функций:

, а - частные решения следующих уравнений

соответственно, то функция является решением данного уравнения.