1. Понятие фнп. Линии уровня.

Если каждой упорядоченной паре чисел (x;y) из некоторого числового множества D={(x;y)} поставлено в соответствии согласно некоторому правилу f число z из множества Z, то говорят, что на множестве D задана функция двух переменных z=f(x;y) При этом переменные x и y называются независимыми переменными или аргументами множества D={(x;y)} называется областью определения, а множество Z={f(x;y)|(x;y) ∈D} – множеством значений функции. Областью определения может быть вся плоскость ОХУ или её часть, ограниченная некоторыми линиями. Линию, ограничивающую область, называют границей области. Точки области, не лежащие на границе, называются внутренними. Область, состоящая из одних внутренних точек, называется открытой. Область с присоединенной к ней границей называется замкнутой, обозначается D. Примером замкнутой области является круг с окружностью. Значение функции z=f(x;y) в точке 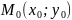обозначают и называют частным значением функции. Графиком функции z=f(x;y) называется поверхность, образованная множеством точек пространства с координатами (x;y;f(x;y)) для всех точек (x;y) ∈ D Функция двух переменных как и функция одной переменной может быть задана разными способами: таблицей, графиком, аналитически. Величина u называется функцией n переменных 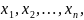если каждой совокупности ( ) переменных из каждой области n-мерного пространства соответствует определенное значение u, что записывается: u=f( )

Линией уровня функции z=f(x;y) называется множество всех точек плоскости ОХУ, в которых функция z принимает постоянное значение, т.е. f(x;y)= С, где С-постоянная. Число С в этом случае называется уровнем. Построение линии уровня оказывается более легкой задачей, чем построение графиков самих функций.

2. Частные производные фнп. Необходимые и достаточные условия дифференцируемости фнп

Частным приращением функции z=f(x;y) по независимой переменной х, соответствующим приращению , называется разность

Частным приращением функции z=f(x;y) по независимой переменной y, соответствующим приращению переменной y, называется разность

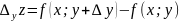
Полным приращением функции z=f(x;y) соответствующим приращениям аргументов и , называется разность

Частной производной первого порядка функции нескольких переменных по одной из этих переменных называется предел отношения соответствующего частного приращения функции к приращению данной переменной, когда последняя стремится к нулю. Для функции двух переменных z=f(x;y) по определению частная производная по x равна: 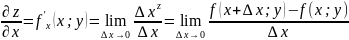Частная по y равна:

При нахождении частной производной пользуются правилами дифференцирования функции одной переменной, считая все другие аргументы постоянными. Частными производными второго порядка функции z=f(x;y) называются частные производные, если они существуют от её частных производных первого порядка.

Обозначение:

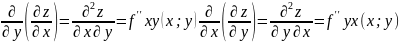
Аналогично определяются и обозначаются частные производные третьего и высшего порядков. Частные производные называются смешанными производными.

Необходимое условие диф-ости ф-ции. Если ф-ция z=f(x;y) диф-ема в точке М, то она непрерывна в этой точке, имеет в ней частные производные причем Тогда формула нахождения частных производных F(x;y;z)=0 имеет вид:

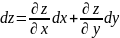
Достаточное условие дифференцируемости. Пусть существуют  для функции   непрерывной в  для функции m переменных. Тогда   непрерывна в  .