1. Компоненты САПР, основные концепции

2. САПР и ГИС: отличие, сходство, единство

3. Структура программного обеспечения САПР

4. Аппаратное обеспечение САПР

5. Ввод информации в САПР

6. Графические библиотеки в САПР

7. Окна и видовые экраны САПР

8. Основные примитивы САПР (на прим. AutoCAD)

9. Настройка параметров чертежа

10. Системы координат

11. Базовые функции черчения на примере Autocad

12. Управление объектной привязкой

13. Функции аннотирования ( простановка размеров, примечания)

14. Вспомагательные и дополнительные функции ( на примере express, toolpac)

15.Предсавление кривых в САПР и работа с ними

16. Кривые Безье

17. Интерполяционные кривые.

18. Цифровые модели местности

19. Регулярные ЦММ

20. Методы построения цифр. моделей местности и их точность

21. Математические модели местности

22. Пространственная триангуляция Делоне

23. Задача построение сети неперекрывающихся треугольников

24. Триангуляция Делоне.

25. Полиномиальные методы

26. Мультиквадриковый способ аппроксимации топогр. поверхн.

27.Методы Kriging

28. метод Inverse Distance.

29.Задачи, решаемые с использованием цифр.математич. моделей

30.Применение цифр. модел. местн. в автоматизир.сист. различн. назначения

31. Современные технологии сбора и обработки топогр. информаци

32. Обработка данных в программном комплексе Credo

33. Построение цифровой модели рельефа по растровой основе

34. Полуавтоматическая векторизация на примере Spotlight.

35. Построения регулярных координатных сеток в GoldenSoft.Surfer

36. Оценка точности постр/ регулярной сетки в Golden Soft. Surfer

37. Использование Faults and Breaklines в Golden Software Surfer.

38. Отображение полученных моделей в Golden Software Surfer.

39. Операции с поверхностями в Golden Software Surfer.

40. Подсчёт объёмов земл. работ котлованов, траншей и насыпей.

41. Площадное камеральное проектирование.

42. Картограмма земляных работ.

43. Проектирование горизонтальной площадки

44. Расчёт объёмов по триангуляции Делоне.

45. Расчет обьемов по регулярной модели

46. Формулы Симпсона для расчета объемов

47. Расчет объемов по регулярной модели в Surfer

48. Оценка точности вычисления объема в Surfer

13. Функции аннотирования ( простановка размеров, примечания)

К аннотациям относятся примечания, поясняющие обозначения других типов, а также объекты, обычно используемые для добавления информации к чертежу.

Примеры аннотаций

• Примечания и метки

• Таблицы

• Размеры и допуски

• Штриховки

• Метки-идентификаторы

• Блоки

Типы объектов, которые можно использовать при создании аннотаций

• Штриховки

• Текст (однострочный и многострочный)

• Таблицы

• Размеры

• Допуски

• Выноски и мультивыноски

• Блоки

• Атрибуты

Нанесение размеров является важным этапом в разработке конструкторской документации.

Размеры можно создавать для разных типов объектов, которые могут быть ориентированы разным образом. Существуют следующие основные типы нанесения размеров.

• Линейный

• Радиальный (радиус, диаметр, с изломом)

• Угловой

• Ординатный

• Длина дуги

Линейные размеры могут быть горизонтальными, вертикальными, параллельными, повернутыми, базовыми или в виде цепей. Некоторые примеры приведены на чертеже.

Примечания

Текст можно создать различными способами. Более короткие фрагменты выполняются с помощью однострочного текста. Для длинных надписей с форматированием используется многострочный текст (мтекст).

Несмотря на то что при нанесении надписей применяется текущий стиль текста, который определяет шрифт и параметры текста, существует несколько способов настройки внешнего вида текста. Существуют инструменты для масштабирования и выравнивания текста, поиска и замены текста, а также для проверки на наличие орфографических ошибок.

Текстовые надписи, используемые в размерах и допусках, выполняются с помощью команд, предназначенных для нанесения размеров. Многострочный текст может применяться и в выносках.

14. Вспомагательные и дополнительные функции ( на примере express, toolpac)

Инструменты Express Tools приложения AutoCAD содержат библиотеку инструментов повышения производительности, предназначенных для расширения функциональных возможностей AutoCAD.

Они просты в использовании, их легко интегрировать в пользовательские меню и панели инструментов. Они охватывают широкий диапазон функций, включая нанесение размеров, построение чертежа, а также выбор и изменение объектов.

Инструменты Express Tools приложения AutoCAD устанавливаются в процессе стандартной установки AutoCAD.

15.Предсавление кривых в сапр и работа с ними

Для каждого криволинейного ребра в компьютере хранится либо уравнение кри­вой, либо эквивалентные характеристические параметры.

Уравнения кривых могут быть разделены на два основных типа. К первому типу относятся параметрические уравнения, описывающие связь координат х, у и z точки кривой с параметром. Ко второму типу относятся непараметрические уравнения, связывающие координаты х, у и z некоторой функцией.

Кривая, отображаемая на экране, в действительности представляет собой набор коротких отрезков. Поэтому постоянно возникает необходимость вычислять координаты точек кривой, находящихся на равном расстоянии друг от друга. Это называется вычислением кривой (cuive evaluation).

Чаще всего для описания кривых, используемых в программах CAD, использу­ются уравнения третьего порядка, потому что они обладают важным свойством: две кривые, описываемые такими уравнениями, могут быть соединены таким образом, что вторые производные в точке соединения будут равны друг другу. Это означает, что кривизна в точке соединения остается постоянной, отчего две кривые кажутся одним целым. Ту же непрерывность можно получить и для кри­вых более высоких порядков, однако работа с ними требует интенсивных вычис­лений.

Безье предложил новую форму уравнения кривой и использовал ее в систе­ме поверхностного моделирования . Эта кривая получила назва­ние кривой Безье (Bezier curve). Она строится по вершинам многоугольника, за­ключающего ее в себе. Вершины сопрягаются соответствующими функциями. Безье выбрал функции сопряжения таким образом, чтобы получающаяся кривая удовлетворя­ла следующим требованиям.

• Кривая проходит через первую и последнюю вершины многоугольника.

• Направление вектора касательной в первой точке кривой совпадает с направ­лением первого отрезка многоугольника. Аналогичным образом, по­следний отрезок многоугольника определяет направление касательной в ко­нечной точке кривой.

• Производная степени n в начальной (или конечной) точке кривой определя­ется положением первых (или последних) n + 1 вершин многоугольника. Это свойство очень удобно при соединении двух кривых Безье, если требуется удовлетворить требованию непрерывности высших производных в точке со­единения. Вообще говоря, второе свойство есть частный случай данного свой­ства.

При изменении порядка вершин многоугольника на противоположный полу­чается та же самая кривая.

Задавшись этими требованиями, Безье выбрал в качестве функций сопряжения полином Бернштейна:

(1)

где

Если функцию сопряжения (1) применить к вершинам многоугольника, по­лучается уравнение кривой Безье:

(2)

где Р, — радиус-вектор n-й вершины. Вершины многоугольника называются за­дающими (control vertices), как и сам многоугольник (control polygon). Из форму­лы (2) видно, что для кривой, заданной n + 1 точками, максимальная степень будет 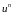. Таким образом, степень кривой Безье определяется количеством задаю­щих точек.

Рис. 4.1. Кривые Безье различных степеней

Интерполяционные кривые

чертежники рисуют кривые интуитивным методом. Они ставят на бумаге несколько точек в соответствии со своим представлением о форме кривой, а затем соединяют их плавной линией при помощи средства, называемого сплайном (spline). Так же и в САПР: конструктор указывает точки, а система строит по ним интерполя­ционную кривую, которую и отображает. Уравнение интерполяционной кривой сохраняется для последующей работы с ней. Можно создать кривую, непосред­ственно указав задающие точки кривой Безье или В-сплайна. Возможность стро­ить интерполяционные кривые по точкам очень полезна, если геометрическая модель создается по существующей физической модели.